Circle covers square 1

If the red and blue areas in each square are equal, they must each be half of the square. Let $A$ be the area of the square. Then we have $\frac{1}{4}\pi R^2 = \frac{A}{2}$ and $\pi r^2 = \frac{A}{2}$ . So $\begin{aligned} \frac{1}{4}\pi R^2 &= \pi r^2 \\ \frac{R^2}{r^2} &= 4 \\ \frac{R}{r} &= \boxed{2} \end{aligned}$

The larger circle, if completed, would cover 4 times the area, so it must have twice the radius of the smaller one.

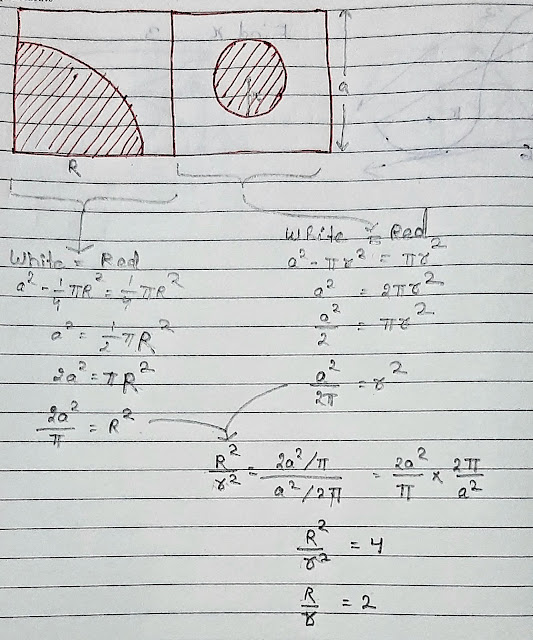
Assume that the area enclosed by each square is $2x$ . Then, the area covered by the circle of radius $R$ is $\frac{1}{4}\pi R^{2}=x$ . Solving for $R$ , we get $R=\sqrt{\frac{4x}{\pi }}=2\sqrt{\frac{x}{\pi }}$ . The area covered by the circle of radius $r$ is $\pi r^{2}=x$ . Solving for $r$ , we get $r=\sqrt{\frac{x}{\pi }}$ . As you can see, $R=2r$ , so therefore $\frac{R}{r}=2$ .

Boiling water solution

solution

Let a be the side of square. Then: $a^2-\frac{\pi R^2}{4} = a^2-\pi r^2$

$\frac{R^2}{r^2} = 4$

$\frac{R}{r} = 2$

Using area of sector formula; Area of quarter = 1/2 (R^2 θ) =1/4 (π R^2) Area of circle = π r^2

Let S be the side of a square. Then s^2 -(1/4) pi R^2 = S^2 = pi*r^2, R^2/4 = r^2, R/2 = r, R/r = 2

If the areas are equal, if the entire area was one that would mean the quarter circle radius is .5. That means the smaller full circle has a radius of .25 and .5/.25=2

Choose any positive number you want for "R".

$PinkCircleArea = Π*R^2$ ;

$PinkArea = PinkCircleArea / 4$ ;

$r = \sqrt{PinkArea / Π}$ ;

And $R/r$ always results in "2".

Area of the left sided quarter circle is A= 1/4x πR^2 and area of small circle on Rt side is πr^2 . Since both areas are equal therefore

1/4 X πR^2 = πr^2 => R^2/ r^2 = 4/1 => R/ r = 2