Circle geometry by Guy Fox
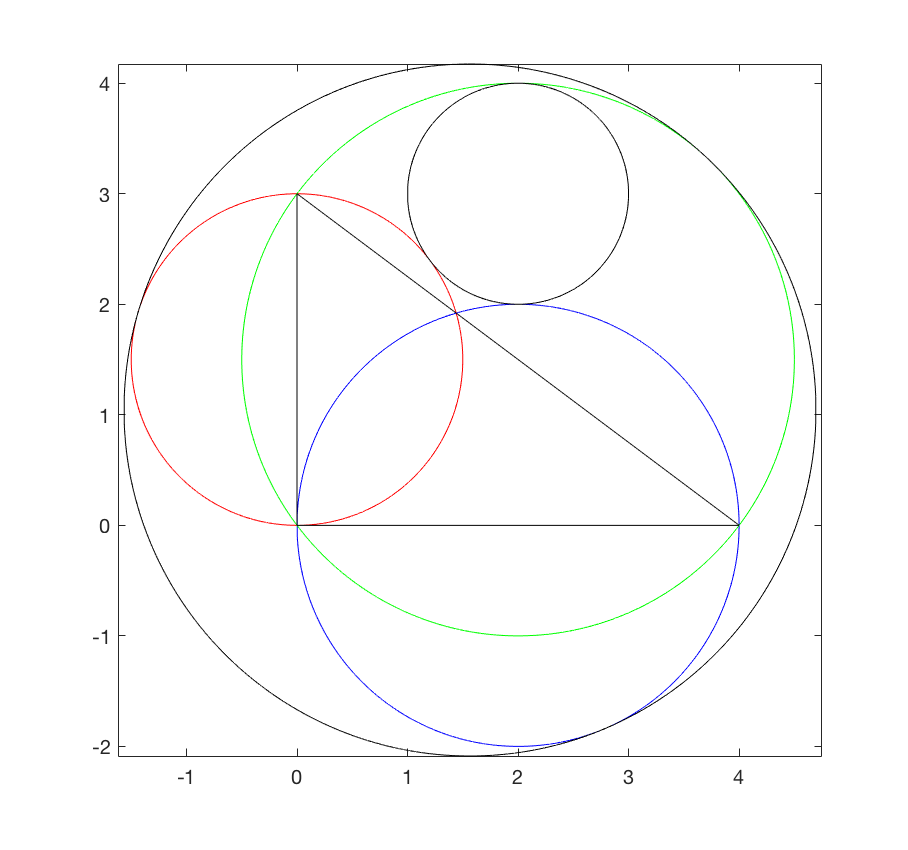
The red, blue, and green circles have diameters 3, 4, and 5, respectively.
What is the radius of the black circle tangent to all three of these circles (to 5 decimal places)?
The answer is 3.13043.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Got a proof?
Log in to reply
hold on while I get it together
okay, see proof
Log in to reply
Yup, same approach too!
Follow up question: Find the total area within any of the 3 smaller circles.
EDIT: Oh wait, that's too easy. Haha!
Log in to reply
@Pi Han Goh – Let me look at the areas of the lunes.
Log in to reply
@Michael Mendrin – Wait, isn't it just: "The sum of areas of 3 semicircles + the area of the right triangle 3-4-5?"
Log in to reply
@Pi Han Goh – I'm looking to see if there's a variation of Lunes of Hippocrates in here.. when I get to it. Yes, "obviously", the circles of diameters 3 , 4 do meet on the hypotenuse.
Log in to reply
@Michael Mendrin – Yep, I can see that you're about to make another devilishly hard geometry question. I'll be waiting patiently here.
Log in to reply
@Pi Han Goh – Can you please have a look at When a Mathematician Orders a Slice of Pie ? This problem was literally years in the making, and is now one of my favorite problems that I've devised. But few seem interested.
Edti: Oh, you did solve it. Well, this problem has baffling consequences that I still haven't satisfactorily resolved for myself. I was hoping I'd get some inputs.
Log in to reply
@Michael Mendrin – Yup, I'm still reading your question and your solution. Looks very fishy but I can't explain why. I've already reshared it.
Log in to reply
@Pi Han Goh – Thanks, I just noticed that too, that you've reposted it. Yes, it sure sounds fishy, but why? The mathematician's logic is impeccable.
Log in to reply
@Michael Mendrin – I think there's some abuse of probability theory paradox here. What abuse? I don't know exactly. I'm still thinking about it.
Log in to reply
@Pi Han Goh – Please think. I'm inviting others to jump in. But, you know, talking about "abuse of probability theory", have a look at quantum physics. That does violence to "common sense about probabilities". But it works.
@Michael Mendrin – I would like to tackle your pie problem, but I'm struggling to understand that score thing. Could you try to make it more clear to me? Thanks in advance.
Log in to reply
@Uros Stojkovic – I'll add some more notes to the bottom of that problem to try to better explain it.
Well its pretty obvious that the dotted lines go through the centers of the sides of the triangle because the dotted lines are perpendicular to the smaller circles and thus go through the centers of the smaller circles
I’m so confused about where did the 3/2 come from in the first equation
Log in to reply
( 0 , 2 3 ) is the midpoint of side of length 3 , which is the center of the circle of radius 2 3
I've added a note to help clarify this.
How do you assume that the lines from the black circle pass through the midpoints of the sides of the triangle?
Log in to reply
Given any two tangent circles, their centers and point of tangency is colinear.
I've fixed the wording of note in hopes to make this more clear.
Log in to reply
Okay, I can see that now. So if the are co linear, the black lines pass through the same center points as the other circles. Perfect! Ty sir
The radius of the little circle and the radius of the big circle are along the same line (a consequence of mutual tangency) which trivially goes through the center of the little circle. This elegant observation, plus the distance formula, leads to the equations.
Why didn’t I think of this approach??
The simplest solution possible. Much better than mine. I used the law of cosine.
Excuse me, i´m confused about the first equotation. So how do you get to this equation?
Log in to reply
Look at the dotted line going from center of large circle though the midpoint of side that has length 3 . The dotted line has length r , while the radius of the circle centered at ( 0 , 2 3 ) has radius 2 3 .
Pi 3.1416 was close enough... lucky guess.
you know why most people respect einstein and hate maths.coz he tries to simplify complicated things which makes it a little bit easier for us to understand.but you guys compete each other to complicate everything to know who is more brilliant . #Be Einstein !
Log in to reply
Just ask what should be clarified and I'll try to help.
You are bad
Let's find tangent circle by applying inversion transformation, or equivalently working in complex domain and applying reciprocal transformation w = 1 / z .
Let (0,0), or the inversion centre, be the intersection of 3 circles. Other circle intersections are ( 0 , 3 ) , ( 4 , 0 ) and 2 5 1 2 ( 3 , 4 ) .
Inversion transformation transform a circle passing through centre into a line, and other circles into circles. Thus, given three circles are transformed into lines, intersecting at 3 points; while big (still unknown) tangent circle transforms into circle tangent on those three lines. Transformed intersection coordinates are:
(
0
,
3
)
(
4
,
0
)
2
5
1
2
(
3
,
4
)
⟶
⟶
⟶
(
0
,
3
1
)
(
4
1
,
0
)
(
4
1
,
3
1
)
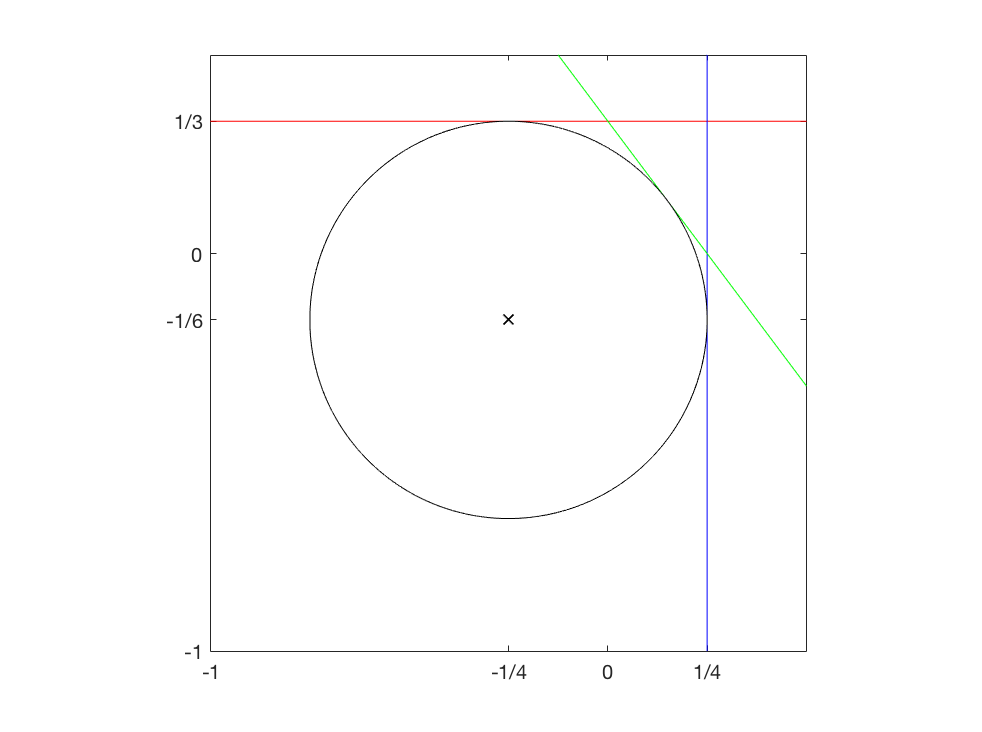
There are 4 circles that are tangent on all 3 lines: 1 inscribed and 3 escribed circle. The correct one has (0,0) in its interior. Finding coordinates of the centre and radius (solving quadratic equation) gives following circle:
c = ( − 6 1 , − 4 1 ) r = 2 1
Transforming back escribed circle gives the required tangent circle. Take notice that, while points on a circle transform into a circle, a circle centre does not transform to a corresponding circle centre. Radius of transformed circle can be deduce by working on the line that connects origin and centre of the circle. Transforming 2 points of the circle that are collinear with circle centre and the origin gives.
2 R = ∣ ∣ ∣ ∣ c ∣ − r 1 − ∣ c ∣ + r 1 ∣ ∣ ∣ R = ∣ ∣ c ∣ 2 − r 2 ∣ r R = 2 3 7 2
Here is the picture with requested tangent circle, as well as one other tangent circle corresponding to the inscribed circle of the reciprocal space.
Is it possible to use radical center/axes or homothety for this problem?
M r e d = ( 3 / 2 0 ) , r r e d = 2 3 , M b l u e = ( 2 0 ) , r b l u e = 2 , M g r e e n = ( 3 / 2 2 ) , r g r e e n = 2 5
M b l a c k = M = ( y x ) , r b l a c k = r
l e n g t h ( v ) = v x 2 + v y 2 v , u n i t v e c ( v ) = l e n g t h ( v ) v
d r e d = l e n g t h [ M r e d + u n i t v e c ( M r e d − M ) × r r e d − M ]
d b l u e = l e n g t h [ M b l u e + u n i t v e c ( M b l u e − M ) × r b l u e − M ]
d g r e e n = l e n g t h [ M g r e e n + u n i t v e c ( M g r e e n − M ) × r g r e e n − M ]
( 3 / 2 0 ) + ( 0 − x ) 2 + ( 3 / 2 − y ) 2 ( 3 / 2 0 ) − ( y x ) × 2 3 − M ⇒ d r e d = ( − x − 4 x 2 + ( 3 − 2 y ) 2 3 x ) 2 + ( 3 / 2 − y + 2 4 x 2 + ( 3 − 2 y ) 2 9 − 6 y ) 2
( 0 2 ) + ( 2 − x ) 2 + ( 0 − y ) 2 ( 0 2 ) − ( y x ) × 2 − M ⇒ d b l u e = ( 2 − x + ( − 2 + x ) 2 + y 2 4 − 2 x ) 2 + ( − y − ( − 2 + x ) 2 + y 2 2 y ) 2
( 3 / 2 2 ) + ( 2 − x ) 2 + ( 3 / 2 − y ) 2 ( 3 / 2 2 ) − ( y x ) × 2 5 − M ⇒ d r e d = ( 2 − x − 2 5 + 4 x ( − 4 + x ) + 4 y ( − 3 + y ) 5 ( − 2 + x ) ) 2 + ( 3 / 2 − y + 2 ( − 2 + x ) 2 + ( − 3 / 2 + y ) 2 5 ( 3 / 2 − y ) ) 2
Setting these 3 equations to r and solving for x,y,r of the black circle results in:
x = 2 3 3 6 , y = 2 3 2 4 , r = 2 3 7 2
It is simply the Apollonius Problem and solved by the following three quadratic equations using WolframAlpha for center (x,y) and radius 'r' of the biggest circle, which is tangent to other three circles;
(1) x^2+(y-3/2)^2=(r-3/2)^2, circle on side of length=3,
(2) (x-2)^2+y^2=(r-2)^2, circle on side of length =4,
(3) (x-2)^2+(y-3/2)^2=(r-5/2)^2. circle on side of length=5.
The solution is x=36/23, y=24/23 and radius 'r' is the Answer=72/23.
Beside that i solved the equations myself....yeah i did the same
i don´t get why (r-3/2)^2 ; (r-2)^2 and (r-5/2)^2. can you explain it to me? thank you.
Log in to reply
If you study the Apollonius problem of circles tangent to three circles as given in "https://en.m.wikipedia.org/wiki/Problem of Apollonius", you will find that to get the largest circle, which is encircling all the three circles, we need to choose negative sign in RHS of all the three quadratic equations i.e. (r-ri)^2, r1=3/2, r2=4/2 and r3=5/2.
Here, 3, 4 and 5 are the diameters of the three semi-circles on the three sides of the triangle.
I hope it clears the doubt.
Argggghhhh. Couldn't come up with the centers and tangency being colinear thought.
I did a gross guess of center and radius and looked at the distance between intersection points with the smaller circles (w/ java). And then adjusted the center and radius while using the intersection distances in each circle as a guide to subsequent guesses until the accuracy was beyond 5 places. A decent mastery of geometry would have saved a lot of work.
not really well. Explained. ould do better if tried harder. Just as. 3+2 = 6-1
That should doit.
LC


Radius is exactly 2 3 7 2 , pretty neat. See the figure below, where dotted lines from the center of the circumcribing circle passes through the midpoints of the sides of the triangle.
Let B be the origin ( 0 , 0 ) , and the center of circle of unknown radius r be ( x , y ) . Then we solve the following three equations to find r
2 3 + x 2 + ( 2 3 − y ) 2 = r
2 + ( 2 − x ) 2 + y 2 = r
2 5 + ( 2 − x ) 2 + ( 2 3 − y ) 2 = r
so that ( r , x , y ) = ( 2 3 7 2 , 2 3 3 6 , 2 3 2 4 )
Note: The midpoints of the sides ( 0 , 2 3 ) , ( 2 , 0 ) , and ( 2 , 2 3 ) are centers of circles of radii 2 3 , 2 , 2 5 .
Given any two tangent circles, their centers and point of tangency is colinear.
Bonus: If right triangle A B C has rational sides, then ( r , x , y ) are also all rationals.