Circle in Semicircle
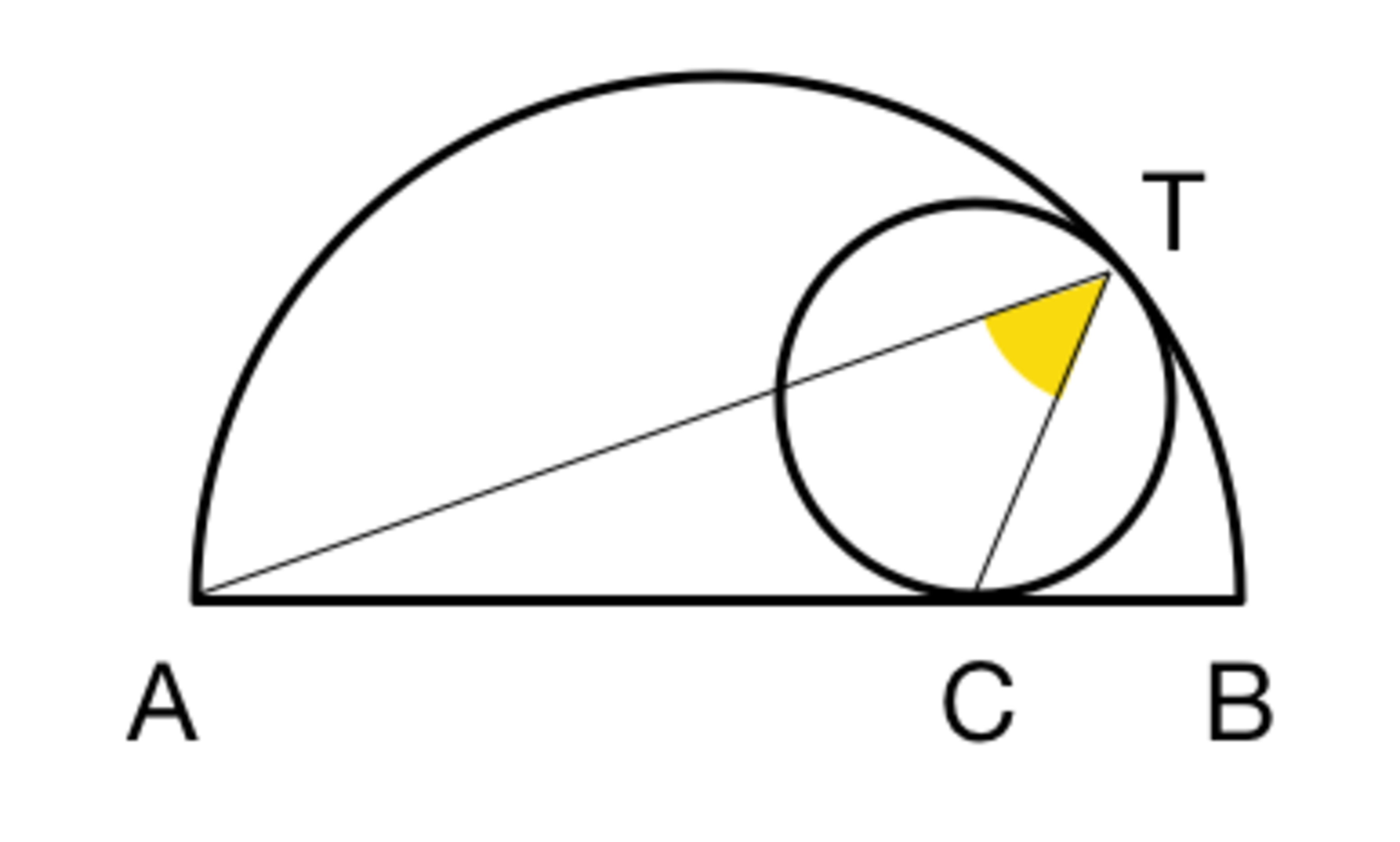
AB is the diameter of the semicircle.
A circle is tangential to the diameter at C, and the circumference at T.
What is the angle ∠ A T C ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Okay, I think you need to mention that the vertical line is always tangent to the small circle and perpendicular to the horizontal one.
Log in to reply
"You" meaning me or Calvin? Calvin has stated only what needs to be stated. But I'll be revising my previously posted solution.
Log in to reply
'You' meaning you. I mean when I first looked at your solution I thought that the vertical line was meant to be the diameter.
Log in to reply
@Wen Z – I just posted a revised solution, so that we can get rid of any talk about the vertical diameter being tangent to the circle. Thanks for pointing out my oversight.
Let A T intersect the smaller circle at D . ∠ A T C = ∠ A C D = x (Alternate Segment Theorem).
We have ∠ A T B = 9 0 ∘ (Angle subtended at Circumference by the diameter) so ∠ C T B = 9 0 − x .
Draw the common tangent go both circles at T .Call it P Q with P closer to B . Let ∠ B T P = y .
We have ∠ C T P = ∠ C T B + ∠ B T P = ∠ C D T = 9 0 + y − x and ∠ B T P = ∠ B A T = y (Alternate Segment Theorem).
Considering Δ D C T we get ∠ D C T = 9 0 − y . Hence, ∠ T C A = ∠ A C D + ∠ D C T = x + 9 0 − y .
In Δ A T C , we have y + ( x + 9 0 − y ) + x = 1 8 0 or 9 0 + 2 x = 1 8 0 or x = 4 5 ∘ .
Hence, ∠ A T C = x = 4 5 ∘ .
It was slightly hard to follow what you were doing. There were times that you skipped steps in the angle chasing, like explaining why ∠ T C A = ( x + 9 0 − y ) .
Log in to reply
I had a typo in the third last line. I have added the step of finding angle TCA too.
Log in to reply
Thanks for improving it! I now understand what you're doing.
You should justify why "TCD is a straight line". That is the crucial step needed, which uses euclidean geometry - homothety in Michael's solution.
Log in to reply

Log in to reply
That's a possible approach.
For completeness, note that you are assuming that TIO is a straight line, which follows from the perpendicular to the tangent passes through the center of the circle.
Log in to reply
@Calvin Lin – since point "T" is common tangent point of two circles , then the common tangent line at "T" must be perpendicular onto the radius of each circle. i.e OT and IT are perpendicular onto common tangent line at "T'.
Therefore, O,I and T are collinear. ---> TIO is a straight line
Jon, I think Calvin wants to promote a Homethety program, which is an interesting way to solve geometrical problems more efficiently.
Log in to reply
Ah yes. Thanks for pointing it out. I believe we've featured the other problem, so I will not feature this problem.
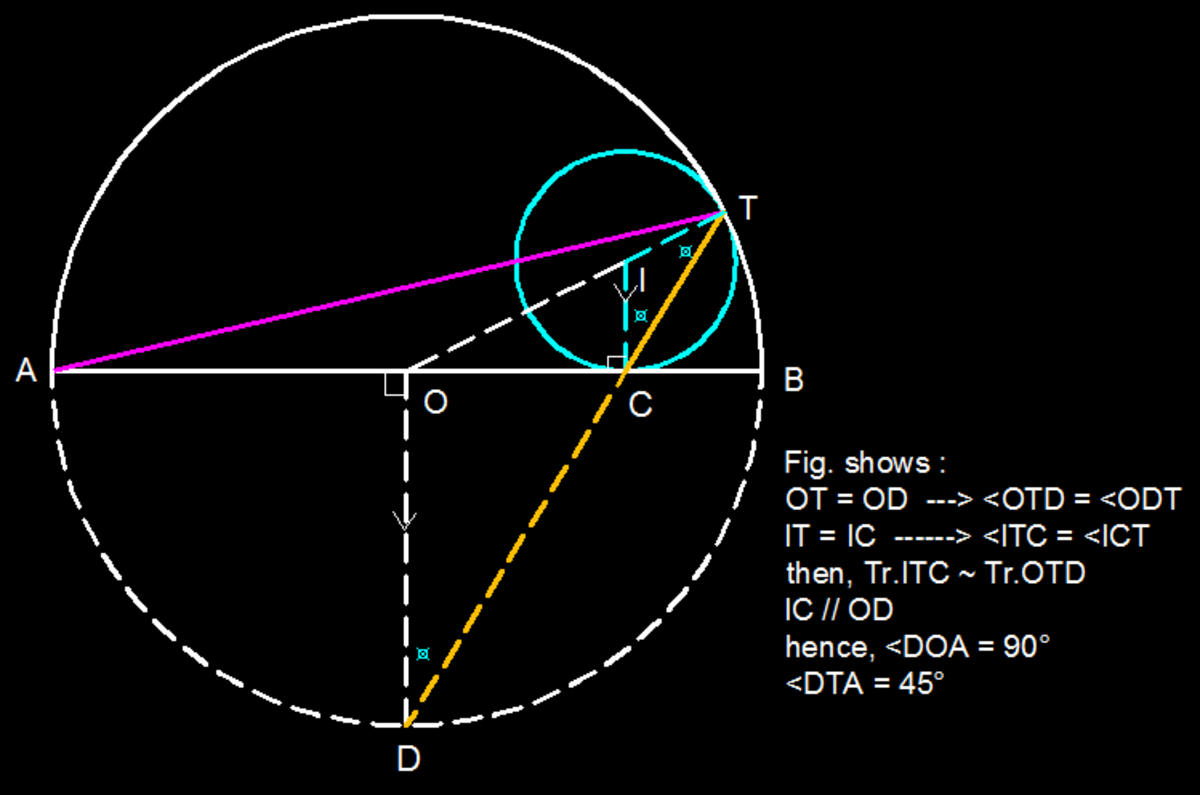
Consider a homethety with center O where small and large circles are in tangent. Diameter d is then parallel with line e , so that point A ′ in passing through center C of large circle is another diameter f that is perpendicular to d . ∠ B ′ C A ′ = 9 0 ° , and so therefore ∠ B ′ O A ′ = 4 5 ° .