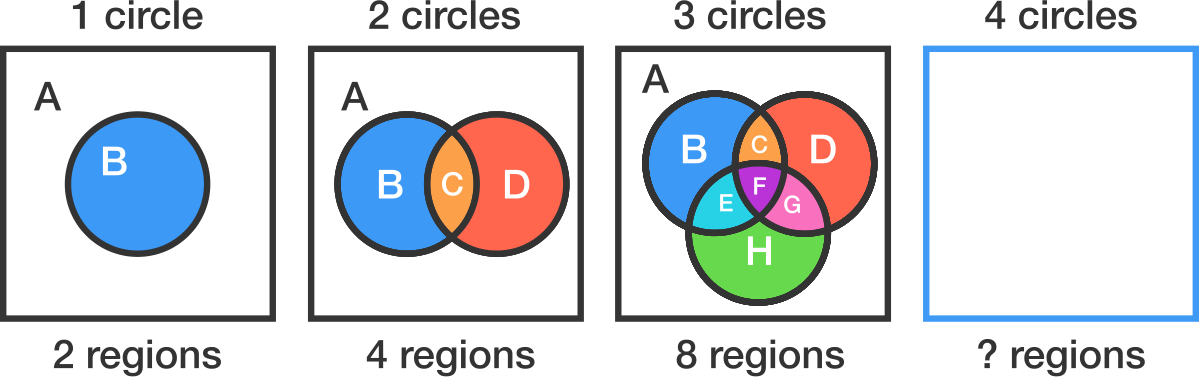
Circles
1 circle can split the plane into at most 2 regions.
2 circles can split the plane into at most 4 regions.
3 circles can split the plane into at most 8 regions.
4 circles can split the plane into at most ______ regions.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
How do we show that a circle intersecting all existing k − 1 circles at 2 ( k − 1 ) distinct points exists?
Log in to reply
You're just wanting a constructive way of fulfilling the number of intersections; one way is to just put all the circles in a line and have them be of increasing radius, so that the rightmost circle just makes it inside the leftmost circle.
An interesting consequence is that we cannot explain all situations of a family of 4 sets with Venn Diagrams.
This is the best explanation hands down. Thanks.
4 circles can split the plane into at most 1 4 regions
How do you know that 15 (or higher) cannot be achieved?
Log in to reply
There are lots of problems that are related to the sources outside, much like this one that relates to WM article .
This problem can be solved by proving that the number of divided regions is n 2 − n + 2 , or observing the number of regions.
Log in to reply
This problem can be solved by proving a harder problem that generalizes this problem. Well, OK then. So how would that be done? Edit: I see the page linked to doesn't answer that question, either. Anybody got a reference to the source of the proof of this formula?
Log in to reply
@Richard Desper – Each circle can only intersect any other circle at at most 2 points, thus a new circle in a plane in which 3 are already present can have at most 6 new intersections. which creates at most 6 new areas. 8 + 6 = 14
Also can solve by 2^n-n
Relevant wiki: Arithmetic Progression Sum
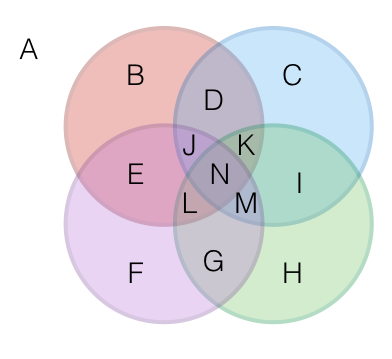
Assume this follows alphabetical orders. Look at the first 3 pictures,
Circle 1: 2 regions → A , B
Circle 2: 4 regions → A , B , 2 C , D
Circle 3: 8 regions → A , B , C , D , 4 E , F , G , H
So for circle 4 it will be 1 4 regions → A , B , C , D , E , F , G , H , 6 I , J , K , L , M , N
So following this pattern, circle 5 will be 22 regions? 14+8
Log in to reply
Yes, for circle 5 it will be 22 regions.
Log in to reply
i think circle 5 will 'have' or 5 circles will have.
Well, this does not say anything. Why should this pattern be followed?
the number of split regions will be= n 2 − n + 2
so,for 4 circles the region numbers will be = 4 2 − 4 + 2 = 1 4
explanation:this can be solved in 3 ways....
number-1....look at the difference of this pattern------2............4.............8............14.....
................................................... difference------------------2-----------4------------6-----------........................[everytime the difference before+2]
number-2.....[2,4,8,14].....this pattern can be generalized as (a) 2 n − 2 .....() or n 2 − n + 2 .......[this will also give the same result]
number-3.....look at this set region.......1 circle=1 region,.....2 circles=3 regions,....... 3 circles=7 regions...[not adding the outer part ]
...................so, from that pattern it is easy to say that if 4 circles there will be =13 regions.and total regions in 4 circles will
be= 1 3 + 1 = 1 4 ...........[adding the U set or outer set]
You need to be able to prove that generalization. Where did n 2 − n + 2 come from?
Log in to reply
oh! that is a pretty simple and easy pattern to guess.this can be solved in many ways.......
number-1....look at the difference of this pattern------2............4.............8............14.....
................................................... difference------------------2-----------4------------6-----------........................[everytime the difference before+2]
number-2.....[2,4,8,14].....this pattern can be generalized as (a).....( 2 n − 2 ) or ( n 2 − n + 2 ).......[this will also give the same result]
number-3.....look at this set region.......1 circle=1 region,.....2 circles=3 regions,....... 3 circles=7 regions...[not adding the outer part ]
...................so, from that pattern it is easy to say that if 4 circles there will be =13 regions.and total regions in 4 circles will
be= 1 3 + 1 = 1 4 ...........[adding the U set or outer set]
Log in to reply
Why n = 4 ?
Log in to reply
@Munem Shahriar – only 1 circle---n=1,......................this is going like that. if you look at the pattern you will lough how funny question this is.
Log in to reply
@Mohammad Khaza – I do not understand.
Log in to reply
@Munem Shahriar – just look at number-1 (pattern)-----2...4...8.....14....you can generalize the pattern with .... n 2 − n + 2 or 2 n − 1 .
everything in this world has an abstract pattern which can be generalized by mathematics.for this picture of circles the pattern---2...4...8....14.
so, for 1st sequence,n=1 ; for 2nd sequence,n=2...............
Doesn't work for n = 0. Where if n = 0, there would be 1 region.
a(2) - a(1) = 2, a(3) - a(2) = 4, ... a(n)-a(n-1) = 2(n - 1) (n-1 circles will split a circle into at most n-1 regions)
so:
a(n) - a(1) = 2+4+...+2(n - 1) = 2(1+2+...+n-1) = n^2 - n
a(n) = n^2 - n + 2 (n>=1)
We can solve this problem by first solving it for lines (instead of circles) and then using stereographic projection to extend it to circles:
Whenever in a plane we have parallel lines or more than 2 lines intersect at the same point, we can add new regions (without destroying any existing ones) by slightly perturbing the lines involved. So for maximizing the number of regions we assume that no 2 lines are parallel and no 3 of them meet at a point. Given n such lines in plane P , each pair of them will intersect exactly once, at a point unique to the pair, for a total of
V = n C 2
points of intersection, and each line will be partitioned into n − 2 bounded and 2 unbounded segments by its n − 1 points of intersection with the other lines. That's a total of
E = n ⋅ ( n − 2 )
bounded and 2 n unbounded segments. Since each unbounded region borders on 2 unbounded segments and each unbounded segment iborders on 2 unbounded regions, there are
U = 2 n
unbounded regions. To find the number B of bounded regions, let's temporarily remove all the unbounded segments leaving behind a finite planar graph with a total of F = B + 1 regions (including the 1 unbounded one). Using Euler's V − E + F = 2 we can find that
B = F − 1
= ( E − V + 2 ) − 1
= E − V + 1 .
This solved the problem for n lines. Now stereographically project P ∪ { ∞ } to a sphere S . Then S will be partitioned by n circles into B + U regions with all n circles intersecting at the north pole. We can perturb these n circles away from the north pole without destroying any of the U regions already there locally resulting in B + U regions, just like we did with the lines. Globally this will have added B new regions to the B + U already present, for a total of 2 B + U regions. Projecting S back onto P results in n circles, partitioning P into
2 B + U
= 2 ( E − V + 1 ) + 2 n
= 2 ( n ⋅ ( n − 2 ) − n C 2 + 1 ) + 2 n
= n 2 − n + 2
regions.
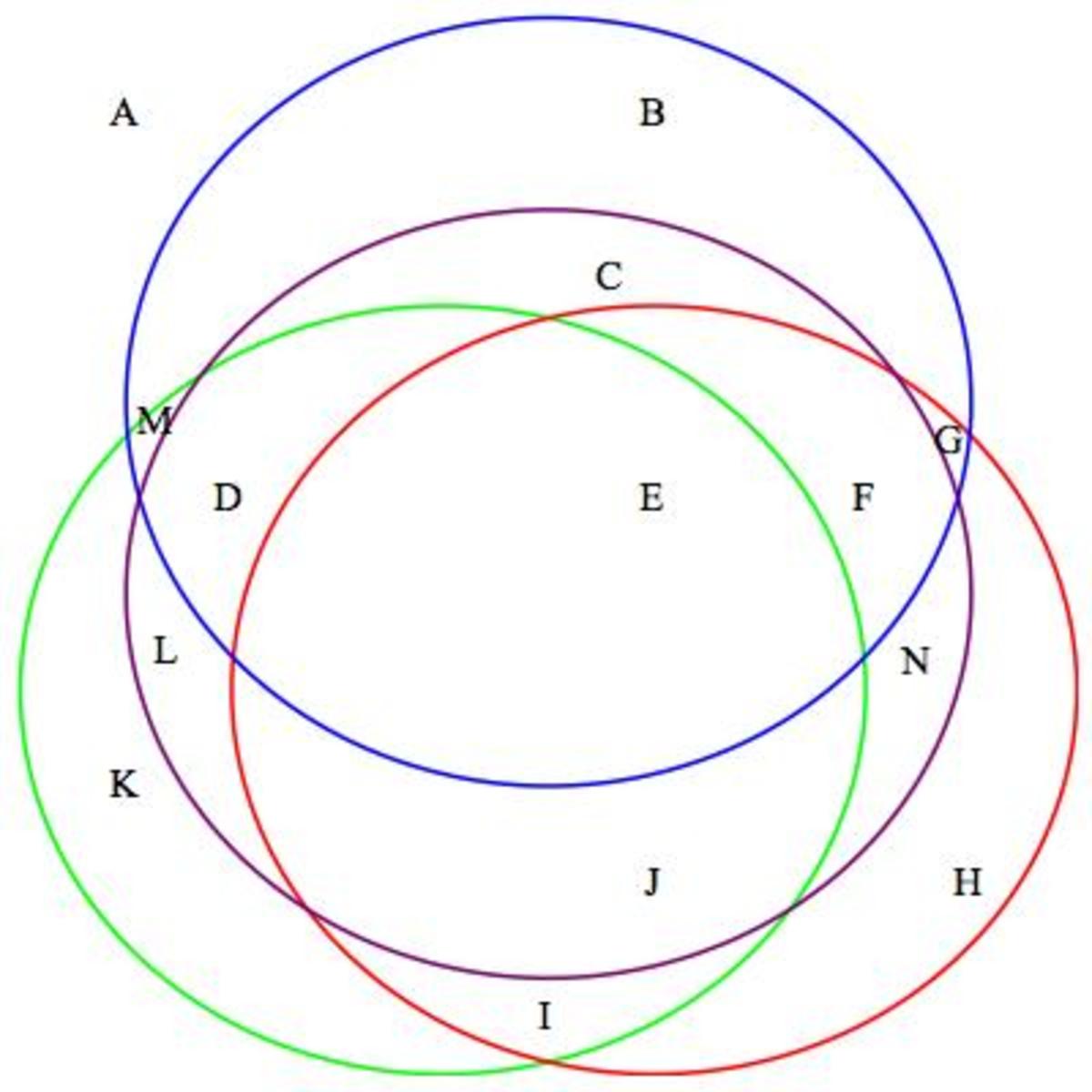
So, there are 14 regions A thru N.
Imagine the pattern in the number of regions without A since regions are the being added to the circles only.
Number of total regions - A:
1 circle: 1 regions
2 circles: 3 regions
(2 added to the 1st region)
3 circles: 7 regions
(4 added to the previous 4 regions)
If you notice the pattern you can see that to find the # of regions for 4 circles we need to add 6 to the previous 7 regions.
4 circles: 7 + 6 = 13 regions
Since we just calculated the # of regions without A we must add that back in for the total #.
Therefore, 4 circles can split the plane into at most 13 +1 = 14 total regions
No proof yet that 14 is correct. Just pictures with counting or guesses that 0,2,4 implies that the next number is 6, the other solution like it.
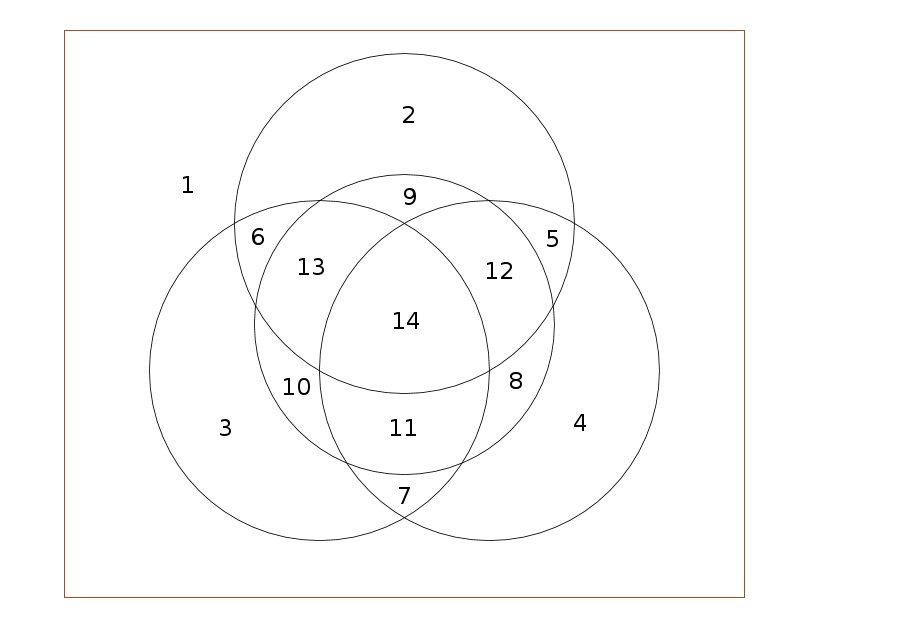
First note we can't do any better: a set of circles will divide the plane into a maximal number of areas if every possible pair intersects and no three are concurrent.
If we look at adding the k th circle to an existing arrangement, it intersects each of the existing k − 1 circles in 2 points, resulting in 2 ( k − 1 ) intersections and dividing the new k th circle into 2 ( k − 1 ) arcs. Each arc splits one of the existing regions into two, as shown below.
Now let's justify the general formula (mentioned but not proven in other solutions) using this. As noted here, the 3rd circle increases the count by 2 ( 3 − 1 ) = 2 ( 2 ) = 4 , the 4th circle increases the count by 2 ( 4 − 1 ) = 2 × 3 = 6 , the 5th circle increases the count by 2 ( 5 − 1 ) = 2 ( 4 ) = 8 , and so on. (The first circle is unique in that it makes 2 regions even though it has no intersections.)
For n circles, this results in the summation
2 + 2 + 4 + 6 + 8 + … + 2 ( n − 1 ) = 2 + 2 ( 1 + 2 + 3 + 4 + … + ( n − 1 ) )
After applying the arithmetic sum formula, this simplifies to
2 + 2 2 n ( n − 1 ) = n 2 − n + 2