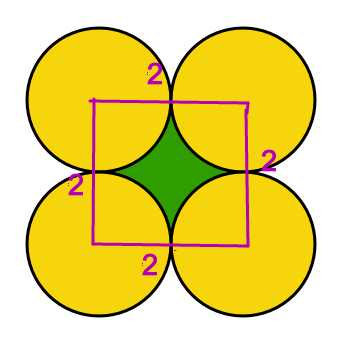
Circles Abound
Within the orange square, there are 4 circles each with radius 1. What is the area of the green region in the center?
Hint: Connect the centers of the circles.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
Nice solution! Diagram says it all
What application do you use to make the picture?
Log in to reply
Copy the image from the problem and then edit it in Paint.exe.
Log in to reply
Oohh.. I am still finding a good application to make a diagram.. Hehehe
Log in to reply
@Fidel Simanjuntak – @Chung Kevin what application did you use to make the diagram?
Log in to reply
@Fidel Simanjuntak – I create my images using OmniGraffle on a Mac.
Brilliant will improve on the images for problems that are popular, so it doesn't really matter what application you use. They use Figma to create vector images, but I rather use something I'm comfortable with. Others have created images using Paint, or even Microsoft word.
Why would it be a square? I mean, why would all angles be 90 degree?
Log in to reply
You are right. I have made an assumption.
Log in to reply
That's right! Thanks for pointing out that there isn't enough information to solve this problem completely (other than eyeballing the image).
I've now added a condition to ensure that the configuration is a square. Previously, the image had a unwritten assumption about the arrangement of the circles and their tangencies.
We get a square of side 2 units by joining all the centres of the circle.
The square has yellow part & green part.
The yellow part consists of 4 congruent quadrants of a circle. (They are congruent because they all have central angle 90 and radius 1)
Hence, the area of yellow part = Area of circle with radius 1 = π * 1 * 1 = π
Area of the square = side * side = 4
Therefore, Green region = Area of square - Area of yellow region = 4 - π
Why would it be a square? I mean, why would all angles be 90 degree?
you did it the same as me. im a math prodidgy. i totaly agree with you
If we join the centres of all circles , we will get a square with side = 2×radius of circle = 2 | Area of square = Area of four quadrants + Green Area | Since all circles are congruent , the four quadrants will make up a complete circle with radius = 1 | 2×2 = π×1×1 + Green Area | Therefore , Green Area = 4-π . ||
That's nice. Gives us the green region directly.
What I did is different
I put a square aroud it all, so the side of the square would be 2 * D = 4 * R = 4
So the square area is 4*4
now, the area of each circle is π, so I remove it from the square -> A = 4*4 - 4π = 4 ( 4 - π)
Now, the blank spaces and the green spaces sum up to 4(4-π)
The blank spaces on the sides sum up to to green area, also, the area of the top and bottom sum up to the same green area, while the corners sum up to the green area, so we have A = 4 *G
So 4G = 4(4-π) => G = 4-π
Log in to reply
Yes, this is an interesting approach.
From this image we will only focus on what is inside the 2x2 square. We can see that the areas of the 4 quarter circles are each 1/4 π, so the total of those areas is π. The area of the square is 4, so the area of the green region is 4-π .
This is a nice way to look at the figure! We can picture the green area as four quarter circles removed from a square.
Focusing on one quadrant: Green Area = 4 Square of sidelength 2 − circle of radius 1
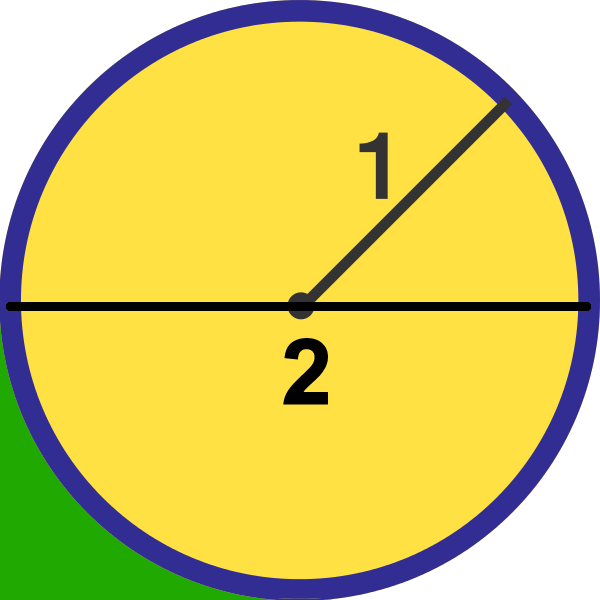
If we consider the entire diagram, the total green area is 4 times this amount, and is therefore a Square of sidelength 2 − circle of radius 1 = 2 2 − π = 4 − π .
This is probably the neatest solution I've seen here~~! Nicee
Relevant wiki: Length and Area Problem Solving
 Clearly from the diagram,
Clearly from the diagram,
Area of Green Region=Area of Red Square - Area of the Circle Inside the Red Square= 2 2 − ( π × 1 × 1 ) = 4 − π
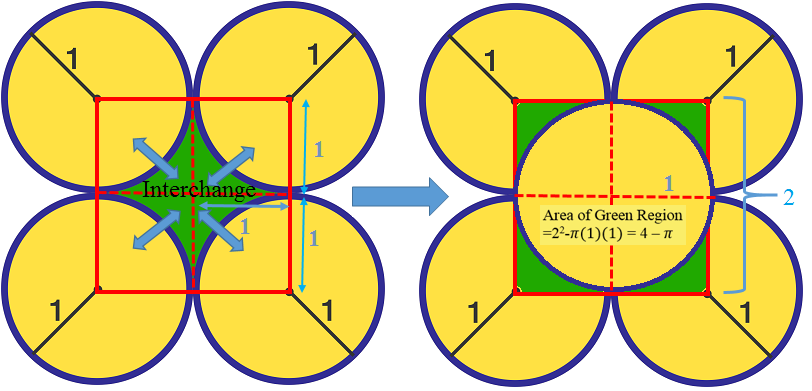
oh! I didn't thought about rearranging the green regions. The picture on the right makes it so much easier to solve the question. Thanks!
Log in to reply
Thank you for the comments. Visualization & little imagination will give the solution in the fewest steps.
As each circle has radius 1, area of all the 4 circles= π r 2 ∗ 4 = 4 π . If we make a square on the boundary of the figure, we can notice that 1 more the same shape as the green region can be contained in the square. Thus, area of green region= 2 1 6 − 4 π , which can be reduced to 4 − π . That is the answer!
Actually, it is "total of 4 green regions in the square".
Your division is off. Instead, it should be 4 1 6 − 4 π = 4 − π .
Ok! Thanks for pointing out. I will check if I write a solution next time.
The 'white' area inside the square is 2 times the 'green' area.
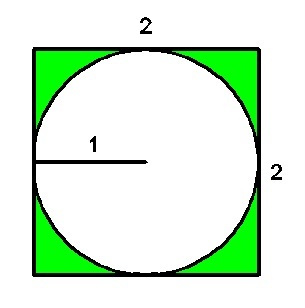
Area of green region = area of square - area of circle = 2 2 − π ( 1 2 ) = 4 − π
Good image. It makes your solution clear and easy to understand.
Make a square of 4 by 4 units around the four circles, let the required green area be =x
So now, area of square - area of circle=4x
As we can see from symmetricity that the part between any two circle and the edge of the square has an area x/2 and there are 4 such parts so these parts have area 2x and the part between a circle and the corner of the square has an area x/4 and there are 4 such parts so they give an area x,
Now, area of square - area of circle = 16-4π
=x(green part) + 2x +x = 4x
So, x= (16-4π)/4= 4-π
Which is the required area.
Oh this is an interesting way to look at the figure. There will be a total of four times the green area in the big square.
The green area is equivalent to the bits of area between the unit circle and the square subscribing it.
Easy.
Area of each circle = 1*∏ = ∏
Circumscribe one of the circles with a square with side = 2
Area of the square = 2*2=4
Area of that part of the square outside the circle = 4-∏
Area of the green area inside the square = (4-∏)/4
True for all four circles
Therefore the combined green area = 4*(4-∏)/4 = 4-∏
I assume the weirdly rendered character is pi. Your solution is very easy to follow!
There is four circle having same radius so we can have area of square by joining there circle is=4,and every circle contribute his 1/4th part so area of one circle is=3.14/4 (2)^2,and area covered by four circle in square is 4 (area of one circle covered) is directly=3.14 so we can write the soution as=4-3.14.hence solved.
Yes, that is a valid approach.
From the figure above, it is clear that the area of the green region is the area of the 2 × 2 square minus the area of 4 quadrants of radius 1 or a circle of radius 1, or A = 2 × 2 − π × 1 2 = 4 − π .