circles and squares make dizzy!
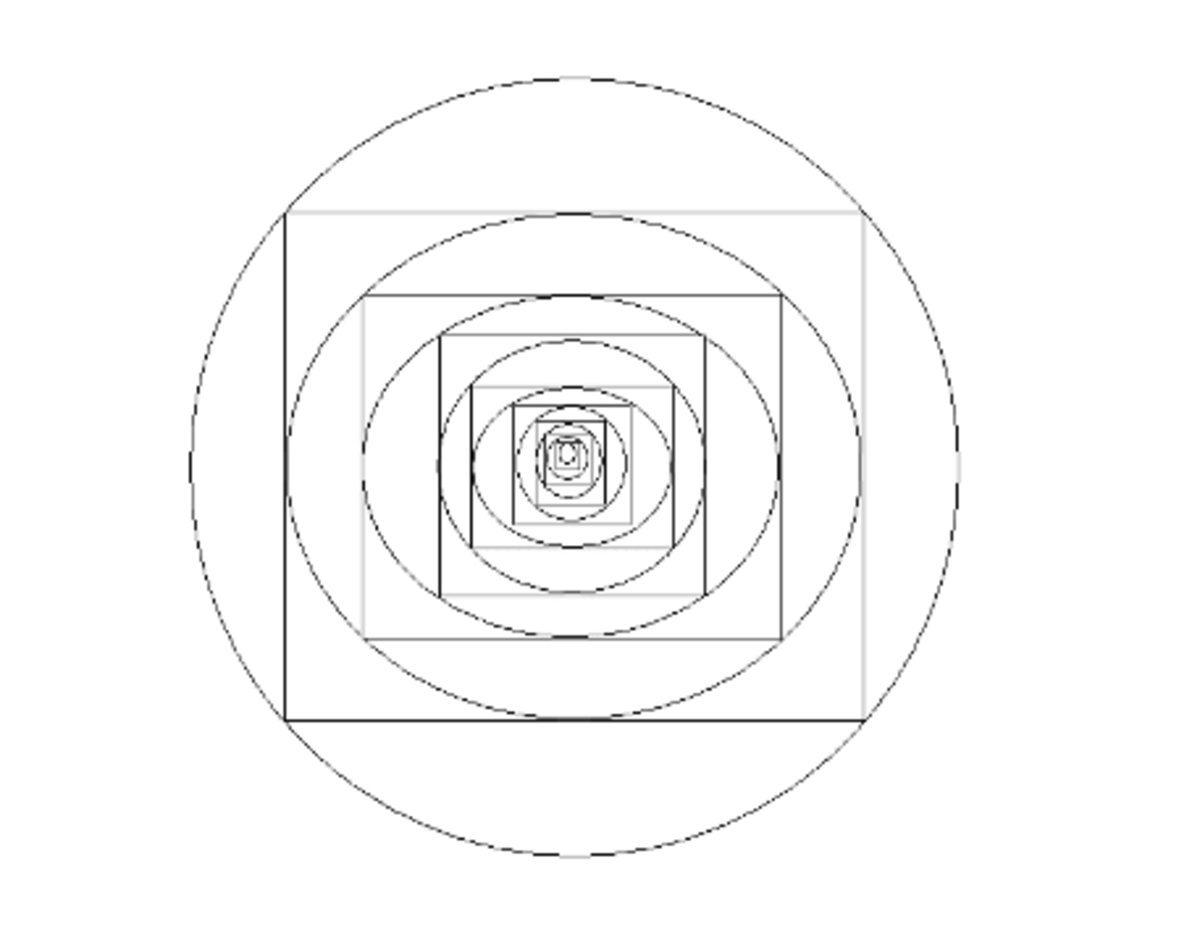
Starting from a circle of radius r, squares and circles are inscribed one inside the other and the process goes on.
If the total area of the circles and squares can be expressed as
A
π
r
2
+
B
r
2
, where
A
and
B
are rational numbers. Find
A
+
B
.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you sir, I have replied to him on his solution. And, good solution! +1.
area is given as:
circle: { \Pi r }^{ 2\quad } .......................................where r is radius
square: \frac { { (d) }^{ 2 } }{ 2 } ............................. where d is diagonal
so total area is:
{ \Pi r }^{ 2\quad }+\frac { { (2r) }^{ 2 } }{ 2 } \quad \quad +\quad \quad \quad { \Pi (\sfrac { r }{ \sqrt { 2 } } ) }^{ 2\quad }+\quad \frac { { (\sfrac { 2r }{ \sqrt { 2 } } ) }^{ 2 } }{ 2 } \quad \quad +\quad \quad \quad { \Pi (\sfrac { r }{ \sqrt { 2 } \sqrt { 2 } } ) }^{ 2\quad }+\quad \frac { { (\sfrac { 2r }{ \sqrt { 2 } \sqrt { 2 } } ) }^{ 2 } }{ 2 } and so on...........
using G.P. we get: { 2\Pi r }^{ 2\quad }+4{ r }^{ 2 }
hence a+b=6
Hi Mihir.
Good work on the solution! You might like to improve your LaTeX. I see that you know the codes, just ensure that they are wrapped in \ ( ...\ ) [Without spaces] for proper rendering. Thanks!
a
r
e
a
i
s
g
i
v
e
n
a
s
:
c
i
r
c
l
e
:
π
∗
r
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
w
h
e
r
e
r
i
s
r
a
d
i
u
s
s
q
u
a
r
e
:
2
d
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
w
h
e
r
e
d
i
s
d
i
a
g
o
n
a
l
s
o
t
o
t
a
l
a
r
e
a
i
s
:
{
π
∗
r
2
+
2
(
2
r
)
2
}
+
{
π
∗
(
2
r
)
2
+
2
(
2
2
r
)
2
}
+
{
π
∗
(
2
∗
2
r
)
2
+
2
(
2
∗
2
2
r
)
2
}
a
n
d
s
o
o
n
.
.
.
.
.
.
.
.
.
.
.
u
s
i
n
g
G
.
P
.
w
e
g
e
t
:
{
2
π
∗
r
2
}
+
4
{
r
2
}
h
e
n
c
e
a
+
b
=
6
I have tried to see that your Latex work.
Log in to reply
@Niranjan Khanderia Sir, please refrain from using text in LaTeX. Your solution is great, but the LaTeX-ed text makes is look more stuffy. Thanks!
Log in to reply
I was trying to put Mihir Parikh's codes in LaTex. Please see my solution. Do comment what I should do to improve. I will welcome your comment.
Log in to reply
@Niranjan Khanderia – Your solution is perfect. Sorry for the inconvenience! :)
A r e a s a r e : − c i r c l e : π r 2 . . . . . . . . . . . . . . where r is radius
s q u a r e : 2 d 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . where d is diagonal= 2r.
so total area is:
{ π ∗ r 2 + 2 ( 2 r ) 2 } + { π ∗ 2 r 2 + 4 ( 2 r ) 2 } + { π ∗ 4 r 2 + 8 ( 2 r ) 2 } . . . . . . . . = π ∗ r 2 { 1 + 2 1 + 4 1 + 8 1 . . . . . . } + 2 ∗ r 2 { 1 + 2 1 + 4 1 + 8 1 } . . . . . . . . . . . = π ∗ r 2 ∗ 1 − 2 1 1 + 2 ∗ r 2 ∗ 1 − 2 1 1 = 2 ∗ π ∗ r 2 + 2 ∗ 2 r 2 = A ∗ π ∗ r 2 + B ∗ r 2 ∴ A + B = 6
It is the same as Mihir Parikh.
Since your Reply is not working, comment for you( Mihir Parikh) . You should enclose your Latex in\ (........\ ),NO space afterboth \ here. I have to keep that to show you..
For\Pi it should be \pi , it is not \sfrac but \dfrac , If you have only single exponent no need of {..}, just X^2, also \sqrt2. \quad not required in maths.