Circles and triangles
The red, blue, and green circles in the figure below have diameters 3, 4, and 5, respectively.
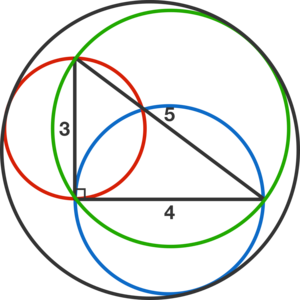
What is the radius of the black circle tangent to all three of these circles?
If this radius can be expressed as b a , where a and b are coprime positive integers, submit your answer as a + b .
The answer is 95.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Can this sum be done by Euclidean Geometry only? If so please send the solution, I'm curious.
How do you know it’s the midpoint? Thanks.
Log in to reply
The midpoint of any diameter is also the center of the circle.
Log in to reply
Thanks for your response! What I don’t understand is how you know that OG, OI, and OH cut through points D, F and E respectively. Hope it makes sense.
Log in to reply
@Aradhya Kasera – Since the red circle is tangent to the black circle at G, the radius of the black circle must pass through the center of the red circle, so G, D, and O are collinear. A similar argument can be made for H, E, and O and I, F, and O.
Log in to reply
@David Vreken – Sorry to keep pestering you but I still don’t get it! Is it some kind of standard result? A circle inscribed of another circle - the radius of the outer circle passes through the centre? Thanks again! Truly appreciate your help.
Log in to reply
@Aradhya Kasera – If you draw a tangent line m at G, the radius of the black circle is perpendicular to m at G, and the radius of the red circle is perpendicular to m at G, so G, D, and O must be collinear.
Also see this website which says "A special property can be noted when the two circles are tangent to each other: As this common tangent line is perpendicular to both radii of each circle at that point, it follows that the two radii and the tangent point lie along the same line."
can you do planets plss 😇😇😇😇
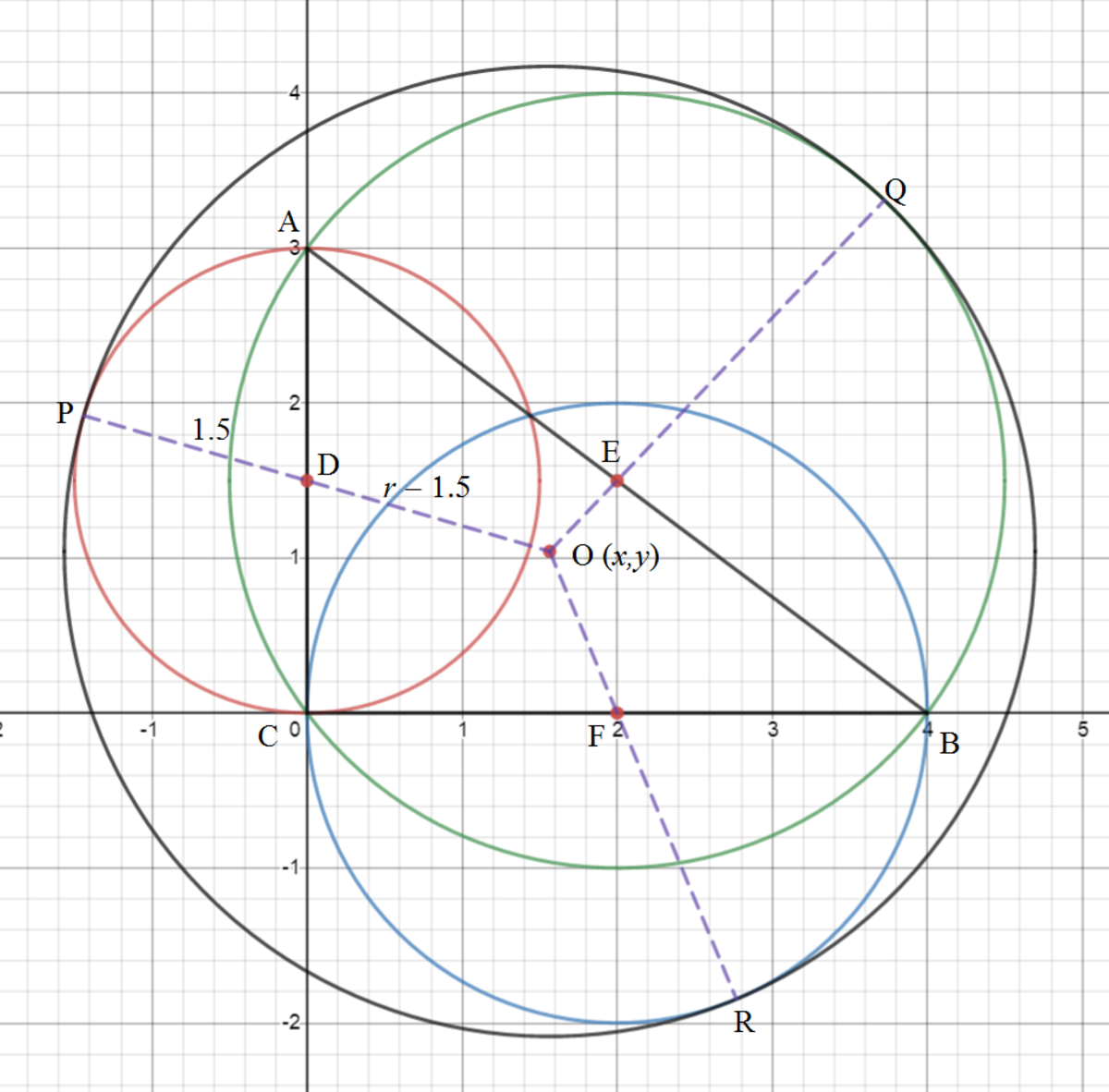
Let the vertices of the triangle be A ( 0 , 3 ) , B ( 4 , 0 ) , and C ( 0 , 0 ) . The midpoints of the triangle sides are D ( 0 , 1 . 5 ) , E ( 2 , 1 . 5 ) , and F ( 2 , 0 ) . Let the center of the black circle be O ( x , y ) and its radius be r , and the tangent points of circles be P , Q , and R as shown.
We note that P , D , and O are colinear and that O P = r and D P = 1 . 5 , hence O D = r − 1 . 5 . Using the coordinates of D ( 0 , 1 . 5 ) and O ( x , y ) and Pythagorean theorem , we have x 2 + ( y − 1 . 5 ) 2 = ( r − 1 . 5 ) 2 . Similarly for O R and O Q , and we get the following three equations.
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ x 2 + ( y − 2 3 ) 2 ( x − 2 ) 2 + y 2 ( x − 2 ) 2 + ( y − 2 3 ) 2 = ( r − 2 3 ) 2 = ( r − 2 ) 2 = ( r − 2 5 ) 2 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
From ( 1 ) − ( 3 ) :
x 2 − ( x − 2 ) 2 4 x − 4 ⟹ x = ( r − 2 3 ) 2 − ( r − 2 5 ) 2 = 2 r − 4 = 2 r
From ( 2 ) − ( 3 ) :
y 2 − ( y − 2 3 ) 2 3 y − 4 9 ⟹ y = ( r − 2 ) 2 − ( r − 2 5 ) 2 = r − 4 9 = 3 r
From ( 1 ) + ( 2 ) − ( 3 ) :
x 2 + y 2 4 r 2 + 9 r 2 4 r + 9 r ( 1 − 4 1 − 9 1 ) r ⟹ r = r 2 − 2 r = r ( r − 2 ) = r − 2 = 2 = 2 3 7 2
Therefore a + b = 7 2 + 2 3 = 9 5 .
How do we know that P , D , and O are collinear if we haven't fixed the location of O yet?
Did you mean to type P D = 2 3 instead of P D = 3 ?
Can you rephrase the sentence which begins with "Since D ( 0 , 1 . 5 ) ...", please? There seems to be something missing. Or maybe it's just me.
Log in to reply
Because the tangent at P is perpendicular to D P and also perpendicular to O P and there is only one straight line perpendicular to the tangent at P .
I have amended the line "Since D ( 0 , 1 . 5 ) ...". Yes it was odd,
Log in to reply
Aha. Thanks! Do you know, by chance, if the circle's center, O , is a known triangle center? i.e., is it in Kimberling's encyclopedia of triangle centers? Seems like it should be.
Can this sum be done by Euclidean Geometry only? If so please send the solution, I'm curious.

We put the triangle on a coordinate plane, so that the vertices are A ( 0 , 0 ) , B ( 0 , 3 ) and C ( 4 , 0 ) . Then, the midpoints of B C , C A and A B are D ( 2 , 1 . 5 ) , E ( 2 , 0 ) and F ( 0 , 1 . 5 ) respectively (see figure). Denote the center of the black circle and its contact points with the red, blue and green circle by K , H , I and J respectively.
Since the black and the red circles have a common tangent line at H , both H F and H K are perpendicular to this line. Hence, H , F and K are collinear. Likewise, J , D and K are collinear, as well as I , E and K . Let the radius of the black circle be R .
Then,
K F − K D = ( K H − F H ) − ( K J − D J ) = ( R − 1 . 5 ) − ( R − 2 . 5 ) = 1 This means that K lies on a hyperbola, who’s foci are F , D and with constant difference of distances 1 . In fact, K lies on the branch that is closer to focus D .
Any arbitrary point M ( x , y ) on this branch satisfies the equation
M F − M D = 1 ⇔ ( x − 0 ) 2 + ( y − 1 . 5 ) 2 − ( x − 2 ) 2 + ( y − 1 . 5 ) 2 = 1 ⇔ 3 x 2 − y 2 − 6 x + 3 y = 0 , x > 1 ( 1 ) Similarly, K E − K D = ( K I − E I ) − ( K J − D J ) = ( R − 2 ) − ( R − 2 . 5 ) = 0 . 5 .
Hence, K lies on a hyperbola, who’s foci are E , D and with constant difference of distances 0 . 5 . Again, K lies on the branch that is closer to focus D .
The equation of this branch is
( x − 2 ) 2 + ( y − 0 ) 2 − ( x − 2 ) 2 + ( y − 1 . 5 ) 2 = 0 . 5 ⇔ x 2 − 8 y 2 − 4 x + 1 2 y = 0 , y > 0 . 7 5 ( 2 ) Solving the system of ( 1 ) and ( 2 ) , we find the coordinates of K to be ( 2 3 3 6 , 2 3 2 4 ) .
Finally, R = K I = K E + E I = ( 2 − 2 3 3 6 ) 2 + ( 0 − 2 3 2 4 ) 2 + 2 = 2 3 7 2 . For the answer, a = 7 2 , b = 2 3 , a + b = 7 2 + 2 3 = 9 5 .
Can this sum be done by Euclidean Geometry only? If so please send the solution, I'm curious.
Draw the radii and label the diagram as follows:
Then place the diagram on a coordinate plane so that C is at ( 0 , 0 ) , A is at ( 4 , 0 ) , and B is at ( 0 , 3 ) .
Then D , E , and F are midpoints of each side of the triangle, so D is at ( 0 , 2 3 ) , E is at ( 2 , 0 ) , and F is at ( 2 , 2 3 ) .
Let O be at ( p , q ) , and let the radius of the black circle be r . Then by multiple uses of the distance equation:
O G = O D + D G = p 2 + ( q − 2 3 ) 2 + 2 3 = r
O H = O E + E H = ( p − 2 ) 2 + q 2 + 2 = r
O I = O F + F I = ( p − 2 ) 2 + ( q − 2 3 ) 2 + 2 5 = r
and these three equations solve to p = 2 3 3 6 , q = 2 3 2 4 , and r = 2 3 7 2 , so a = 7 2 , b = 2 3 , and a + b = 9 5 .