Circles Geometry!

Which is larger: the yellow area or the blue area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
I love this solution. Colours really help (:
Colours are a great addition, but I wouldn't rely on it, maybe call the large circle L rather than B to avoid confusion with B .
x=r^2 π-4(r/2)^2 π+400=400
Excellent illustration...Saw this questiion back in my school days but never attempted thinking it to be real hard..LOL
great solution did it exactly the same way
Very eloquently said, Zandra.
both are equal
awesome, algebraic tricks with geometry.
I couldn't imagine this type of solutions,so I wondered by this solution. I love it.
nicely explained solution...
The answer given is sadly wrong. There is an infinitely greater amount of yellow present than blue - which is totally absent. The "blue" is in fact, cyan - the subtractive primary that absorbs red. Yellow is the subtractive primary that absorbs blue. (I know, I know....)
Log in to reply
After entirely too much effort, I would like to say that the colour is something along the lines of #3c97f2. This is a shade of azure, but it would not be incorrect to call it blue.
Very Elegant
Excellent and very clear complete solution - well done.
Please, how did you simplify or reduce "B + Y = 2Y" to "B = Y" ?
I appreciate your answer, but the first statement is an assumption... You cannot assume that each small circle's diameter is half the radius of the big circle, because there is not enough information to determine that. Without that information, you can't really solve it that way I don't think? please correct me if I'm wrong.
Log in to reply
hey bro picture clearly shows that the radius of small circle is definitely half from large circle there is no confusion in this
Log in to reply
"Hey bro" there's nothing saying it's half the diameter of the big circle, you cannot make that assumption when one of the small circles could be a little less than half the diamet of the big circle and the other one could be a little more than half. Nothing says all the small circles are "congruent" as they say in geometry.
Log in to reply
@Filipe Ferro – however though, supposing that the four small circles are not congruent, then the small circles would not exactly meet at one point. And that's not what we could see in the fig.
@Filipe Ferro – Well, to be fair, we kinda have to assume that the small circles are all congruent because there are no set measurements to determine otherwise, so if they weren't all congruent then it wouldn't necessarily be possible to give a correct answer because assuming difference in size could sway the answer either way, and since there seems to be no set numbers to give an incongruency any meaning, the answer formed by reasonable deduction would be that the colors are equal.
Log in to reply
@Herbert Stewart – I agree with that. I was just pointing it out o_o not trying to start an argument but it looks like I kind of did... I guess I know what NOT to say next time... lol
Log in to reply
@Filipe Ferro – Oh no. I'm not arguing, I just stating my opinion on the matter. Sorry if I came off as aggressive.
@Filipe Ferro – This would make it entirely unsolvable though. His assumption is based on the idea that this question has an achievable answer. Since "Impossible to solve" is not listed as an answer, his assumption is sound.
Is forma simetry
Log in to reply
The statement is about the radius not the diameter of a small circle being half the radius of the large circle. That is obvious if the point at which the small circles touch (not intersect) is the centre of the large circle. For it to not be true, a meeting point would have to be away from the centre of the large circle, and for that scenario you can only have two small circles that both touch each other and the circumference of the large circle and there would obviously be no yellow areas.
Hi @Filipe Ferro,
It is not an assumption, use the formula for area of circle, its simple dude (I too thought it was wrong)
Thank you.
Each small circle has 1/4 the area of the big circle, so their total area is equal to that of the big circle. Thus, the area of their over lap (yellow) must be equal to the area that is in their complement of the big circle (blue). That is, for all area lost by them overlapping, that area shows up in the blue region.
This gets to the heart of the matter.
This is a great geometric perspective of the algebraic approach in the top solution.
This one is the best of the lot. Congratulations Caroline'
That was my instinct but not able to verbalise it. Thanks Caroline.
Very good reasoning
Wonderfully simple reasoning! Congratulations!
perfect solution
How do we know each small circle has 1/4th of the area of the big circle?
Log in to reply
Let small circle radius be r. Then large circle has radius 2r. Area if large is 2^2 bigger since area goes with the square of the radius.
This is really good reasoning. I did it in the fashion of the above answer, but your answer is a level above in abstract reasoning. I love it.
pure reason. very nice👍🏻
Very nicely and easily explained. No confusion at all, it is a very simple way to get to the answer except the complete ones given by others. Loved it!!
I just solved it using intuition. Blue areas look like the inverse of yellow areas.
Me too. I was too lazy to do the math.
So you would be fooled by every optical illusion like the old one of the parallel lines that look curved!
Such problems almost always have an equal area
The blue area can be found by realizing that it is the difference between the large circle and (the sum of the 4 small circles minus the overlap). The overlap meaning the yellow part.
In other words, we can write:
Ar(blue)=Ar(Large Circle)-Ar(4 small circles –overlap)
Ar(blue)=Ar(Large Circle)-Ar(4 small circles) + Ar(overlap)
Let us assume that the radius of the small circle is r. Then the area of the larger circle would be 2r. Ar(blue)=pi(2r)^2 – 4 (pi r^2)+ Ar(overlap)
Ar(blue)=pi 4 r^2 – pi 4 r^2)+ Ar(overlap)
Ar(blue)=Ar(overlap)
Ar(blue)= Ar(yellow)
Hence both are equal.
Assign to each point in the large circle a number that tells you how many small circles cover that point. This number is 2 in the yellow regions, 1 in the red regions, and 0 in the blue regions. The average value of this number across the whole circle must be exactly 1, because the area of the four small circles is exactly the same as the area of the big circle (because each small circle has half the diameter of the big circle, and area scales as the square of length). The only way this can happen is if the area of the blue regions is exactly the same as the area of the yellow regions.
Lets' assign one unit to the radius of each of the 4 circles. 1) The yellow area (4 lens-spaped regions) is 2(π-2) (See http://mathworld.wolfram.com/Circle-CircleIntersection.html ). 2) The radius of the big circle (circumscribing the 4 circles) is double of the radius of each of the 4 circles, so its area is π2^2 = 4π . 3) The total area of the 4 small circles is 4πr^2 = 4π . 4) The blue area is the area of the blue circle minus the area of the 4 small circles plus the yellow area, i.e. 4π - 4π + 2(π-2) = 2(π-2) , i.e. same with the yellow area.
B l u e = C i r c l e B i g − ( 4 × C i r c l e S m a l l − Y e l l o w )
B l u e − Y e l l o w = C i r c l e B i g − 4 × C i r c l e S m a l l
B l u e − Y e l l o w = ( 2 R a d i u s S m a l l ) 2 × π − 4 × R a d i u s S m a l l 2 × π
B l u e − Y e l l o w = 4 × R a d i u s S m a l l 2 × π − 4 × R a d i u s S m a l l 2 × π
B l u e − Y e l l o w = 0
I note that the area of the blue areas is equal to the area of the large circles minus the 4 smaller circles, then adding in the yellow areas: πr² - 4π( 2 r )² + Yellow = Blue
It appears that πr² - 4π( 2 r )² = 0. thus Yellow = Blue.
Note: This is my first time making a solution guide on Brilliant, apologies if it seems confusing.
Assume that radius of small circle is 2, radius of bigger circle is therefore 4; If area of each yellow region is "a" and area of each blue region is "b" then area of the four overlapped smaller circles is 4(4 Pi) - 4a = 16 Pi - 4a
Area of the bigger circle = Pi (4)^2 - 4 b = 16 Pi - 4b
the two areas are the same; therefore 16 Pi - 4a = 16 Pi - 4b; hence a = b; QED
Use inclusion-exclusion :
The (area of the big circle) equals (the sum of the areas of the four small circles) - sum of areas of intersection (the yellow area) + area not in four small circles (the blue area).
Let A ( B ) , A ( Y ) denote the areas of the blue and yellow areas, respectively. If r = radius of small circle, then 2 r = radius of big circle. Then
( 2 r ) 2 = 4 ∗ r 2 − A ( Y ) + A ( B )
Simplify:
A ( Y ) + 4 r 2 = 4 r 2 + A ( B )
Subtract 4 r 2 from each side...
A ( Y ) = A ( B )
Really I'm love this type of problem ..and I want to more problems
... I just looked at the yellow, looked at the blue, saw the same amount of each color, chose equal amount of both as my answer
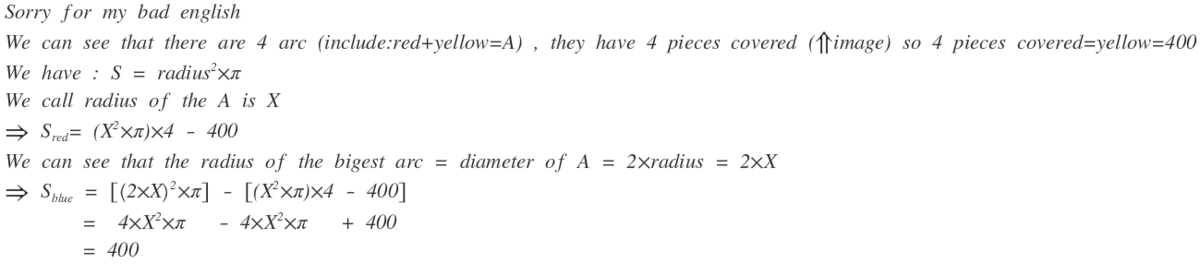
First, compare the big circle to the small circles in the figure. If we say that the radius of each small circle is r , than the radius of the big circle is 2 r . So the area of the big circle, B is 4 times the area of each small circle, S :
B = π ( 2 r ) 2 = 4 π r 2 = 4 S ( 1 )
Now, lets use the symmetry of the figure. We're given that one of the four equal yellow pieces has area Y . Let's also name each of the four symmetric blue pieces , B and each red piece , R .
Now we can construct each type of circle out of the y e l l o w , r e d , and b l u e pieces:
Each small circle, S is made out of 2 yellow pieces and 1 red piece, so: 2 Y + R = S ( 2 )
The large circle, B is made out of 4 blue pieces 4 red pieces, and 4 yellow pieces, so: 4 B + 4 R + 4 Y = B ( 3 )
Combining all three equations together:
4 B + 4 R + 4 Y B + R + Y B + Y B = = = = B = 4 S S = 2 Y + R 2 Y Y So the blue area is the same as the yellow area.