Circles in a Pinwheel
The blue circle has a radius of length 1.
The four red circles each have a radius of length 2.
What is the side length of the large, outer square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Can you give more detail on why the green segments in the diagram equal x+2? I don’t understand how you arrived at that.
Log in to reply
We know the short leg is x + 2. (The 2 there being from the radius of the red circle.)
The longer leg is 2 more than the short leg (from that first diagram), so is (x + 2) + 2. Since 2 is used up by the radius of the red circle (marked in purple) that means the remaining green part is (x + 2) + 2 - 2 = x + 2.
Log in to reply
Can you go through the Pythagorean part, I keep getting a wrong answer.
Log in to reply
@Omichael Tmichael – ( x + 4 ) 2 + ( x + 2 ) 2 x 2 + 8 x + 1 6 + x 2 + 4 x + 4 2 x 2 − 4 x − 1 6 x 2 − 2 x − 8 ( x − 4 ) ( x + 2 ) x = ( 2 x + 2 ) 2 = 4 x 2 + 8 x + 4 = 0 = 0 = 0 = 4 , − 2
Consider the original diagram, and focus on just the five circles. Their arrangement is not only rotationally symmetric, but also mirror symmetric. The following diagram shows how the lines of the original diagram fit in when reflected: the dashed blue lines. It is now clear that the square is two red (large) diameters and one blue (small) diameter wide:
2
(
2
+
1
+
2
)
=
1
0
.

To verify that this can be achieved, the calculations yield that the scenario arises by placing 4 right triangles with length 6-8-10 around a square of side length 2.
You could also solve this problem by finding the distance from one side to another by adding the diameter of the red circle, then the blue circle, then the last red circle, as if passing them on your trip from one side to the other. 4+2+4=10
Log in to reply
Can you elaborate? I think you're making an assumption about the tangents.
if you just look across the square you can see the circles do not overlap and when aligned, they make the entire length of the square. All you had to do was add up the diameters of 2 of the big circles and the small one.
How do you know that aligning them will be exactly the length of the side of the square? The way the problem has been rewritten, with only a few choices, it is possible to guess, true, but if you were to actually solve the problem, how would you do it?
Log in to reply
Exactly. In my secondary school days, I once had an exercise to determine the measures of angles in a diagram of a circle with lines in it. I had tried angle chasing but got stuck, and ended up just measuring the angles. The teacher basically told me I can't do it that way. (It turned out that I was missing just one of the relevant theorems from my repertoire - that of the cyclic quadrilateral.)
(Of course, another problem with trying to solve geometric problems in this way is that the diagram might not be to scale.)
Log in to reply
This is not a solution, it is a work-around - basically a guess. The original version of this problem, the one I posted as opposed to what became of it after the Brilliant staff got done with it, had the answer as a number rather than a multiple guess, and the number was allowed to have decimal places. Your procedure would not have been nearly as good at determining the answer in that scenario.
If i had used that explanation in a math test i would have gotten 1 point for the right numerical solution, but missing 9 for the lack of a real derivation... Our teachers drilled in our heads that measurements are always flawed :D
Log in to reply
However, it is just possible that there is an idea in this, that the aligning is not a coincidence and an actual, and elegant, proof based on it can be made.
Log in to reply
Sure, it might be possible. But this answer doesn't do it, merely asserts it.
Yeah, I also just eyeballed it. Hurray for multiple choice!
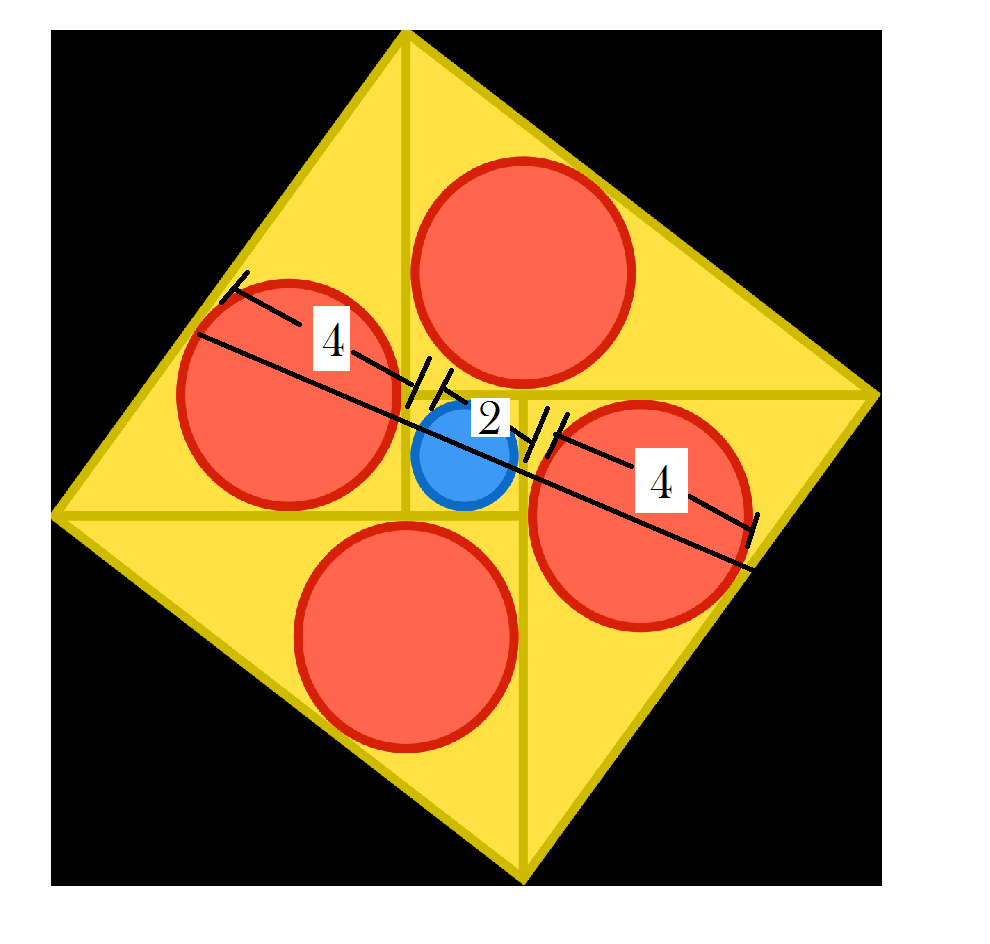
This way we can just see by adding the diameters of respective circles.
.'. Side length = 4+2+4 = 10.
There may be a way to prove this with another step but the circles are not tangent to each other so it is not clear that when added they equal the side of the square.
We know that radius of incircle of a right angle triangle is (a+b-c)/2 where a and b are perpendicular and base and c is hypotaneous .In the triangle the inradius is 2 cm . therefore a+b-c = 4 . Now we need to find a pythagorean triplet where a+b- c =4 .the triplet is 6, 8 ,10.The side of square is the hypotaneous of the triangle therefore the side =10
I think this geometric shape is not built just like that ... [maybe it's wrong or I did not understand something!]
Look at any of the right triangles.
Take its length and bredth 'a'and 'b'.
(which are clearly natural numbers.)
(area of larger square)=(area of small square)+(area of 4 triangles)
i.e. a²+b² = 4 + 2ab
Simply..... a = b + 2 so... that's it... When do u get..... (b+2)²+b² as a perfect square? Yes! When b=6
First of all the fig/question is wrong according to the geometry as it must only make 90• with diagonals intersection only .... However, if we draw perpendicular from the side of squad such that it passes through the center of circle. For understanding you may do this from all sides (with touched circle). Now watch the figure again... Do not get confused with the width of line (we can use , as it is used in the question)... By anylisia we can she that the side account for the two circle an the smaller one...
What you are doing is ballpark figure guessing rather than actual mathematical calculation. How do you know that it actually lines up?
I solved by area method. If X is side of larger square, {½ X (2+2√2)}*4 + 2² = X²
The right solution is not in the choices. The right one is 4+4*(2)^(0.5) which almost equals to 9.66. So think about it again!
Using the given information and the diagram I obtained:
( m + 2 ) 2 + m 2 = ( 2 m − 2 ) 2 ⟹ 2 m ( m − 6 ) = 0 , m = 0 ⟹ m = 6 ⟹ 2 m − 2 = 2 ( 6 ) − 2 = 1 0 .
Can someone please inform me what program to use to draw the diagrams and whether it is available for free online.
I make my diagrams using Microsoft Word. Some of the others use Figma. But even Paint can be enough.
I mainly use OpenOffice Draw, which is free.
Log in to reply
I wanted something free. Thanks. I'm going to look into it now. I use free programs such as Microsoft Visual Studio and Free Pascal, but I will take whatever I can get for free. Unfortunately, using the two free programs above, I cannot use anything I create outside of the program environment.
Thanks again.
I got the answer a bit differently. I thought of a formula for finding the radius of a circle inscribed in a triangle. The formula states that 2A/P = r, where A is the area of the triangle, P being the perimeter, and r being the radius. Since the circle in the triangles have the radius is 2, we can say that 2A/P = 2, which then simplifies to A/P = 1. That means the area of the triangle and the perimeter is equal, and i know the only triangle that is possible is 6 by 8 by 10 triangle. Since the edge of the square is the hypotenuse, i know 10, the largest side must be the side length of the square.
Your equation is necessary but not sufficient. There are other right triangles for which A = P . For example a = 1 0 , b = 3 1 6 .
In fact any triangle with legs satisfying the equation a + b = 4 a b + 2 will have A = P , but generally it will not have a hypotenuse equal 10. The one in this example has c = 3 3 4 .
We know the side of the large square is the hypotenuse of a right triangle and 10 is the only valid hypotenuse of a Pythagorean triple.
This assumes that the puzzle creator specifically selected an integer solution.
I just looked from the side and saw that the lenght is 2 red balls plus 1 blue ball. So 4+4+2.
Since the side of the large square is also the hypotenuse of a right triangle, its square must be the sum of two squares. Thus, the correct answer is 10.
I don't get where you got the numbers.
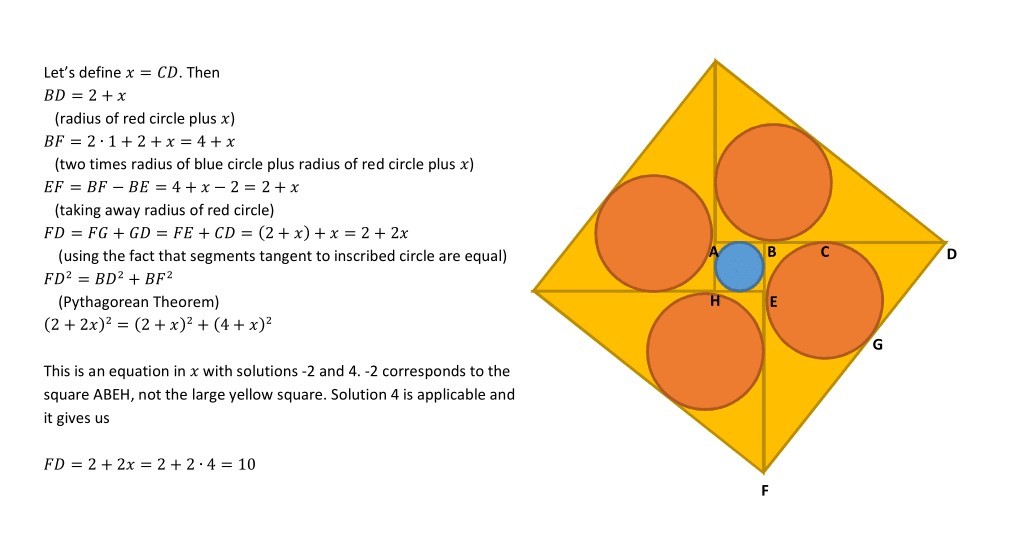
(This proof is roughly the same as Marta's, but with a less symbolic presentation.)
We know (from the diagram above) that the the longer leg of the right triangle must be 2 more than the shorter leg of the triangle.
We know the marked black line segments are congruent and the marked green line segments are congruent due to them being tangent line segments to a circle.
In addition, if the black line segment length is x , the green one is x + 2 (since the longer leg is 2 more than the shorter, and the remaining part of both sides are congruent lengths of 2).
Using the Pythagorean Theorem obtains the formula ( x + 2 + 2 ) 2 + ( x + 2 ) 2 = ( x + x + 2 ) 2 . Solving for x gets values of 4 and -2, although only the positive one makes sense in context. So the hypotenuse is x + x + 2 = 4 + 4 + 2 = 1 0 which is the same as the side of the square.