Circles In Circle
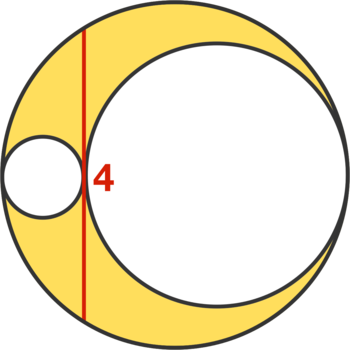
In a large circle, a chord of length 4 is drawn.
Then, as shown above, we draw in two small circles that are each tangent to the large circle and to the midpoint of the chord.
What is the area of the yellow region?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The solution looks slightly more elegant/symmetric if you express the lengths in r S and r L :
∣ A B ∣ 2 = ∣ O A ∣ 2 − ∣ O B ∣ 2 = ( r S + r L ) 2 − ( r S − r L ) 2 = ( r S 2 + 2 r S r L + r L 2 ) − ( r S 2 − 2 r S r L + r L 2 ) = 4 r S r L ,
and the area is
π ( ( r S + r L ) 2 − r S 2 − r L 2 ) = π 2 r S r L ,
and since 4 r S r L = 2 2 = 4 , the area is 2 π .
I was surprised that the answer only depended on the length of the chord.
It reminded me of the area of the annulus question, which was much easier to see why. Is there a similar intuition for this problem?
Log in to reply
I was surprised at the result too. with a being the chord length we find that r S r L = 4 a 2 , giving an area for the yellow region of 2 π r S r L = 2 1 π a 2 . I'm working on the intuition part ....
Log in to reply
I only wonder: why can we say with certainty that rs + rl = R.(Sorry for notation, mobile user)
Log in to reply
@Peter van der Linden – Good point. I assumed from the drawing that the point of tangency was at the midpoint of the chord, but this is not explicitly stated. If it is the midpoint then of course
2 r S + 2 r L = 2 R ⟹ r S + r L = R .
As presently stated we could have any number of possibilities, so I will add this condition.
@Chung Kevin I hope that adding the "midpoint" clarifier is in line with what you intended.
Log in to reply
@Brian Charlesworth – I initially used semicircles (similar in image to other problems that I was working on) when I found out this fact. I then converted it into a circle to look nicer, but forgot to add in all of the information. Thanks for helping me out.
Sir .. thanks for such a nice question :)
Mr. Kevin, yes, I remember the annulus question as well. The one with the 18cm chord.
Let me know if the way I solved this problem is acceptable. I start by looking at the data given and the answer asked for. And, if the problem is in principle correct, and if the answer "insufficient data to solve" is not right, then I assume that the yellow area is invariant, irrespective of the position of the point of tangency. That is, irrespective of how large/small the two inner circles are, the value of the yellow region is going to be the same. Now, I try to check it for an "easy case" - where the chord is actually the diameter of the main circle. In that case, the yellow area = pi x 2 x 2 - 2(pi x 1 x 1) = 4pi - 2pi = 2pi.
Is this acceptable?
Log in to reply
The problem with your approach is that you have not ruled out "insufficient data to solve". A complete solution will prove that the answer applies for all possible chords.
Log in to reply
That's why I phrased the last option as "depends on the ratio", which prevents checking on easy cases.
You're a loser best go play with your grandchildren old man
We could use property of relation between chord length and diameter this also explains area depends on chord. I have image explaning solution but i don't see any options for uploading it.
maybe oversimplified but if the chord can be anywhere then if it was down the middle of the large circle and the inscribed white circles were identical then the area of the yellow circle is 4 PI and each of the white circles is PI so the yellow area is 4 PI - 2 PI = 2 PI
Ideally, the solution should prove the general case, and not just a specific scenario with a simplifying assumption to calculate the answer. (Yes, that's a limitation of such a numerical answering system.)
Let R be the radius of the outer circle and r S , r L be the radii of the smaller and larger interior circles, respectively. Then r S + r L = R ⟹ r L = R − r S .
Now let O be the origin of the outer circle, A the lower end of the chord and B the midpoint of the chord. Then ∣ O A ∣ = R , ∣ O B ∣ = R − 2 r S and ∣ A B ∣ = 2 . By Pythagoras we then have that
∣ O A ∣ 2 = ∣ O B ∣ 2 + ∣ A B ∣ 2 ⟹ R 2 = ( R − 2 r S ) 2 + 2 2
⟹ R 2 = R 2 − 4 R r S + 4 r S 2 + 4 ⟹ R r S − r S 2 = 1 .
Next, the area of the yellow region is
π R 2 − π r S 2 − π r L 2 = π ( R 2 − r S 2 − ( R − r S ) 2 ) =
π ( R 2 − r S 2 − R 2 + 2 R r S − r S 2 ) = 2 π ( R r S − r S 2 ) = 2 π × 1 = 2 π .