Circles, Tangents, And Triangles (Oh My...)

Let the blue tangent intersect the red circle at B, let the red tangent intersect the blue circle at C.
Let the center of the red circle be X and the center of the blue circle be Y.
We are given $m\angle BP_1C = 90^\circ .$
Adding the sides and angles as indicated on the diagram, $m\angle 1 + m\angle 2 = 90^\circ .$

Lemma 1: $P_1P_2 B$ is a right triangle
Since the blue tangent is perpendicular to the red tangent, hence the blue tangent passes through the center of the red circle and $P_1 B$ is the diameter of the red circle. Thus $\angle P_1 P_2 B = 90 ^ \circ$ .

Lemma 2: $B P_2 C$ is a straight line.
We already have $\angle P_1 P_2 B = 90 ^ \circ$ . Similarly, $\angle P_1P_2 C = 90 ^ \circ$ . Thus, $B P_2 C$ is a straight line.

Lemma 3: $P_3 P_2 P_4$ is a straight line.
Triangles $XP_2 P_1$ and $X P_2 P_3$ are congurent (SSS), hence $\angle P_1P_2P_3 = 2 \angle XP_2 P_1$ .
Similarly, Triangles $YP_2 P_1$ and $Y P_2 P_4$ are congurent (SSS), hence $\angle P_1P_2P_4 = 2 \angle YP_2 P_1$ .
Since $XP_1 Y P_2$ is a kite, hence $\angle XP_2 Y = \angle XP_1 Y = 90 ^ \circ$ .

Thus, $\angle P_1 P_2 P_3 + \angle P_1 P_2P_4 = 2 ( \angle XP_2 P_1 + \angle Y P_2 P_1 ) = 2 ( \angle XP_2 Y) = 180^ \circ$ .

Lemma 4: $P_3 P_1 P_4$ is a right triangle.
$\angle P_3 P_1 B = \angle P_3 P_2 B = \angle P_4 P_2 C = \angle P_4 P_1 C$ .
Hence $\angle P_3 P_1 P_4 = \angle P_3 P_1 B + \angle BP_1P_4 = \angle P_4 P_1 C + \angle BP_1 P_4 = \angle BP_1 C = 90 ^ \circ$ .

Finally, we are ready to do the calculations:

$m\overline{P_1P_2} = m\overline{P_1B} \cdot m\overline{P_1C} / m\overline{BC} = 6 \cdot 8 / 10 = \frac{24}{5}$

$\sin(\angle 1) = \cos(\angle 2) = \frac{3}{5}$

$\cos(\angle 1) = \frac{4}{5}$

$m\overline{P_1P_3} = 2 \cdot m\overline{P_1P_2} \cos(\angle 2) = \frac{144}{25}$

$m\overline{P_1P_4} = 2 \cdot m\overline{P_1P_2} \cos(\angle 1) = \frac{192}{25}$

$m\overline{P_3P_4} = 2 \cdot m\overline{P_1P_2} = \frac{48}{5}$

Then the altitude of the triangle $P_3P_1P_4$ is $m\overline{P_1H} = m\overline{P_1P_3} \cdot m\overline{P_1P_4} / m\overline{P_3P_4} = \frac{576}{125} .$

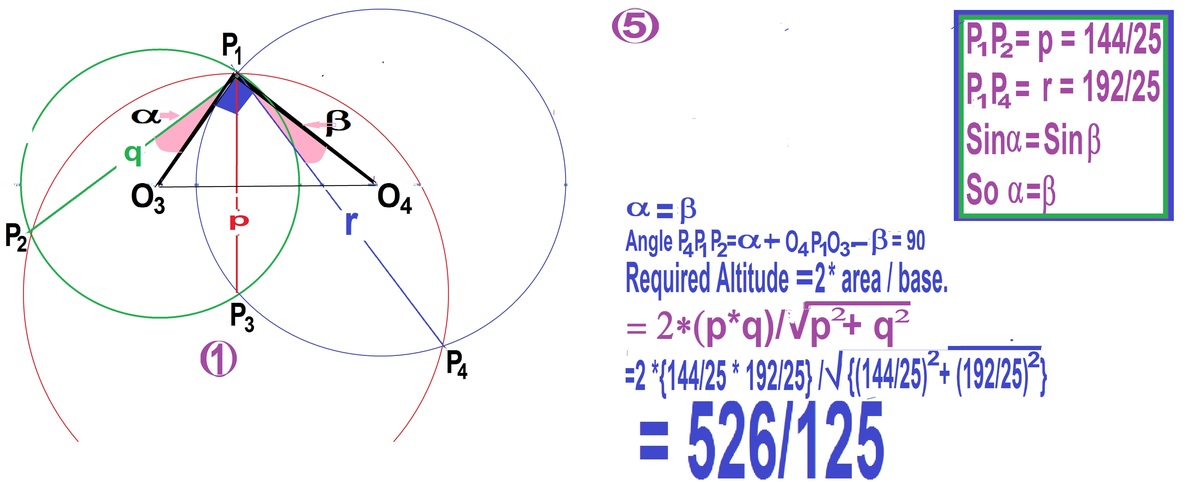
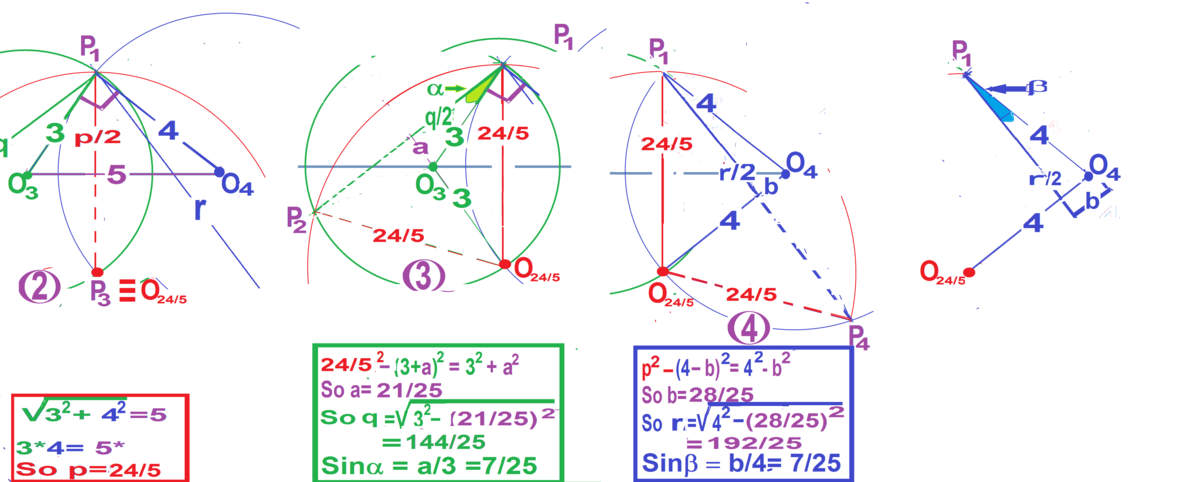
$Please\ see\ the\ Fig.\\ Fig.\ 1 \ shows\ the\ problem. \ \angle \ O_4P_1O_3\ is\ given\ as\ 90^o. \\ Fig.\ 2\ finds\ out\ the\ length\ of\ P_1P_3=p=\frac {24}{5} \\ Fig.\ 3\ finds\ out\ the\ length\ of\ P_1P_2=q=\frac {144}{25} \\ , \ \ \ and\ \ Sin\alpha .\\ Fig.\ 4\ finds\ out\ the\ length\ of\ P_1P_4=r=\frac {192}{25} \\ , \ \ \ and\ \ Sin\beta.\\ Fig.\ 5 \ at\ top\ right \ gets\ the\ answer.$

All three solutions Fig. 2 to Fig. 4 are based on properties of isosceles triangle and its half as a right triangle.

If you are comfortable,use co ordinate geometry to do easily.

Let, P1(0,0) Notice, the centre of the circle of radii 4 lies on the tangent of circle of radii 3 and its centre is C1(4,0) Similarly the centre of the circle of radii 3 lies on C2(0,3)

Note P1P2=24/5 ( easy to evaluate)
It is also the radii of circle with centre P2.



 Equation of circle with centre C1,C2,P1 are respectively

  1).    (x-4)^2+y^2=4^2
  2).     x^2+(y-3)^2=3^2
  3).     x^2+y^2=(24/5)^2

Solving 1) and 3 ) we get a value of P3(72/25,-96/25)

Solving 2) and 3) We get P4(-72/25,96/25)

*Equation of P3P4=100x-75y-576=0
Perpendicular from P1(0,0) is

P=|100(0)+(-75)(0)+(-576)|/√(100^2+75^2)

   =576/125☺☺☺