Circular Accelerometer
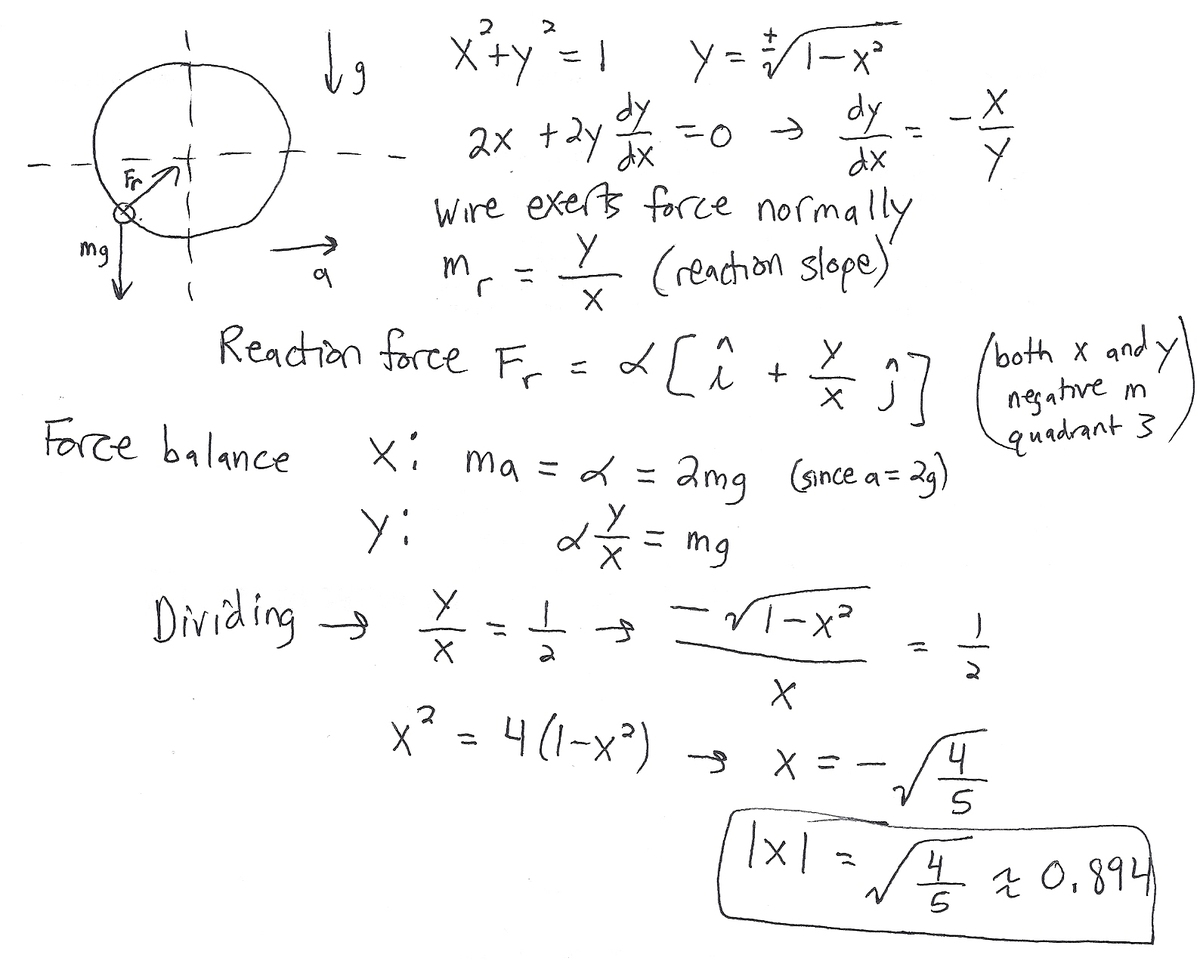
A bead is positioned on a friction-less circular wire with a radius of 1. There is a uniform downward gravitational acceleration g .
The horizontal acceleration of the wire is a ( = 2 g ) . Determine the location on the wire at which the bead could be placed, such that it would remain at rest relative to the ring. Give your answer as the horizontal distance from this location to the wire's vertical axis of symmetry.
The answer is 0.894.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I had a doubt. Please help, if you don't mind. Can we say that the bead here experiences centripetal (or as a consequence centrifugal) force? The particle here is at equilibrium, so I don't think so, but I wanted opinions.
Log in to reply
I'm not inclined to describe it that way, since there isn't really any rotation. But if you can make a case, then maybe so.
This can be very easily done. First of all , the bead is expriencing , two accelartions, 1 horizotal, 1 verital. Now By Vector Law, the resultant of the two perpendicular acceleration vectors are ( 2 g ) + ( g ) 2 = a r = g 5 .
Hence now, this acceleration is equal to the centrepetal accelaration a c = v 2 / r where r=1m
Hence a r = a c or g 5 = v 2
Hence 1/2mv^2 = mgh, now h = 5 /2 from the uppermost part of the axis.
Now it will look something like this
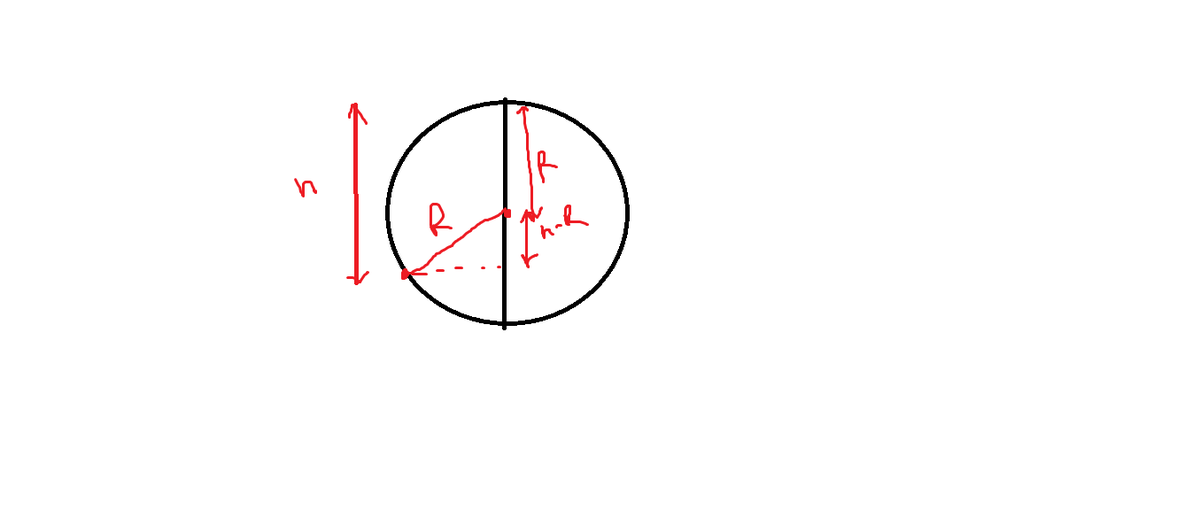
Now by pythagoras, we get Distance = 0.89.. (approx)
Interesting. You applied rotational concepts to a non-rotational problem and got the right answer. What would your answer have been if a and g were the same?
Log in to reply
Thanks let me see
Are you in fb? It is easy to discuss there
Log in to reply
No, I'm not. But for the case where a and g are the same, I get x = 1/sqrt(2). My solution is also posted above.
Log in to reply
@Steven Chase – ok. so let me check if it is coming..
@Steven Chase – is my solution wrong anywhere? I dont think so
@Steven Chase – Yes, same, i am also getting 1 / 2
Log in to reply
@Md Zuhair – We agree in both cases. I was just surprised, since it seemed like we solved it very different ways.
Referring to the figure in the text of the problem, let θ be the angle formed between the directions 1) bead-centre of the wire and 2) centre of the wire-down along the wire's vertical axis of symmetry (sorry, I am too lazy to draw).
The bead's weight generates a tangential acceleration g sin θ in the anti-clockwise sense. The acceleration of the wire generates a tangential acceleration a cos θ in the clockwise sense. Since the bead is in equilibrium, we have:
a cos θ = g sin θ
that is
tan θ = 2
Since the radius of the wire is 1, the distance of the bead equilibrium position to the vertical axis is sin θ , which expressed through the tangent gives:
sin θ = 1 + tan 2 θ tan θ = 5 2 = 0 . 8 9 4 4 2 7 . . .