Circumscribed and Inscribed Spheres.
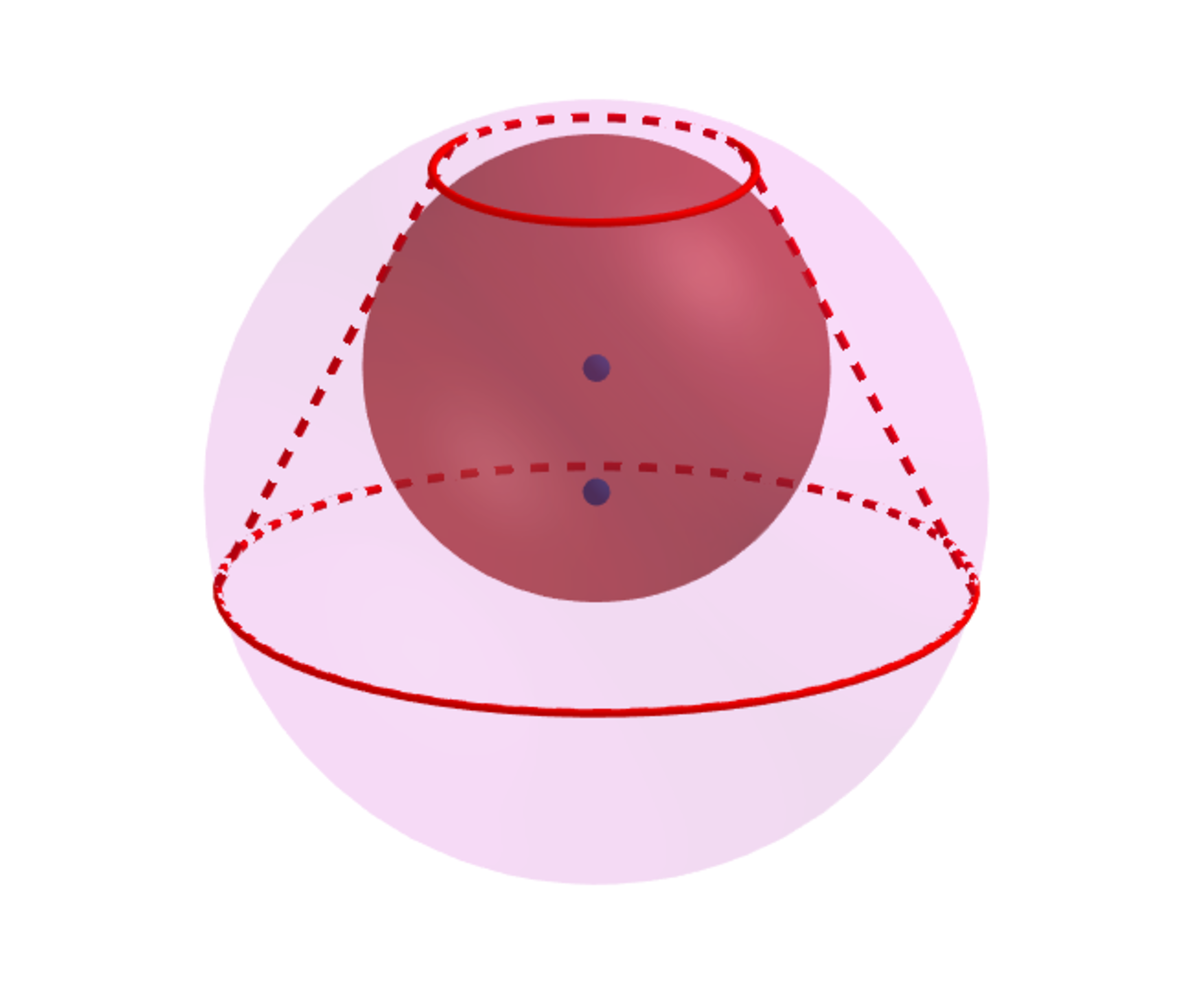
In the diagram above, a sphere is inscribed in a truncated cone such that the volume of the truncated cone is twice the volume of the inscribed sphere and another sphere is circumscribed about the truncated cone.
Let r be the radius of the inscribed sphere and R be the radius of the circumscribed sphere.
If r R can be expressed as r R = b a c , where a , b and c are coprime positive integers, find b ∗ c − a .
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I don't understand why R/r = 0.75*sqrt(5) have to be overcomplicated with all those square roots.
Log in to reply
It can be simplified to your result r R = 4 3 5 .
Log in to reply
I found the answer 4 3 5 , then most of the work was expressing it in the given unsimplified form! Nice puzzle apart from that, though.
Log in to reply
@Chris Lewis – It can be simplified to r R = 4 3 5 .
I didn't repost the problem using the simplified form since people has already done the problem.
I restated the problem as follows:
If r R can be expressed as r R = b a c , where a , b and c are coprime positive integers, find b ∗ c − a .
This way the result is 1 7 .
First we find w in terms of m using the inscribed sphere below.
Using the fact that tangents to a circle from an outside point are congruent we obtain the diagram above.
The height h of the truncated cone is h = 2 r
Using right △ A B C we have:
( w + m ) 2 = ( w − m ) 2 + 4 r 2 ⟹ w 2 + 2 w m + m 2 = w 2 − 2 w m + m 2 + 4 r 2 ⟹ 4 w m = 4 r 2 ⟹ r 2 = w m ⟹
r = w m .
The volume of the inscribed sphere V s = 3 4 π ( w m ) 2 3
and
The volume of the truncated cone is V T = 3 2 π ( w 2 + w m + m 2 ) ( w m ) 2 1
V T = 2 V s ⟹ w 2 + w m + m 2 = 4 w m ⟹ w 2 − 3 w m + m 2 = 0 ⟹ w = ( 2 3 ± 5 ) m
Since m w > 1 we choose w = ( 2 3 + 5 ) m
Next we use the circumscribed sphere to find m R .
R 2 = z 2 + w 2 = R 2
R 2 = ( h − z ) 2 + m 2
⟹ z 2 + w 2 = h 2 − 2 h z + z 2 + m 2 ⟹ z = 2 h h 2 − w 2 + m 2
Using the values for w and h above and simplifying we obtain:
z = 4 2 3 + 5 7 + 5 m
Using R 2 = z 2 + w 2 and simplifying we obtain:
R = 4 3 3 + 5 5 ( 7 + 3 5 ) m and r = w m = 2 3 + 5 m
⟹ r R = 2 2 ( 3 + 5 ) 3 5 ( 7 + 3 5 ) = 2 2 3 ( 3 + 5 ) 2 5 ( 7 + 3 5 ) =
2 2 3 2 ( 7 + 3 5 ) 5 ( 7 + 3 5 ) = 4 3 5 = b a c ⟹ b ∗ c − a = 1 7 .