Circumscribed To Infinity

Geometry Level 5

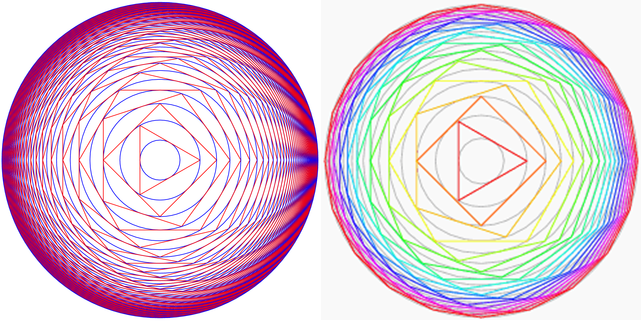Circumscribe a triangle about a unit circle, another circle around the triangle, a square outside this circle, another circle outside the square and so forth.

Let $r$ be the radius of the circle formed when the process is carried forever.

Find the square root of the sum of first 14 decimal places of $r$

You are allowed to compute the answer by calculator or software.

The answer is 7.

1 solution

Digvijay Singh
May 2, 2015

The sequence of decimal places here

Do you have a closed form for the product, or are we meant to evaluate it numerically?

D G - 6 years, 1 month ago

Yeah, we can find a closed form, but that would be very complex. The main aim of this question is to make you research and know about the On-Line Encyclopedia of Integer Sequences (OEIS). It is an online database of integer sequences, and the integer sequence of the radius is given here . I also mentioned this link in the Beginning of the solution. The website stores the integer sequence of all the major (like e, π, $\sqrt{2}$ , etc.) and minor (like ζ(3), φ, γ, etc.) constants.

Moreover, you can use Wolfram Alpha's Product Calculator

Digvijay Singh - 6 years, 1 month ago

I think it should have been mentioned that using Wolfram Alpha was permitted. I gave up because I couldn't find a closed form. :( Nice problem anyway. :)

Danish Mohammed - 6 years, 1 month ago

@Danish Mohammed – Thanks... and keep exploring... :)

Digvijay Singh - 6 years, 1 month ago

Solving this for hours then I found out that this was only a constant XD

Rindell Mabunga - 6 years, 1 month ago

Circumscribed To Infinity

The answer is 7.

1 solution

0 pending reports