Classic Geometry Problem
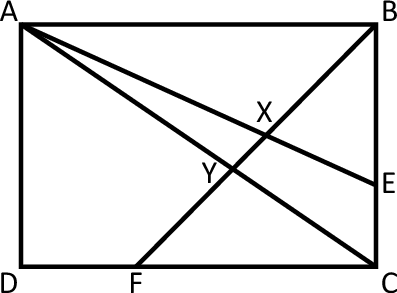 In the figure shown,
A
B
C
D
is an arbitrary rectangle. Point
E
lies on side
B
C
such that
E
C
B
E
=
2
and point
F
lies on
C
D
such that
F
D
C
F
=
2
. Segments
A
E
and
A
C
intersect
F
B
at points
X
and
Y
, respectively. The ratio
F
Y
:
Y
X
:
X
B
can be expressed as
a
:
b
:
c
where
a
,
b
, and
c
are coprime, positive integers. Find
a
+
b
+
c
.
In the figure shown,
A
B
C
D
is an arbitrary rectangle. Point
E
lies on side
B
C
such that
E
C
B
E
=
2
and point
F
lies on
C
D
such that
F
D
C
F
=
2
. Segments
A
E
and
A
C
intersect
F
B
at points
X
and
Y
, respectively. The ratio
F
Y
:
Y
X
:
X
B
can be expressed as
a
:
b
:
c
where
a
,
b
, and
c
are coprime, positive integers. Find
a
+
b
+
c
.
The answer is 65.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
i've also done in the similar manner
I tried the problem using Menalaus theorem. Please explain why the theorem doesn't hold good for this question.
65..
( link try to do this problem please
A coordinate free proof. By Tales theorem ∣ Y B ∣ ∣ F Y ∣ = ∣ A B ∣ ∣ F C ∣ = 3 2 . that is ∣ F B ∣ = 2 5 ∣ F Y ∣ .
Let G be the intersection point of lines A X and C D . Then again by Tales we have ∣ D C ∣ ∣ C G ∣ = ∣ A B ∣ ∣ C G ∣ = ∣ E B ∣ ∣ C E ∣ = 2 1 and ∣ X B ∣ ∣ F X ∣ = ∣ A B ∣ ∣ F G ∣ = ∣ A B ∣ ∣ F C ∣ + ∣ C G ∣ = 3 2 + 2 1 = 6 7 , that is ∣ F B ∣ = 7 1 3 ∣ F X ∣ . Hence we have that ∣ F X ∣ ∣ F Y ∣ = ∣ F X ∣ ∣ F B ∣ ∣ F B ∣ ∣ F Y ∣ = 7 1 3 ⋅ 5 2 = 3 5 2 6 , and ∣ F Y ∣ ∣ Y X ∣ = 3 5 3 5 − 2 6 = 2 6 9 . Now 2 3 = ∣ F Y ∣ ∣ Y B ∣ = ∣ F Y ∣ ∣ Y X ∣ + ∣ X B ∣ = 2 6 9 + ∣ F Y ∣ ∣ X B ∣ , hence ∣ F Y ∣ ∣ X B ∣ = 2 3 − 2 6 9 = 2 6 3 9 − 9 = 2 6 3 0 so that ∣ X B ∣ : ∣ Y X ∣ : ∣ F Y ∣ = 3 0 : 9 : 2 6 . As G C D ( 2 6 , 9 , 3 0 ) = 1 , we have that a + b + c = 6 5 .
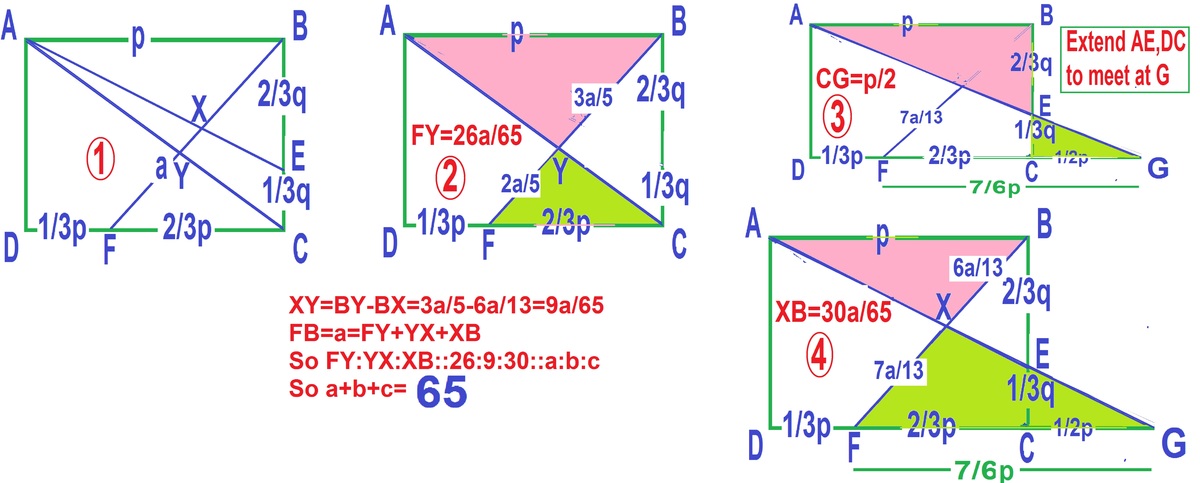
Missed it due to slip in addition!!!
Thanks for the solution.
Because A B C D is an arbitrary rectangle, let's just assume that it's a square. From here, let's let the side length be 3 . Now, we can graph this. We'll let Point D lie on the origin, and so on and so forth, such that B is located at ( 3 , 3 ) . Now, let's find the line A E . We know that length E C is equal to 1 , so E is the point ( 3 , 1 ) . Thus, the graph of the line is y = 3 − 2 x + 3 . Now let's find F B . Similarly, we can label the point F to be ( 1 , 0 ) . The graph of this line is 2 3 x − 2 3 . To find point X , let's set these equations equal. Solving, we find that X is at the point ( 5 2 7 , 5 3 3 ) . We can likewise deduce that point Y is ( 5 9 , 5 6 ) . Now, applying the distance formula, we find that the ratio is 2 6 : 9 : 3 0 , and thus the desired answer is 2 6 + 9 + 3 0 = 6 5 . And we're done! This is a really bad approach, the calculations are messy, it takes lots of time, etc., so try to find a cool way to tackle the problem. :D
finn, just write a good solution :) ppl here like me are not as good as you and calvin are. we need to know not only the answer, but also solution. it doesnt help to grow knowledge without knowing new approaches.
hope you post a solution soon :)
Log in to reply
Yeah, I guess.
Log in to reply
thanx :)
i am seriously waiting for a solution finn.. :D u hv got me waiting for 2 dys.
Log in to reply
@Nisarg Thakkar – You seriously want a solution? Fine, I'll give you one now.
Log in to reply
@Finn Hulse – :D Thanx! If never wanted a solution, I would not have commented on this problem! And if I already had a solution, I would have posted it. But thanx for sharing the solution.
Log in to reply
@Nisarg Thakkar – HAHAHAHA that is not a solution. That's a guideline. A solution should be brief as well as beautiful. I just made a really bashy solution and encouraged you guys to come up with a cool solution. :D
Problems with phrasing: "Segments A E and A C intersect at points X and Y , respectively." Intersect what? Each other? B F ? I know there is a picture, but problems should have unambiguous wordings.
And you should really add a line saying that A B C D is a rectangle. Although you can see that it looks like a rectangle, I think it'll be helpful for others.
Remember that it's an arbitrary rectangle.
@Calvin Lin Copying your style of solutions. :D
Log in to reply
Not necessarily a great idea as @Nisarg Thakkar points out. You should also provide enough steps to guide at the crux of the problem.
I like the "Treat the whole thing as a square". Can you explain why we can do that without loss of generality?
Log in to reply
Oh, yeah. Because it's an arbitrary rectangle, no matter what you do to it it the ratio will remain the same. So for some, it's easier to work with a square.
Log in to reply
@Finn Hulse – Maybe, but how do you know the ratio isn't different if it's a rectangle with unequal side lengths? While your method is indeed short and the way I would have done it had I gotten it at AMC, AIME, or some other MCQ contest, it is incomplete unless you justify this portion.
Log in to reply
@Sreejato Bhattacharya – I totally agree dude. But I'm leaving the truly beautiful part of this problem to you guys.
I feel like coordinate bash is overkilling here. It suffices to ratio chase B F F Y , B F B X using parallels.
a classic geometric sol n

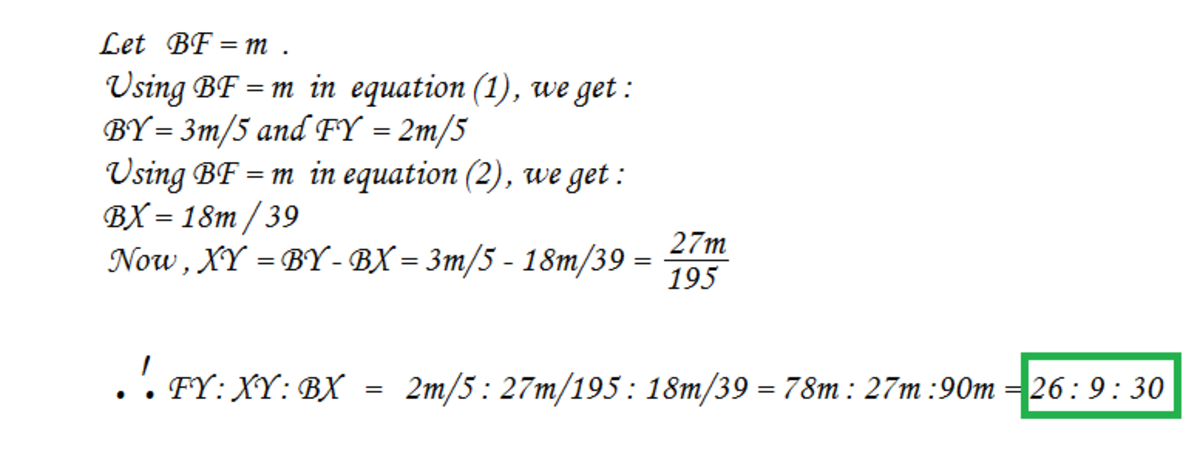 So the required answer should be ::
26+9+30 = 65
So the required answer should be ::
26+9+30 = 65
any confusions please comment
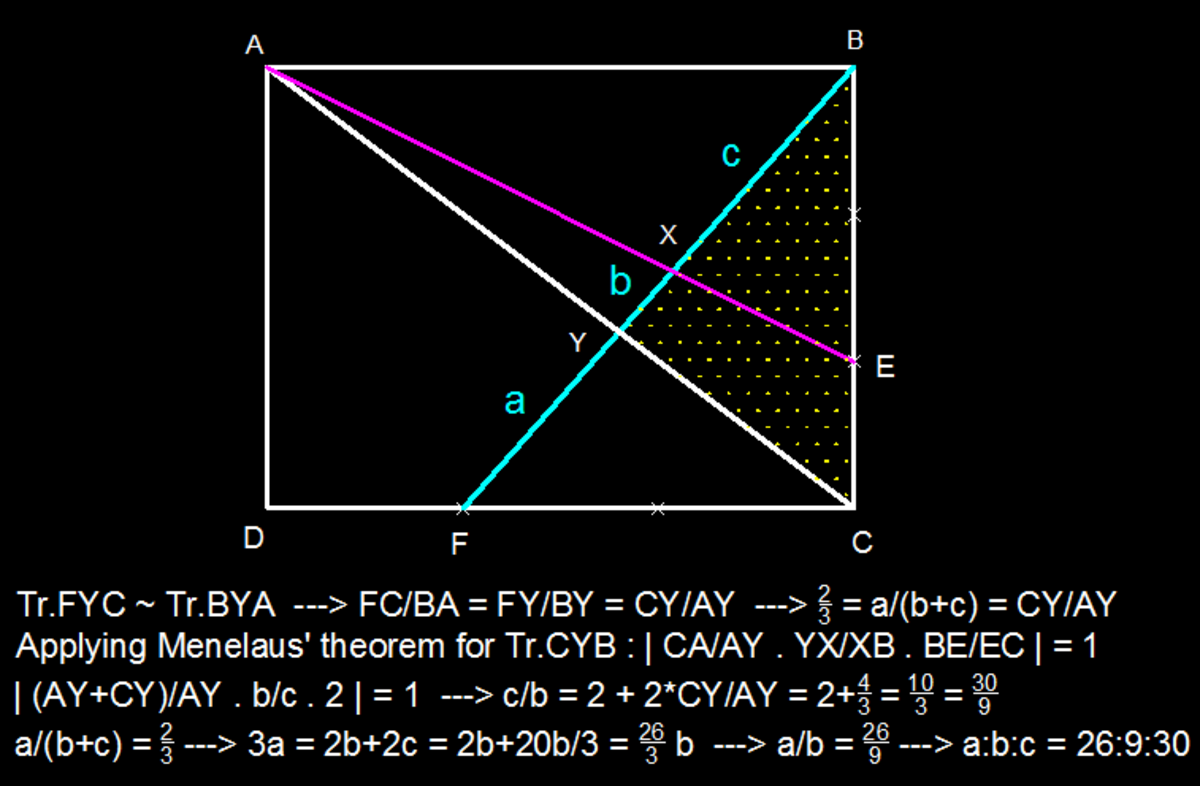
Assume that D:(0,0), A:(0,3q), B:(3p,3q) & C:(3p,0) -- a general rectangle where p. q are unknown. We find line BF to be: y=3qx/(2p) - 3q/2 and AC : x/(3p)+y/(3q)=1 which gives us Y to be: (9p/5, 6q/5). Similarly, determine X as (27p/13, 21q/13). We can now say that FY:YX:XB=(9/5 -1):(27/13 - 9/5)):(3 - 27/13) = 26:9:30