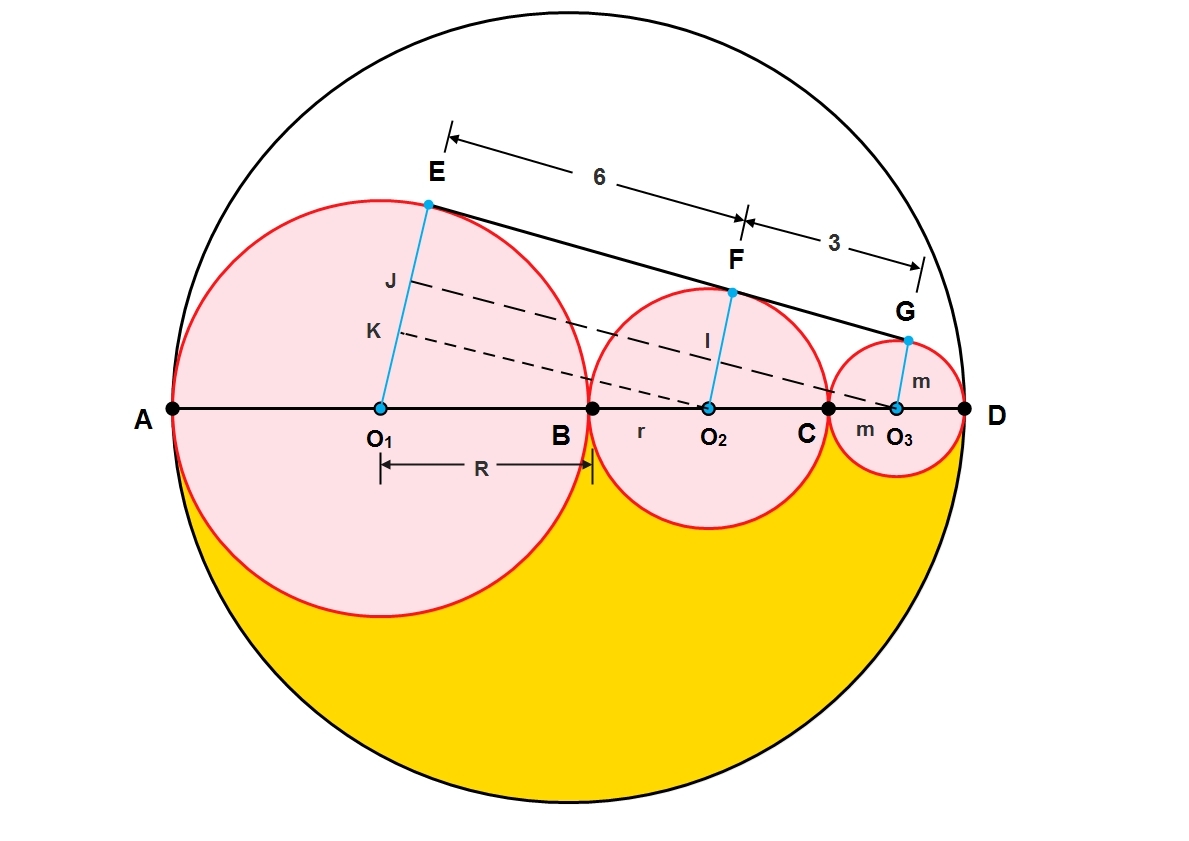
What A Weird Shape!

Imgur

We can consider this region as two 'nested' Arbeloses!

So after finding $ab=9;~~~~bc=\frac{9}{4};~~~~ac=\frac{9}{2}$ [I did not show working here as most solutions in the thread have already done it]

Area of the green Arbelos = $\pi ab = 9\pi$ . . . . see this video for what is an Arbelos and the interesting expression for its area.

Area of yellow Arbelos = $\pi c(a+b) = \pi ca + \pi cb = \pi (\frac{9}{2} + \frac{9}{4})$

Add the two for total area $A = \frac{22}{7} \times 9 (1+\frac{1}{2}+\frac{1}{4}) = \boxed{49.5}$

For another interesting property of an Arbelos see this note

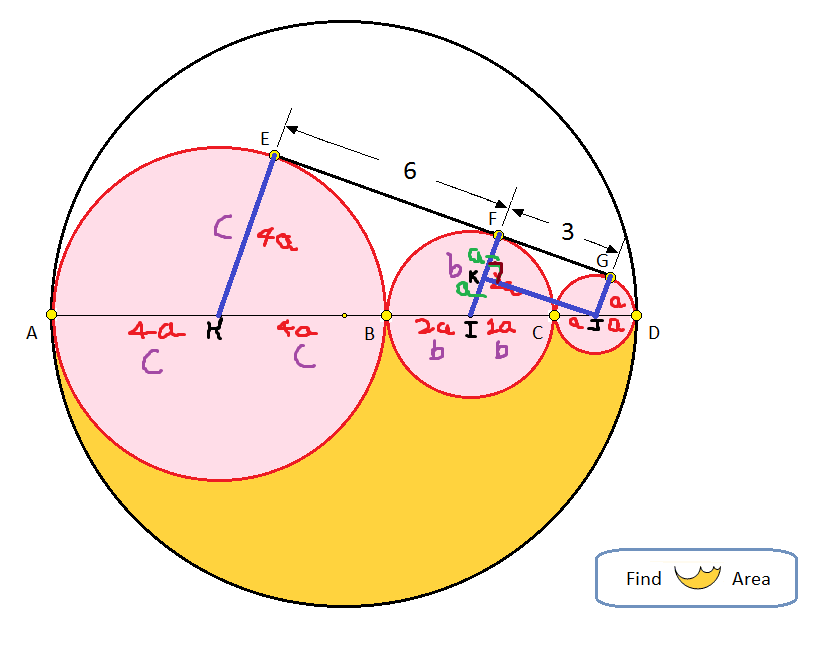
Let the radii of the circles be $a , b , c$

We know , $b = \sqrt {ac} \dots (1)$

Also , similarity gives us -

$\frac{GF}{FE} = \frac{JI}{IH} \Rightarrow \frac{3}{6} = \frac{a + b}{b + c)} \Rightarrow \frac{3}{6} = \frac{a + b}{b + c)}$

This relation gives us $2a + b = c . . .(2)$

Also , $[GJHE] = [GJIF] + [FIHE]$

$\Rightarrow \frac{1}{2}(a + c)(9) = \frac{1}{2}(a + b)(3) + \frac{1}{2}(b + c)(6)$

After simplifying this , we get $c = 3b - 2a . . .(3)$

Equating $(2) , (3)$

$2a + b = 3b -2a \Rightarrow b = 2a$

From relation $(1)$ and $b =2a$ , we get , $c = 4a$

Also , Area of shaded region $= \frac{1}{2}\times \frac{22}{7}(7a)(7a) - \frac{1}{2} \times \frac{22}{7}(4a)(4a) - \frac{1}{2} \times \frac{22}{7}(2a)(2a) - \frac{1}{2} \times \frac{22}{7}(a)(a)$

$= 77a^2 - \frac{11}{7}(16a^2 + 4a^2 + a^2)$

$= 77a^2 - 33a^2$

$= 44a^2$ .

Let $JK \perp FI$ giving us $\Delta JKI , JK = 3 , KI = a , JI = 3a$

Using Pythagoras theorem , $9a^2 = 3^2 + a^2$

$8a^2 = 9$

$a =\frac {3(\sqrt {2})}{4}$

So , area of shaded region = $44a^2 =44(\frac {3(\sqrt {2})}{4})^2 = 44 \times \frac{18}{16} = \frac{99}{2} = \huge \boxed{49.5}$

Using similar logic as Banti Paswan , maybe shorter solution. Let the radii of circles AB, BC and CD be $r_3$ , $r_2$ and $r_1$ respectively. Using Banti's diagram, we notice that:

$\begin{cases} O_2O_3^2-O_2N^2 = O_3N & & \\ \quad \Rightarrow (r_2+r_1)^2-(r_2-r_1)^2=3^2 & \Rightarrow 4r_1r_2 = 9 &...(1) \\ O_1O_2^2-O_1P^2 = O_2P & & \\ \quad \Rightarrow (r_3+r_2)^2-(r_3-r_2)^2=6^2 & \Rightarrow 4r_2r_3 = 36 &...(2) \\ O_1O_3^2-O_1Q^2 = O_3Q & & \\ \quad \Rightarrow (r_3+2r_2+r_1)^2-(r_3-r_1)^2=(3+6)^2 & = 81 &...(3) \end{cases}$

From Eqn 2 $\div$ Eqn 1: $\Rightarrow \dfrac {r_3}{r_1} = 4 \quad \Rightarrow r_3 = 4r_1$ . Substituting this in Eqn 3:

$\begin{aligned} (r_3+2r_2+r_1)^2-(r_3-r_1)^2 & = 81 \\ (5r_1+2r_2)^2 - (3r_1)^2 & = 81 \\ 16r_1^2 + 20r_1r_2 + 4r_2^2 & = 81 \\ 16r_1^2 + 5(4r_1r_2) + 4r_2^2 & = 81 \\ 16r_1^2 + 5(9) + 4r_2^2 & = 81 \\ 16r_1^2 + 4r_2^2 & =36 \\ 4r_1^2 + r_2^2 & = 9 \\ 4r_1^2 + r_2^2 & = 4r_1r_2 \\ 4r_1^2 -4r_1r_2+ r_2^2 & = 0 \\ (2r_1-r_2)^2 & = 0 \ \end{aligned}$

$\Rightarrow r_2 = 2r_1 \Rightarrow 8r_1^2 = 9 \Rightarrow r_1 = \dfrac {3} {\sqrt{8}} \Rightarrow r_2 = \dfrac {6} {\sqrt{8}} \Rightarrow r_3 = \dfrac {12} {\sqrt{8}}$

The area of the orange shaded region is given by:

$\begin{aligned} A & = \dfrac {\pi}{2} [(r_1+r_2+r_3)^2-r_1^2-r_2^2-r_3^2] \\ & = \dfrac {\pi r_1^2}{2}[(1+2+4)^2-1^2-2^2-4^2] \\ & = \frac {11}{7} \times (\frac {3}{\sqrt{8}})^2 [ 49-1-4-16] \\ & = \frac {11}{7} \times \frac {9}{8} \times 28 \\ & = \frac {99}{2} \\ & = \boxed{49.5} \end{aligned}$

Write a solution. If we draw a line EG further to meet the line AD out of the circle at, say, point H. And let the centers are O1, O2, O3 for small, medium, and big circles respectively. When we draw the radii towards the tangents, all angles are 90 degrees, and we'll see that there are 3 triangles: HGO1, HFO2, & HEO3.

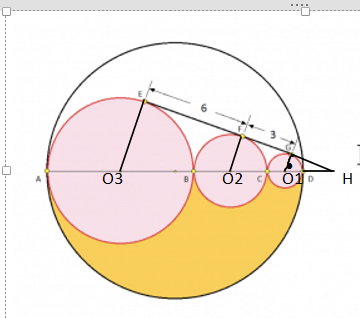
These three share the same H angle and are all right-angled triangles, so they are similar. Then suppose r is the radius of small circle; and R is the radius of the medium circle. The ratio of EF:FG=O3E:O2F=6/3=2, so the big circle has a radius of 2R. Then O2O3:O2O1= 2R+R:R+r = 2, so 3R=2R+2r, or R=2r. The radius of the medium is 2r and that of big circle is 4r.

Now, considering triangles HEO3 and HFO2, 6+3+GH = 2(3+GH) as the ratio is again 2, and GH is 3 and HO1 is 3r.

The small triangle HGO1 is right-angled, so (3r)^2 = r^2+3^2; r^2= 9/8.

The rest is simple; the gold region area= pi/2((7r)^2-(4r)^2-(2r)^2-r^2) = 14pi (r^2)= 14pi (9/8)= (63/4)pi, which will be approximately 49.48.

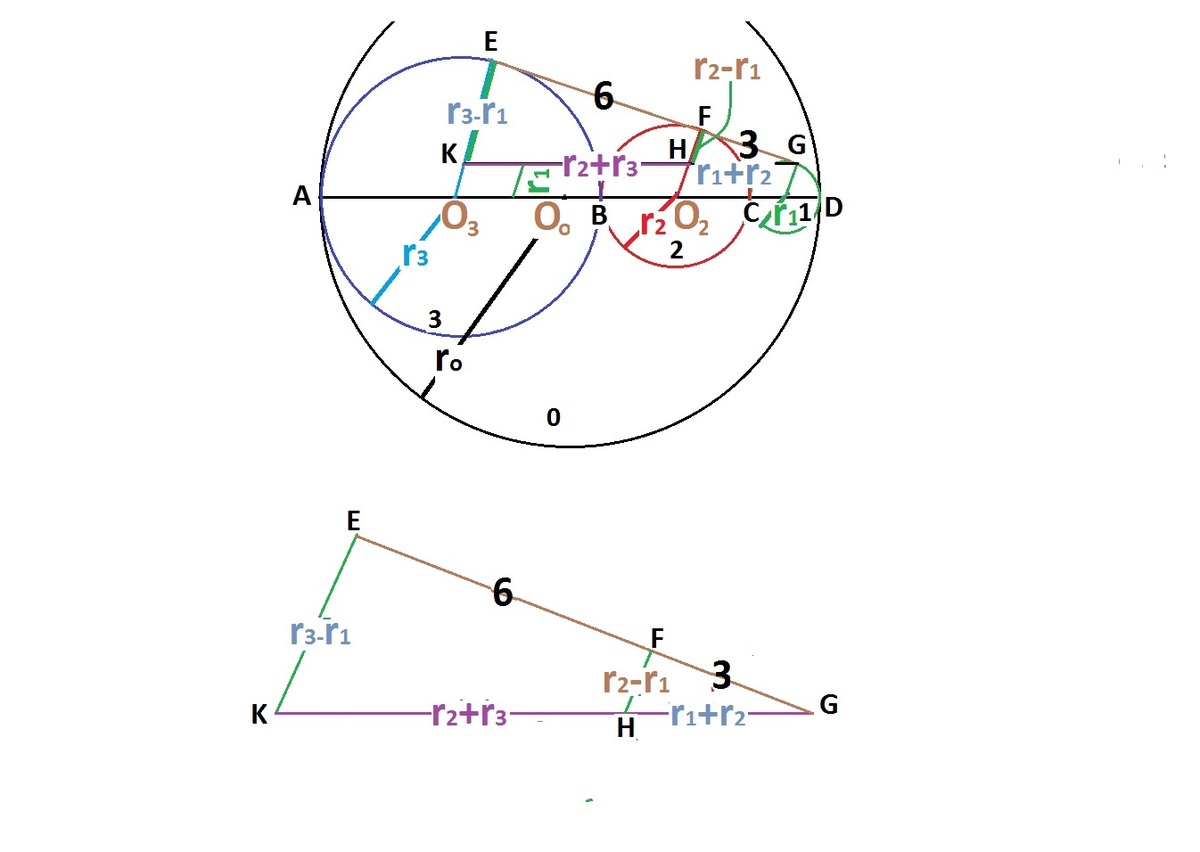
$O_0,~ O_1,~ O_2,~ O_3~are~the~centres~of~Biggest,~Smallest,~Small,~and ~\\~Big~circles~respectively. ~GK \parallel AD~cut~ FO_2 ~at~H~and~EO_3~ at~K.\\In~\triangle EGK,~FH ~ \parallel EK~\implies~the~following~ratios.\\ GH=r_1+r_2…HK=r_2+r_3...FH=r_2-r_1...EK=r_3-r_1\\ \dfrac{r_1 + r_2}{3}=\dfrac{r_2+r_3}{6}~~~and~~ \dfrac{r_2-r_1}{3}=\dfrac{r_3-r_1}{9}\\ Solving~for~r_1:- \\~r_2=2r_1,…r_3=4r_1 \implies r_0=r_1+r_2+r_3=7r_1\\ In~rt.\angle ~ \triangle GFH~ rt ~\angle~at~ F\\GH^2-FH^2=3^2\implies (r_1+r_2)^2 -( r_2-r_1)^2=8*r_1^2=9…. r_1^2=\dfrac{9}{8} \\Requiered~ area~ \\=\dfrac{\pi}{2}*\{r_0^2- r_0^1- r_2^2- r_3^2\}\\=\dfrac{\pi}{2}*\{7^2- 1^1- 2^2- 4^2\}*r_1^2 \\=\dfrac{\pi}{2}*28*\dfrac{9}{8}~~~~~~~=\boxed{\color{#D61F06}{49.5} }$ .