What A Weird Shape!
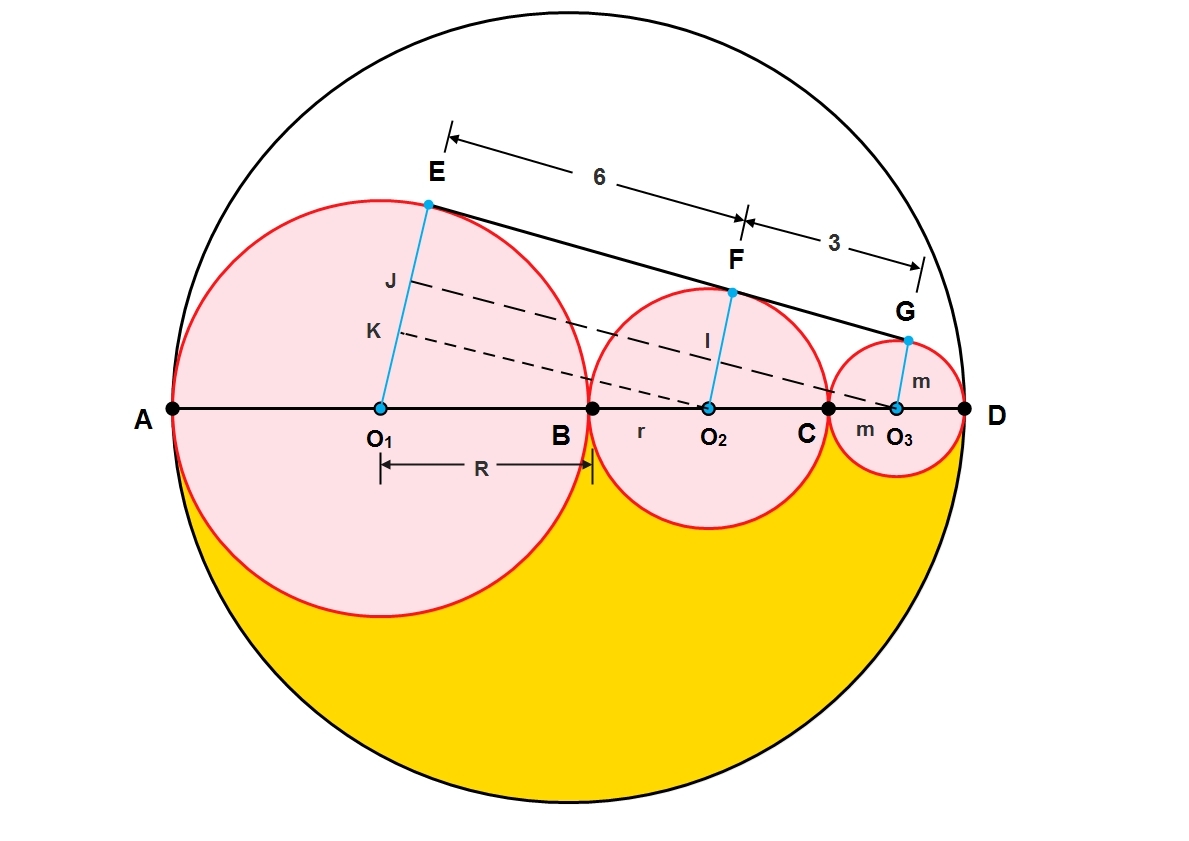
There is a common tangent which intersects the three tangent circles shown above at E , F , and G . If E F = 6 and F G = 3 , find the area of the orange region. Use the approximation π ≈ 7 2 2 .
The answer is 49.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Discussions for this problem are now closed

Really nice solution , no need to actually find radius.Good
Well , I found out the radius. :P
I also calculated the radius.
@Gautam Sharma – Let S = 4 π × ( a 2 + b 2 + a × b )
Put a = 6 , b = 3. find S.
 Imgur
Imgur
We can consider this region as two 'nested' Arbeloses!
So after finding a b = 9 ; b c = 4 9 ; a c = 2 9 [I did not show working here as most solutions in the thread have already done it]
Area of the green Arbelos = π a b = 9 π . . . . see this video for what is an Arbelos and the interesting expression for its area.
Area of yellow Arbelos = π c ( a + b ) = π c a + π c b = π ( 2 9 + 4 9 )
Add the two for total area A = 7 2 2 × 9 ( 1 + 2 1 + 4 1 ) = 4 9 . 5
For another interesting property of an Arbelos see this note
Thanks. Very nice and interesting. Where do you get all this from?
Thank you Sir! Don't remember now, but was probably doing a video on geometric construction to find square roots when I came across this shape. There are a many others with interesting properties like special areas, perimeters . . . all discovered by the ancient geometers! May be creating notes on these would be useful.
Please do create notes.
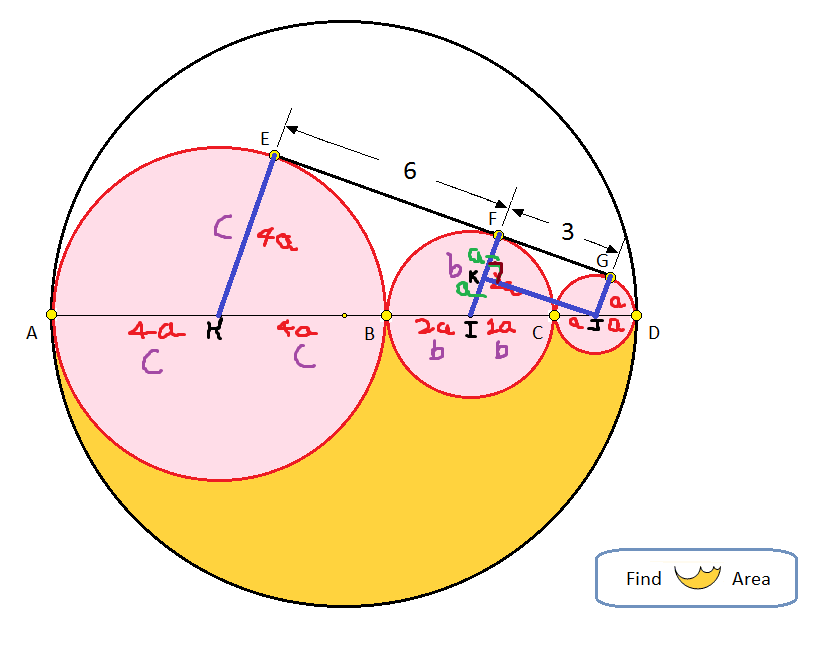
Let the radii of the circles be a , b , c
We know , b = a c … ( 1 )
Also , similarity gives us -
F E G F = I H J I ⇒ 6 3 = b + c ) a + b ⇒ 6 3 = b + c ) a + b
This relation gives us 2 a + b = c . . . ( 2 )
Also , [ G J H E ] = [ G J I F ] + [ F I H E ]
⇒ 2 1 ( a + c ) ( 9 ) = 2 1 ( a + b ) ( 3 ) + 2 1 ( b + c ) ( 6 )
After simplifying this , we get c = 3 b − 2 a . . . ( 3 )
Equating ( 2 ) , ( 3 )
2 a + b = 3 b − 2 a ⇒ b = 2 a
From relation ( 1 ) and b = 2 a , we get , c = 4 a
Also , Area of shaded region = 2 1 × 7 2 2 ( 7 a ) ( 7 a ) − 2 1 × 7 2 2 ( 4 a ) ( 4 a ) − 2 1 × 7 2 2 ( 2 a ) ( 2 a ) − 2 1 × 7 2 2 ( a ) ( a )
= 7 7 a 2 − 7 1 1 ( 1 6 a 2 + 4 a 2 + a 2 )
= 7 7 a 2 − 3 3 a 2
= 4 4 a 2 .
Let J K ⊥ F I giving us Δ J K I , J K = 3 , K I = a , J I = 3 a
Using Pythagoras theorem , 9 a 2 = 3 2 + a 2
8 a 2 = 9
a = 4 3 ( 2 )
So , area of shaded region = 4 4 a 2 = 4 4 ( 4 3 ( 2 ) ) 2 = 4 4 × 1 6 1 8 = 2 9 9 = 4 9 . 5
Using similar logic as Banti Paswan , maybe shorter solution. Let the radii of circles AB, BC and CD be r 3 , r 2 and r 1 respectively. Using Banti's diagram, we notice that:
⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ O 2 O 3 2 − O 2 N 2 = O 3 N ⇒ ( r 2 + r 1 ) 2 − ( r 2 − r 1 ) 2 = 3 2 O 1 O 2 2 − O 1 P 2 = O 2 P ⇒ ( r 3 + r 2 ) 2 − ( r 3 − r 2 ) 2 = 6 2 O 1 O 3 2 − O 1 Q 2 = O 3 Q ⇒ ( r 3 + 2 r 2 + r 1 ) 2 − ( r 3 − r 1 ) 2 = ( 3 + 6 ) 2 ⇒ 4 r 1 r 2 = 9 ⇒ 4 r 2 r 3 = 3 6 = 8 1 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
From Eqn 2 ÷ Eqn 1: ⇒ r 1 r 3 = 4 ⇒ r 3 = 4 r 1 . Substituting this in Eqn 3:
( r 3 + 2 r 2 + r 1 ) 2 − ( r 3 − r 1 ) 2 ( 5 r 1 + 2 r 2 ) 2 − ( 3 r 1 ) 2 1 6 r 1 2 + 2 0 r 1 r 2 + 4 r 2 2 1 6 r 1 2 + 5 ( 4 r 1 r 2 ) + 4 r 2 2 1 6 r 1 2 + 5 ( 9 ) + 4 r 2 2 1 6 r 1 2 + 4 r 2 2 4 r 1 2 + r 2 2 4 r 1 2 + r 2 2 4 r 1 2 − 4 r 1 r 2 + r 2 2 ( 2 r 1 − r 2 ) 2 = 8 1 = 8 1 = 8 1 = 8 1 = 8 1 = 3 6 = 9 = 4 r 1 r 2 = 0 = 0 \
⇒ r 2 = 2 r 1 ⇒ 8 r 1 2 = 9 ⇒ r 1 = 8 3 ⇒ r 2 = 8 6 ⇒ r 3 = 8 1 2
The area of the orange shaded region is given by:
A = 2 π [ ( r 1 + r 2 + r 3 ) 2 − r 1 2 − r 2 2 − r 3 2 ] = 2 π r 1 2 [ ( 1 + 2 + 4 ) 2 − 1 2 − 2 2 − 4 2 ] = 7 1 1 × ( 8 3 ) 2 [ 4 9 − 1 − 4 − 1 6 ] = 7 1 1 × 8 9 × 2 8 = 2 9 9 = 4 9 . 5
Your and @Banti Paswan 's solution needs advance geometry , while @Nihar Mahajan 's solution is just simple pure geometry. But I like both!
Write a solution. If we draw a line EG further to meet the line AD out of the circle at, say, point H. And let the centers are O1, O2, O3 for small, medium, and big circles respectively. When we draw the radii towards the tangents, all angles are 90 degrees, and we'll see that there are 3 triangles: HGO1, HFO2, & HEO3.
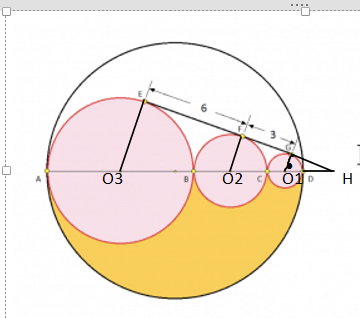
These three share the same H angle and are all right-angled triangles, so they are similar. Then suppose r is the radius of small circle; and R is the radius of the medium circle. The ratio of EF:FG=O3E:O2F=6/3=2, so the big circle has a radius of 2R. Then O2O3:O2O1= 2R+R:R+r = 2, so 3R=2R+2r, or R=2r. The radius of the medium is 2r and that of big circle is 4r.
Now, considering triangles HEO3 and HFO2, 6+3+GH = 2(3+GH) as the ratio is again 2, and GH is 3 and HO1 is 3r.
The small triangle HGO1 is right-angled, so (3r)^2 = r^2+3^2; r^2= 9/8.
The rest is simple; the gold region area= pi/2((7r)^2-(4r)^2-(2r)^2-r^2) = 14pi (r^2)= 14pi (9/8)= (63/4)pi, which will be approximately 49.48.
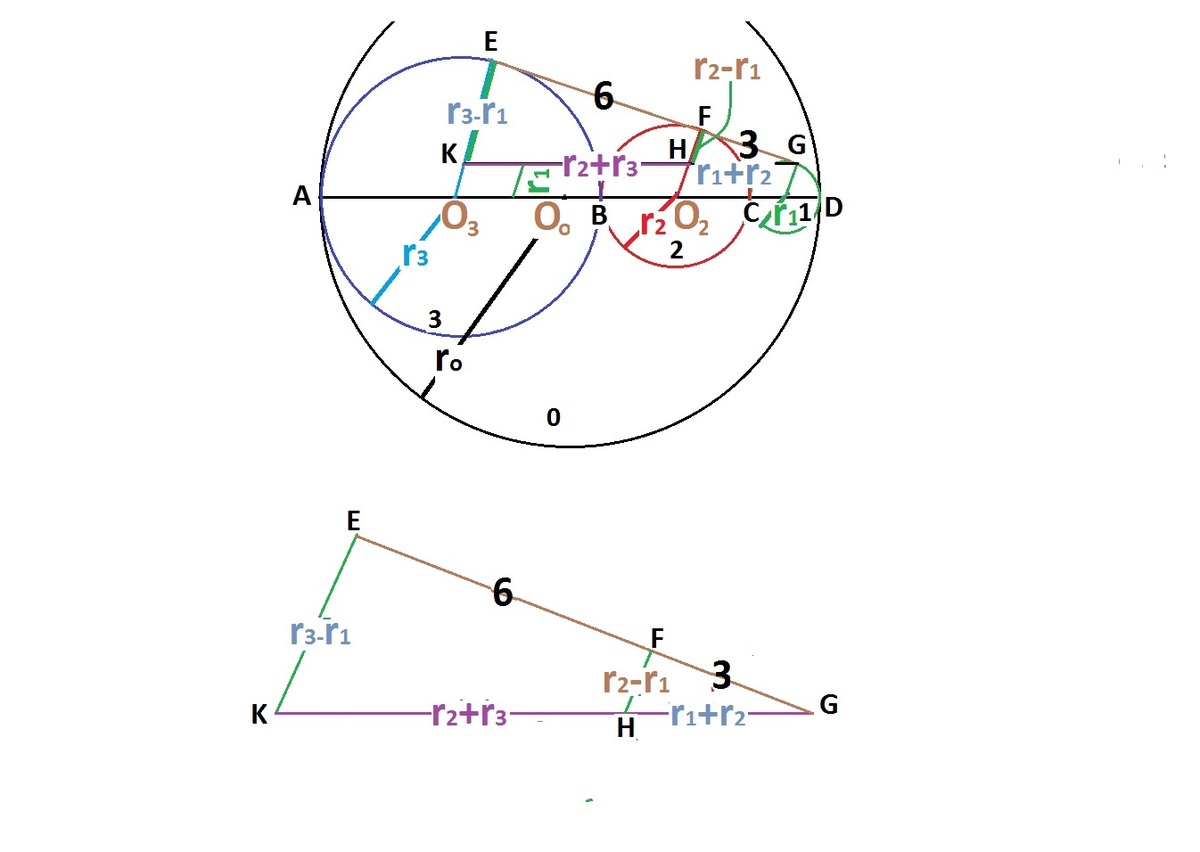
O
0
,
O
1
,
O
2
,
O
3
a
r
e
t
h
e
c
e
n
t
r
e
s
o
f
B
i
g
g
e
s
t
,
S
m
a
l
l
e
s
t
,
S
m
a
l
l
,
a
n
d
B
i
g
c
i
r
c
l
e
s
r
e
s
p
e
c
t
i
v
e
l
y
.
G
K
∥
A
D
c
u
t
F
O
2
a
t
H
a
n
d
E
O
3
a
t
K
.
I
n
△
E
G
K
,
F
H
∥
E
K
⟹
t
h
e
f
o
l
l
o
w
i
n
g
r
a
t
i
o
s
.
G
H
=
r
1
+
r
2
…
H
K
=
r
2
+
r
3
.
.
.
F
H
=
r
2
−
r
1
.
.
.
E
K
=
r
3
−
r
1
3
r
1
+
r
2
=
6
r
2
+
r
3
a
n
d
3
r
2
−
r
1
=
9
r
3
−
r
1
S
o
l
v
i
n
g
f
o
r
r
1
:
−
r
2
=
2
r
1
,
…
r
3
=
4
r
1
⟹
r
0
=
r
1
+
r
2
+
r
3
=
7
r
1
I
n
r
t
.
∠
△
G
F
H
r
t
∠
a
t
F
G
H
2
−
F
H
2
=
3
2
⟹
(
r
1
+
r
2
)
2
−
(
r
2
−
r
1
)
2
=
8
∗
r
1
2
=
9
…
.
r
1
2
=
8
9
R
e
q
u
i
e
r
e
d
a
r
e
a
=
2
π
∗
{
r
0
2
−
r
0
1
−
r
2
2
−
r
3
2
}
=
2
π
∗
{
7
2
−
1
1
−
2
2
−
4
2
}
∗
r
1
2
=
2
π
∗
2
8
∗
8
9
=
4
9
.
5
.