Climbing a staircase

Algebra Level 3

Let $F(x)$ be a non-decreasing function defined on $[0, 1 ]$ such that

$\begin{cases} 2 F \left ( \frac{x}{3} \right) = F(x), \\ F(x) + F(1-x) = 1 .\\ \end{cases}$

What is the value of $F ( \frac{1}{13} )$ ?

\frac{1}{13}

\frac{1}{8}

\frac{2}{13}

\frac{1}{7}

3 solutions

Sudeep Salgia
Mar 19, 2015

Finding the value of $F\left(\dfrac{1}{13}\right)$ just requires a clever manipulation as follows.

$\displaystyle F\left(\frac{1}{13}\right) + F\left(\frac{12}{13}\right) = 1$

$\displaystyle \begin{array}{c}\\ F\left(\frac{12}{13}\right)&& = 2 F\left(\frac{4}{13}\right) \\ && = 2 \left( 1 - F\left(\frac{9}{13}\right) \right) \\ && = 2 - 2 F\left(\frac{9}{13}\right) \\ && = 2 - 4 F\left(\frac{3}{13}\right) \\ && = 2- 8 F\left(\frac{1}{13}\right) \\ \end{array}$

$\displaystyle \Rightarrow 1 - F\left(\frac{1}{13}\right) = 2 - 8 F\left(\frac{1}{13}\right)$

$\displaystyle \therefore F\left(\frac{1}{13}\right) = \frac{1}{7}$

Any idea how to solve the general case?

Hint: What condition have you not used yet?

Calvin Lin Staff - 6 years, 2 months ago

Really clever solution!

Sanjeet Raria - 6 years, 2 months ago

It seems that you do not even use the condition that f(x) is a non-decreasing function?

沂泓纪 - 5 years, 2 months ago

That information is needed to solve the general case, like finding the value of $f ( \frac{1}{\pi} )$ .

See Ivan's solution for the description of the general solution.

Calvin Lin Staff - 5 years, 2 months ago

Ivan Koswara
Mar 20, 2015

This is also known as the Cantor function or the Devil's staircase (which gives the name of the problem). An alternate method to find $F(x)$ is as follows:

Express $x$ in base 3.
If it contains a $1$ , remove everything after the first $1$ encountered.
Replace all $2$ with $1$ .
Read the number in base 2.

For $\frac{1}{13} = 0.002002002\ldots _3$ , this gives $0.001001001\ldots _2 = \boxed{\frac{1}{7}}$ .

Yes, that's the functional solution. Do you know how to prove it?

Calvin Lin Staff - 6 years, 2 months ago

I'd like to attempt to prove it !

Are there any "tough to be found" intermediate results required to do the task ?

Thanks

Arousse Fares - 2 years, 8 months ago

No, this is considered a "standard" functional equations problem in the olympiad.

Hint: That the function is non-decreasing hasn't been used in Sudeep's solution to find $f(\frac{1}{13} )$ . Thus, most likely, it is used when defining the function on all real numbers. This suggests that we just need to define the function on a dense subset of $[0,1]$ .

Calvin Lin Staff - 2 years, 8 months ago

@Calvin Lin – Done. I'm sorry for being a little bit late. I got lazy in the middle ^^... As an apology, I've found a different way to express $F(x)$ than the one given by Ivan. Also, although I have to recheck my notes, I think I've made another problem by solving this one !

And, just to make sure, would you mind checking this argument ? :

(A) : if we show that there is, at most, only one mapping, then there is, at most, only one functional solution.

(B) : If we find a functional solution and (A) is true, we've found all functional solutions.

Arousse Fares - 2 years, 7 months ago

@Arousse Fares – A) What is the difference between "mapping" and "functional solution"? To me they mean the same thing, so if you can clarify the word "mapping", that would be helpful.

B) For this functional equation, I've not seen a solution whose main thrust is "there exists a unique solution to this functional equation. We found one that works, hence it is the only one.
Note: It is true that there is a unique solution to this functional equation, but that arises out of the work done.

Calvin Lin Staff - 2 years, 7 months ago

@Calvin Lin – After thinking it through, It is redundant... But never mind that. Here is the proof :

So it will be done in two steps. The first is to find a functional solution satisfying all the conditions and the second will be to show that there is only one possible functional solution.

Step 1 (the solution) :

Represent the interval $\left [ 0 ; 1 \right ]$ as a segment.
Divide it into three equal parts, take the middle one and color it.
Repeat (2) with the non colored segments again and again $n$ times. $n$ being the number of times it will take to reach $x$ . Here is an example with n = 1 , 2 and 3 :

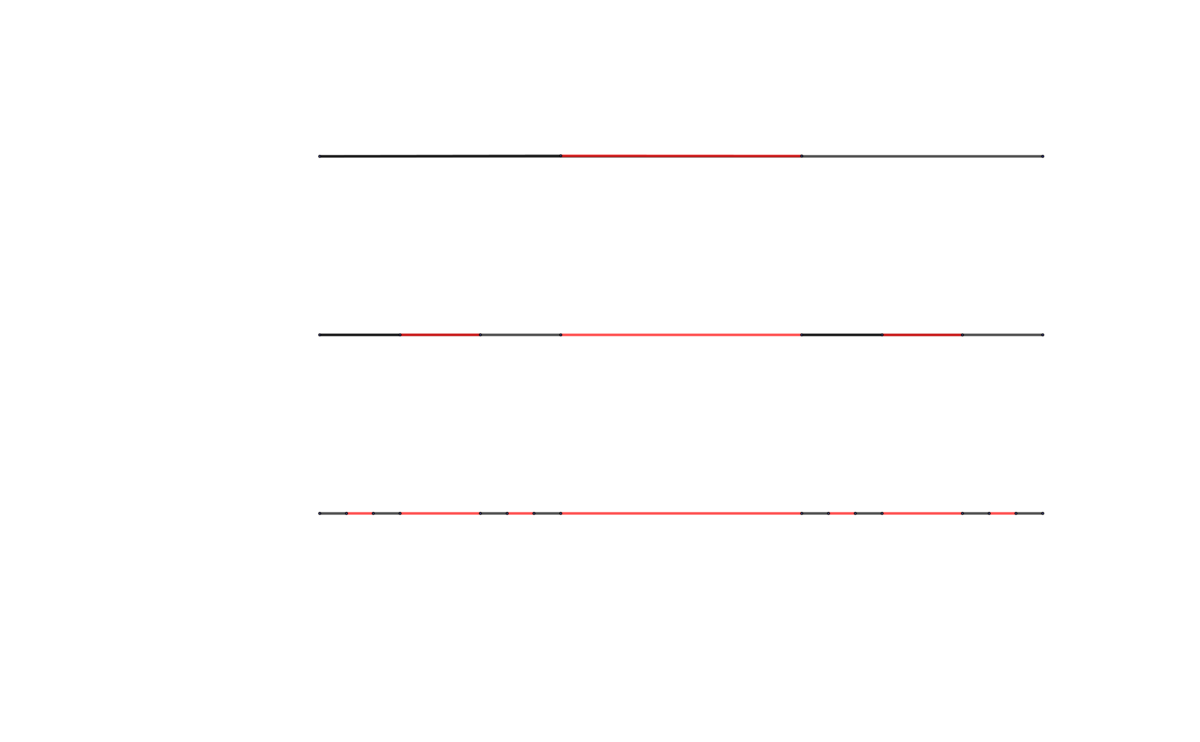
4 Now, from left to right, assign to each colored interval the value $\frac{k}{2^{n}}$ , $k$ being the interval's ordinal number.

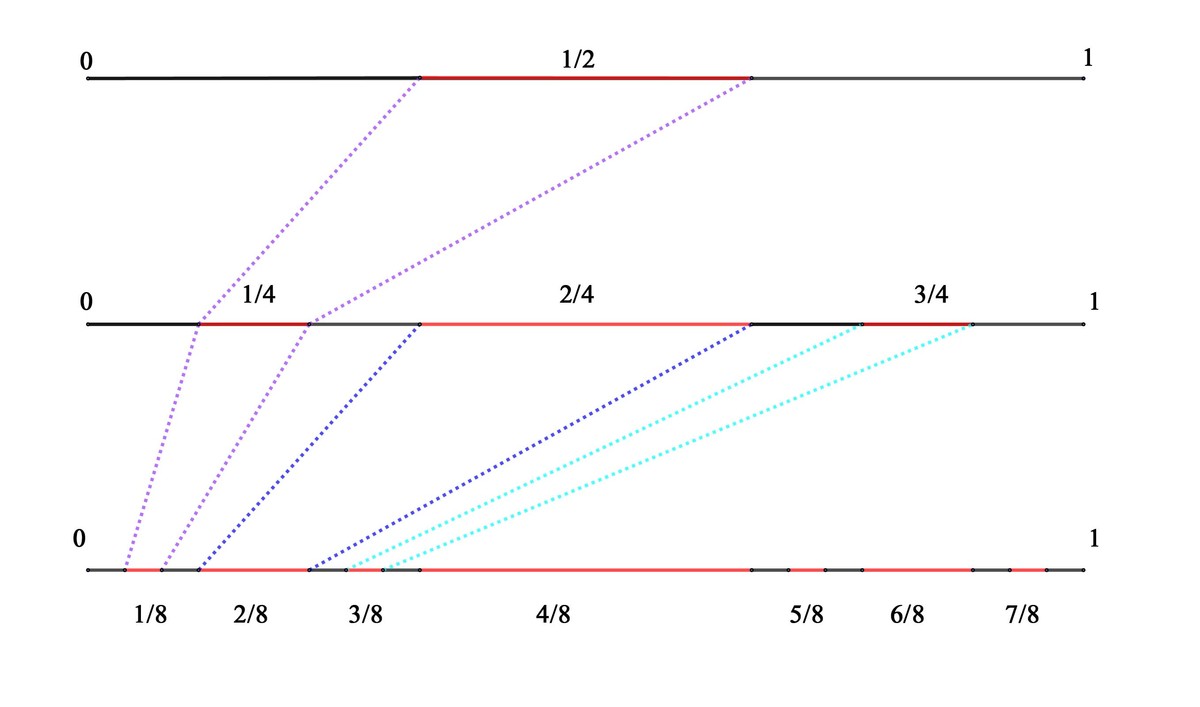
Now we need to prove that this function satisfies all the required conditions. The only one (condition) that may stir some trouble is that $2F(\frac{x}{3}) = F(x)$ . To show that it is true for the functional solution, we can use iteration. A graph is also very helpful here :

Step 2 (That there is only one solution) :

The idea is that there are two actions we can do on $F(x)$ . Namely : $F(x) = 1 - F(1-x)$ and $F(x) = 2F(\frac{x}{3})$ . If it is true that $F(x)$ can be expressed in terms of $F(y)$ such as $y \in [ \frac{1}{3} ; \frac{2}{3} ]$ then, since $F(y) = \frac{1}{2}$ , it means there is only one way to define $F(x)$ since it's a first degree equation. I have failed to express it with algebra so I'll be using another graph ^^ :

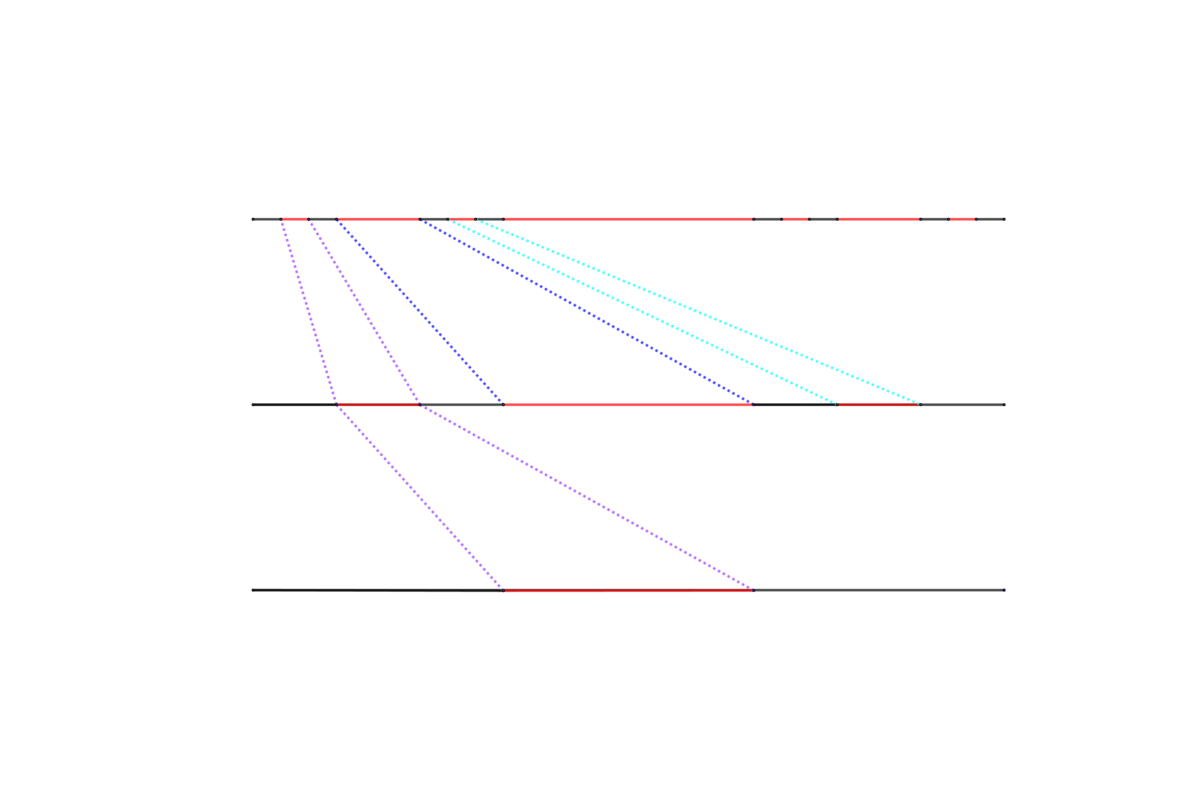
It's pretty much the same as the previous one if not that this one is backwards. Meaning that the iteration should be done starting from $x$ . And since we are allowed to express $x$ in terms of $1-x$ , there should be no problem.

Arousse Fares - 2 years, 7 months ago

@Arousse Fares – Once again, I disagree with

So it will be done in two steps. The first is to find a functional solution satisfying all the conditions and the second will be to show that there is only one possible functional solution.

and you have not shown that in your solution. It seems to me the main reason you didn't discover this misconception is because you only considered rational values, and not irrational values.

The gaps that you have are

In step 1, did not show that $F(x)$ exists for all $x$ . The "assign to each colored interval the value $\frac{k}{2^n}$ " is somewhat meaningless, and possibly you had some idea that wasn't written down. My best guess of what you mean for "interval $[ \frac{1}{3}, \frac{2}{3} ]$ is assigned the value $\frac{1}{2}$ " is that if $y \in [ \frac{1}{3}, \frac{2}{3} ]$ , then $f(y) = \frac{1}{2}$ . Note that endpoints need to be carefullly treated.
It seems like you want some kind of limiting process, but have yet to show that the limiting process converges. In particular, how would we find $F( \frac{1}{\sqrt{2} } )$ ?
In step 2, that has nothing to do with showing the uniqueness of a solution. Typically, such an approach is to assume that 2 solutions exists, and then we want to show that $F_1 (x) = F_2(x)$ . In particular, how do we show that $F_1 ( \frac{1}{\sqrt{2} } ) = F_2 ( \frac{1}{\sqrt{2} } )$ ?
Note that you did not use the "non-decreasing" condition, so that suggests the possibility that your solution is incomplete, or that additional information was provided which was not necessary. In this case, to calculate $F( \frac{1}{\sqrt{2} } )$ , we do have to use the "non-decreasing" condition.

If $x= \frac{n}{m}$ is a rational number, then we can determine $F(x)$ by considering the values of $F( \frac{ \cdot } { m } )$ in a similar manner to the "algebraic manipulation" steps shown in the solutions. However, if $x$ is an irrational number, then simply looking at $x \rightarrow 2x, \frac{x}{2}, 1 - x$ would not be sufficient for us, because each time we introduce a new variable into the system of equations.

The above comment should give you some sense of how this "standard Olympiad functional equation" problem is done, namely
1. Determine a closed form for value of $F(x)$ when $x$ is rational (as described by Ivan above). Show that this value is uniquely determined.
2. Use the non-decreasing property to determine that the same formula holds for the irrational numbers. Show that the value is uniquely determined since the rational numbers are dense.

Calvin Lin Staff - 2 years, 7 months ago

@Calvin Lin – Sorry if it's a bother but I'd like to make the corrections one by one ^^.

(1&2). "did not show that $F(x)$ exists for all $x$ "

Let us consider this sequence : $\left \{ \left [ \frac{1}{3},\frac{2}{3} \right ],\left [ \frac{1}{9},\frac{2}{9} \right ]\cup \left [ \frac{3}{9},\frac{6}{9} \right ] \cup \left [ \frac{7}{9},\frac{8}{9} \right ], ... \right \}$

Doesn't it converge to $\left [ 0,1 \right ]$ ? And isn't the "functional solution" producing this exact sequence ?

" The "assign to each colored interval the value $\frac{k}{2^{n}}$ is somewhat meaningless[...] "

To rewrite it in terms of the sequence : For every $x$ that belongs to the $k^{th}$ interval of the $n^{th}$ element of the sequence, $F(x) = \frac{k}{2^{n}}$ . Example : $\frac{1}{ \sqrt{2} } \in \left [ \frac{19}{27},\frac{20}{27} \right ]$ which is the fifth interval of the third element of the sequence. Therefore $F(\frac{1}{\sqrt{2}}) = \frac{5}{2^3}$

Any problem up to this point ?

Arousse Fares - 2 years, 7 months ago

@Arousse Fares – My point is precisely that your comment is lacking those details, which remains to be shown. I knew that you were missing some points, but didn't know which ones. Admittedly $\frac{1}{ \sqrt{2} }$ wasn't a valid counterexample.

Now that I understand what you wanted to do, and after reading through your solution in more detail, I see that one way to "describe" your sets at the $n$ th step is that "the Trenary decimal expansion contains a 1". In particular, the following numbers will not lie in any of the intervals you listed.

$0$ (even though we can calculate that $f(0) = 0$ .)
The rational number $\frac{3}{4}$ (even though we can calculate that $f (\frac{3}{4} ) = \frac{2}{3}$ .)
The irrational number $0.20200200020000\ldots_3$ (which I claim we cannot calculate using only the formulas)

So, how does your process give us the value of either of these 3 numbers?

Note: What do you mean by "converge to $[ 0, 1 ]$ "? There is no mathematical definition for converge to an interval, so I do (definitively) know what you mean.

If your claim is that "The union of all of these sets (which are contained within each other) is $[ 0,1]$ ", then that claim is not true. In fact, $[ 0,1]$ cannot be expressed as the countable disjoint union of at least 2 closed sets , and we're missing out uncountably many points.

If your claim is that "the closure of the union of these sets is $[ 0,1 ]$ ", then that claim is true. However, simply being the closure doesn't yet yield a unique value. We still have to use the fact that the function is non-decreasing. However, your comment didn't indicate an awareness of this aspect.

To be fair, these facts requires more extensive knowledge, and I otherwise understand why you would be tempted to say "These intervals converge to $[ 0,1]$ ".

Note: I use "describe" because there needs to be some clarification about the right endpoint of your intervals. Even though $\frac{2}{3} = 0.2_3$ doesn't fit "trenary expansion contains a 1", I'm essentially using $\frac{2}{3} = 0.12222\ldots _3$ which contains a 1.

A complete description of the numbers that you're missing out are the uncountably many whose ternary expansion doesn't contain a 1, excluding the countably many whose ternary expansion has an ending string of "all 2's".

Note: I do not know what you mean by "And isn't the "functional solution" producing this exact sequence ?".
What do you refer to by "functional solution"? Are you talking about your approach of algorithmically defining the solution? Or are you referring to "solution to the functional equation"?

Calvin Lin Staff - 2 years, 7 months ago

@Calvin Lin – So I think I understand the issues.

I had two misconceptions :

That any $x$ could be reached by the algorithm. Your counterexamples are the refutation to it. I also found that $F(\frac{2}{3^{n}-1})=\frac{1}{2^{n}-1}$ so the algo indeed does have quite a bunch of holes...
That doing the algorithm infinitely many times would end up covering the entirety of $[0,1]$ . (thus the use of the term convergence...).

As for when I said "functional solution", it meant the algorithm. I put the guillemets in there because its position as a functional solution was questioned...

I'll try to add elements to the algorithm to make it work for all of $[0,1]$ . If you say it's too difficult a task, I'll just switch to the method you gave on the previous comment.

Arousse Fares - 2 years, 7 months ago

@Arousse Fares – This is how I would write up your approach.

Show that on those intervals, the values are uniquely determined. (Use the formulas + non-decreasing)
Let the (infinite) union of those intervals be $A$ . Show that the closure of $A$ is $[ 0,1 ]$ .
Define $f: A \rightarrow \mathbb{R}$ using the assigned values. and show that $f$ satisfies the conditions. (There is a slight distinction between step 1's " $f(x)$ is uniquely determined", and step 3's "there is no possible contradiction with any condition by setting $f(x)$ in this manner".)
Show that for any real $x \in [ 0,1 ]$ , for any sequence $a _i \in A$ , then $f(a_i)$ converges to the same value. Hence, because the function is non-decreasing + the closure of $A$ is $[0,1]$ , hence if we could extend the domain of the function from $A$ to $[0,1]$ , then this is the unique value that is allowed. Define $g: [0,1] \rightarrow \mathbb{R}$ to be this unique value. (I'm mainly refraining from using $f(x)$ to avoid abuse of notation.) There is some non-trivial work here with limits, esp $\delta, \epsilon$ tracking. Non-decreasing will need to be used here.
Show that $g(x)$ satisfies the conditions in the question. (The difference from step 4 and 5 is the difference between steps 1 and 3 for the set $A$ .) Again, there is some non-trivial work here, and you're interchanging sequence of limits, so have to be careful for when that is allowed.
Conclude that this function works.
As a corollary, the function is unique because each value is uniquely determined (This defers from your attempt to directly prove that the function is unique).

Calvin Lin Staff - 2 years, 7 months ago

@Calvin Lin – I'll borrow your notation :

Let $x \in [\frac{1}{3},\frac{2}{3}]$ . Then $F(x)=\frac{1}{2}$ Then, all the elements of this sequence : $\{F(\frac{x}{3}) , F(1-\frac{x}{3}) , F(\frac{x}{9}) , F(1-\frac{x}{9}) , F(\frac{1- \frac{x}{3}}{3}), ...\}$ are all uniquely determined. Therefore $f(x)$ 's intervals are all uniquely determined.
Consider the metric space $([0,1],d)$ , $d(x,y)$ being the standard Euclidean distance between 2 points. We know that $A$ is a subset of $[0,1]$ . If the length of $A$ : $l(A)$ equals 1, then the closure of $A$ is $[0,1]$ .

$l(A) = \sum_{k=1}^{\infty} \frac{2^{k-1}}{3^{k}} = \frac{1}{3}(1+2l(A))$ . Therefore $l(A)=1$ . Therefore the closure of $A$ is $[0,1]$ .

Can I continue ?

Arousse Fares - 2 years, 7 months ago

@Arousse Fares – For step 1, I meant something different. Namely you said that the value on the $k$ th interval at step $n$ is equal to $\frac{k}{2^n}$ . My question is "Does this value every change? How do we know it is a constant?".

And yes, I know that the answer is "No, the value doesn't change. It is a constant", but this needs to be made explicit.

Calvin Lin Staff - 2 years, 7 months ago

@Calvin Lin – Would it be enough to show that the $k$ th interval at step $n$ (to which is assigned the value $\frac{k}{2^{n}}$ ) is the $2k$ th interval at step $n+1$ (to which would be assigned the value $\frac{2k}{2^{n+1}}$ ) ? But it doesn't require to use the formulas nor the non-decreasing property so I'm quite confused here...

Arousse Fares - 2 years, 7 months ago

@Arousse Fares – That's partly my fault. The point of step 1 is to ensure that the values you defined for the function on the interval is well-defined. You are right to say that it doesn't need any properties in order for us to ensure that the function is well-defined.

However, I was then trying to motivate why we would want to set those values in step 1 (IE how do we explain the magic that makes this work). If so, the values in step 1 are determined by the formulas+non-decreasing.

Calvin Lin Staff - 2 years, 7 months ago

@Calvin Lin – There is some confusion between "step 1" of the proof and "step 1" of the algorithm... When speaking of the proof's steps, from here on, I'll be using S1,S2 , ... S7.

Returning to the proof : S1 can be done recursively quite easily with the argument used in my previous comment (but I don't mind doing it rigorously If you insist on it). I'll also assume there is no (big?) issue with the argument for S2 so can I move on to S3 ?

Arousse Fares - 2 years, 7 months ago

@Arousse Fares – S1 - RIght, if we're just focused on defining the values on this intervals, then this step is pretty direct.

S2 - Yea, this is almost obvious. As a side note, the way to prove this rigorously is that if we want to get $\epsilon < (\frac{2}{3})^n$ close to a point $x$ , then we are guaranteed such a value in an interval at step $n$ . This allows us to create a sequence of $x_n$ which approximate $x$ .

Calvin Lin Staff - 2 years, 7 months ago

@Calvin Lin – S3:

Let $B:=\{x,1-x, \frac{x}{3} , 1-\frac{x}{3} , \frac{x}{9} , 1-\frac{x}{9} , \frac{1- \frac{x}{3}}{3}, ... \forall x \in [\frac{1}{3},\frac{2}{3}] \}$ . Then $f(b) = \frac{k}{2^{n}} \forall b \in B$ . $k$ and $n$ being the $k$ th interval that has $b$ of the $n$ th element of this sequence $\left \{ \left [ \frac{1}{3},\frac{2}{3} \right ],\left [ \frac{1}{9},\frac{2}{9} \right ]\cup \left [ \frac{3}{9},\frac{6}{9} \right ] \cup \left [ \frac{7}{9},\frac{8}{9} \right ], ... \right \}$

But since this is just a (fancy) way of saying that : to the kth interval of the nth element of the sequence, assign a value $\frac{k}{2^{n}}$ , it's also straightforward to show that $f$ abides to the conditions (namely, that the formulas work for it (formula 1 : noticing that $F(x)=\frac{1}{2}\forall x \in [\frac{1}{3},\frac{2}{3}]$ then recurrence. formula 2 : basic algebra) and that it's non decreasing(...).). I think it makes more sense to deal with n=1 here than in S1 as it's by showing that $f$ is coherent with the formulas that the mystery behind the trick vanishes... S4 ?

Arousse Fares - 2 years, 7 months ago

@Arousse Fares – S3 - No, what you have done here is S1, where we defined the value on each interval. Your working shows that these values are uniquely defined on $A$ , IF the function exists.

The point of S3 is to show that these values are also the conditions in the problem hold on set A, or that the function indeed exists on the restricted domain $A$ .

IE For a given $x \in A$ , prove that $2 F ( \frac{x}{3} ) = F(x)$ and $F(x) + F(1-x) = 1$ . Of course, this assumes that $\frac{x}{3}, 1 - x \in A$ (which should be shown).

This distinction was mentioned above:

(There is a slight distinction between step 1's " $f(x)$ is uniquely determined", and step 3's "there is no possible contradiction with any condition by setting $f(x)$ in this manner".)

Calvin Lin Staff - 2 years, 7 months ago

Nathan Couch
Mar 20, 2015

I'll admit that I solved it by exploiting the format of the question:

Since $F(1)=1$ , the first condition gives us:

$F(\frac{1}{3})=\frac{1}{2}$
$F(\frac{1}{9})=\frac{1}{4}$
$F(\frac{1}{27})=\frac{1}{8}$

We also know that the function is non-decreasing, so

$F(\frac{1}{9}) \leq F(\frac{1}{13}) \leq F(\frac{1}{27})$

$\frac{1}{4} \leq F(\frac{1}{13}) \leq \frac{1}{8}$

The only answer that meets these criteria is $\frac{1}{7}$ . (edit: this is clearly not true)

Observe that F(1) =1, F(0)=0. Therefore, we'd get F(1/3^n)=1/(2^n).

Method 1: Now we take n=log13(base 3) to get F(1/13) = 1/(2^log13(base 3)) ≈1/(2^2.334717519)=1/7. Method 2: Now, F(1/13) + F(12/13) = 1, which implies that upon extreme simplification, we get 1 - F(1/13) = 2 - 8*F(1/13) which implies F(1/13)=1. Method 3: Check on WolframAlpha.

Alex Fullbuster - 2 years, 1 month ago

Whoops I guess I got lucky when I forgot about $\frac{1}{8}$ . That said, I probably had no business tackling this question anyways.

Nathan Couch - 6 years, 2 months ago

Haha, it takes a bit of work to nail down the exact value of this function. $\frac{2}{13}$ is also in this range that you described.

Calvin Lin Staff - 6 years, 2 months ago

Climbing a staircase

3 solutions

0 pending reports