Closing $f^n$

Since $\cos3u = 4\cos^3u - 3\cos u$ , we note that $f(2\cos u) = 2\cos3u$ , and hence $f^n(2\cos u) \; = \; 2\cos(3^nu)$ Differentiating this identity, we see that $-2\sin u (f^n)'(2\cos u) \; = \;-2\sin(3^nu) \times 3^{n}$ The first identity shoes that $f^n\big(2\cos\tfrac{2k\pi}{3^n}\big) \; = \; 2 \hspace{2cm} k = 0,1,2,...,3^{n-1}$ while the second identity shows that $(f^n)'\big(2\cos\tfrac{2k\pi}{3^n}\big) \;=\; 0 \hspace{2cm} k = 1,2,...,3^{n-1}$ and we note that $2\cos\tfrac{2(3^n-k)\pi}{3^n} \; = \; 2\cos\tfrac{2k\pi}{3^n} \hspace{2cm} k = 1,2,...,\tfrac12(3^n-1)$ Thus $f^n-2$ has the simple root $2$ and the repeated roots $2\cos\tfrac{2k\pi}{3^n}$ for $k = 1,2,...,\tfrac12(3^n-1)$ . Since $f^n-2$ is a polynomial of degree $3^n$ and we have found $1 + 2\times\tfrac12(3^n-1) = 3^n$ roots, we have found them all. Thus there are $1 + \tfrac12(3^n-1) = \tfrac12(3^n+1)$ distinct zeros for $f^n-2$ . When $n=16$ we get the answer $\boxed{21523361}$ .

Similarly, $g^n(2\cos u) \; = \; 2\cos\big(\tfrac{u}{2^n}\big)$ .

I would never have come up with the cosine solutions. Here's how I found the number of solutions.

$f(x)=2$ has two solutions, $x=-1$ and $x=2$

$f^{2}(x)=2$ has five solutions, the two solutions to $f(x)=2$ and three more: the solutions to $f(x)=-1$ . Their values are not important but they can be seen on this graph.

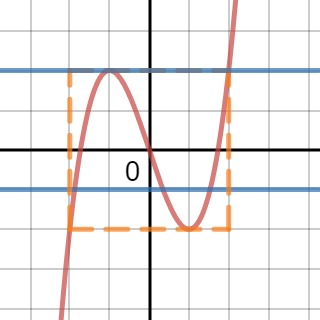
Note the interesting portion of the function is constrained to the orange box. Whenever $-2 \le y \le 2$ , $-2 \le x \le 2$ . This means for each solution to the previous stage there will be 3 values for the next stage with the exception of the solution $x=2$ , it only comes from 2 values.

So the number of solutions almost triples from $n$ to $n+1$ , falling just one short. Call $a_{n}$ the number of solutions to $f^{n}(x)=2$ and we have the recurrence, $a_{1}=2$ , $a_{n+1}=3\cdot a_{n} -1$ for $n>1$ .

I didn't bother finding an explicit formula as this is easy enough to evaluate: $a_{16}=\boxed{21523361}$

let $x = 2 \cos \theta$

1. using identity $\cos 3\theta = 4 \cos^3 \theta - 3 \cos \theta$ , prove that $f(2 \cos \theta) = 2 \cos 3 \theta$

2. the closed form is $f^n(x) = 2 \cos (3^n \arccos (\frac{x}{2}))$

3. prove that :

   a. $x<-2 \implies f(x)<x<-2$

   b. $x>2 \implies f(x)>x>2$

   hence all solutions of $f^n(x) = 2$ lies within $-2 \leq x \leq 2$

4. subs $x = 2 \cos \theta , \ f^n(x) = 2 \implies \cos (3^n \theta) = 1 , \ 0 \leq \theta \leq \pi$

5. by considering the graph of $y = \cos (k \theta)$ , prove that the number of solutions is $\frac{3^n+1}{2}$

(example for $n=2$ )

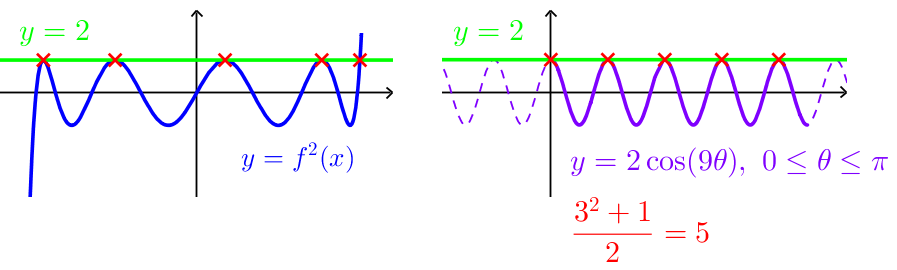
$\therefore \frac{3^{16}+1}{2}=21523361$

Bonus: $g(2 \cos \theta) = \sqrt{2 + 2 \cos \theta} = 2 \cos(\frac{1}{2} \theta) , \ g^n(x) = 2 \cos(2^{-n} \arccos(\frac{x}{2}))$

Note: These 2 are related to Chebyshev polynomials , whose iterated functions have simple closed form.

Let f(1)=x^3-3x, and f(n)=f°f°...f(1), where f is nested n times. We are asked to find number of distinct real zeros of

f(n)-2=0, when n=16,

Let, g(n)=f(n)-2, Thus, we are looking for number of distinct real zeros of

g(n)=0, when n=16,

We show, using Wolfram alpha script "Nest[#^3-3# &,x,n]-2, from n=1,4", that

g(1)=(x-2){(x+1)^2},

{No. of zeros = (1+3^0)}

g(2)=g(1)[{g(1)+3}^2],

g(2)=g(1){(x^3-3x+1)^2},

{No. of zeros=(1+3^0+3^1)}

g(n)=g(n-1)*[{g(n-1)+3}^2],

{No. of Zeros= 1+3^0+3^1+..+3^(n-1)}

Looking at the structure and terms in g(n) for n=1,4, we deduce that number of distinct real zeros of g(n)=0 are given by sum of series

1+3^0+3^1+3^2+....3^(n-1)=(1/2){1+3^n}

which gives for n=16,

Answer=21523361

Warning: This is not a rigorous solution!

The trick with the cosines is the elegant thing to do, but I was way too lazy to think through it. Here is a relatively simple way to guess the solution. I plotted the graphs of $f(x)$ , $f(f(x))$ and $f^3(x)$ :

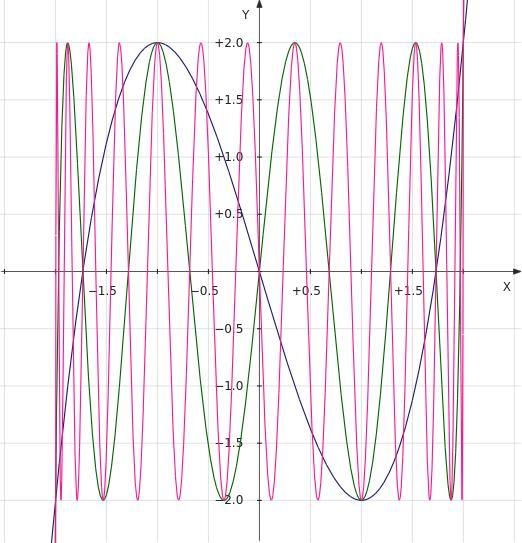
You notice pretty quickly that the roots of $f^n(x)$ are all real, and when look at $f^n(x) -2$ then all the roots but one become double roots. Since you know the degree of $f^n(x)$ is $3^n$ , well you can guess that $f^n(x) -2$ will have $\frac{3^n-1}{2}$ double roots and 1 simple root, for a total of $\frac{3^n-1}{2} +1$ roots. This gives the answer $\frac{3^{16}-1}{2} +1 = \fbox{21523361}$