Spongy Cuboid
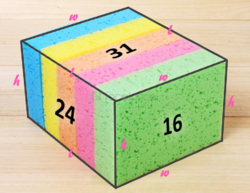 On each face of a cuboid, the sum of its perimeter and its area is written. The numbers recorded this way are 16, 24, and 31, each written on a pair of opposite sides of the cuboid. The volume of the cuboid lies between
__________
.
On each face of a cuboid, the sum of its perimeter and its area is written. The numbers recorded this way are 16, 24, and 31, each written on a pair of opposite sides of the cuboid. The volume of the cuboid lies between
__________
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Another approach is to add 4 to (1), to get that ( l + 2 ) ( b + 2 ) = 2 0 . Do you see how to continue from here?
Nice solution, @Karthik Sharma
Let the lengths of the distinct sides of the cuboid be x , y , z .
We see that the information given to us is the same as the following system of equations:
⎩ ⎨ ⎧ x y + 2 x + 2 y = 1 6 y z + 2 y + 2 z = 2 4 z x + 2 z + 2 x = 3 1
Adding 4 to each of the equations:
⎩ ⎨ ⎧ x y + 2 x + 2 y + 4 = 2 0 y z + 2 y + 2 z + 4 = 2 8 z x + 2 z + 2 x + 4 = 3 5
Factoring by Simon's Favorite Factoring Trick
⎩ ⎨ ⎧ ( x + 2 ) ( y + 2 ) = 2 0 ( y + 2 ) ( z + 2 ) = 2 8 ( z + 2 ) ( x + 2 ) = 3 5
Multiplying all the equations together and square rooting gives ( x + 2 ) ( y + 2 ) ( z + 2 ) = 1 4 0
Now we divide this by each of the equations to get:
⎩ ⎨ ⎧ x + 2 = 5 y + 2 = 4 z + 2 = 7 which means that ( x , y , z ) = ( 3 , 2 , 5 )
Thus the volume of the cuboid is 3 × 2 × 5 = 3 0
whoops sniped by Calvin.
x y + 2 ( x + y ) = 1 6
yz + 2(z+y) = 24
z x + 2 ( z + x ) = 3 1
Adding them,
x y + y z + z x + 4 ( x + y + z ) = 7 1
Now,
7 1 ≥ 3 x y z 3 2 + 1 2 x y z 3 1
Let x y z 3 1 = a
0 ≥ 3 a 2 + 1 2 a − 7 1
Therefore, a = 6 − 1 2 + 1 4 4 + 8 5 2
a ~ 3.2
x y z = a 3 = 3 2 . 7 6 8
Hence, maximum value of xyz is around 32.768
Therefore, xyz must lie between 28 and 35
@Kartik Sharma Yes, you are right. The exact value of a is 3.26, maximum volume would be 34.645. I think that assuming x,y and z to be positive integers gave the maximum volume 30.
(Its total coincidence that we have same first and last name with only difference being the letter 'h', approximately of same age, and discussing on the same problem on Brilliant)
Log in to reply
Hmm, are you in class 10?
Log in to reply
@Kartik Sharma No, I'm in 11th class. What about you?
Log in to reply
@Karthik Sharma – I am in class 10 actually though.
Log in to reply
@Kartik Sharma – @Kartik Sharma Nice HOUSE M.D. avatar!
Kinda spooky and looks like Adolf Hitler when the image is little.
Log in to reply
@Karthik Sharma – LOL House looks like Hitler. Just like Kartik looks like Karthik(the avatars too). Well, have you watched House?
Let l,b and h be the length, breadth and height of the cuboid respectively.
From the given information,
2 ( l + b ) + l b = 1 6 ... (1)
2 ( b + h ) + b h = 2 4 ... (2)
2 ( h + l ) + h l = 3 1 ... (3)
Solve (1) and (2) to get ( l − b ) ( 2 + h ) = 7 ...(4)
Solve (2) and (4) to get 4 l − 5 b = 2
Solve (1) and last equation to get b = 2 , l = 3 and c = 5
So the volume of the cuboid = l b h = 3 0