CM Punk
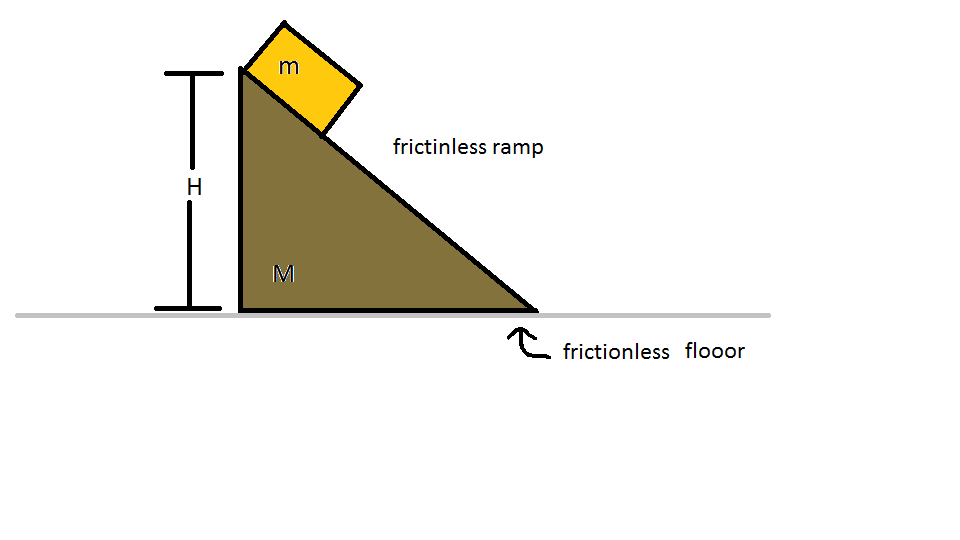
A mass of the block is m while that of the wedge is M every contact surface is frictionless.
Find the distance traveled by wedge as the block has reached the bottom given that the angle of the wedge is θ .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Considering the block and the wedge as my system .. since there is no external force the position of center of mass should not change. ... so as the block reaches the end it has moved hcot (theta) with respect to wedge ..... assuming wedge moved x..... movement of block with respect to ground should be equal to that of wege ... since center of mass does not change.... mH(HCot (theta)-x)=Mx
we will consider movement in only x axis taking tan θ = b a s e H we get base as H cot θ we are concerned with the base is the distance traveled by small block in the x axis with respect to the wedge so the actual distance traveled by the block will be distance traveled by block with respect wedge + distance traveled by wedge as we took the distance traveled by wedge as X but wedge moves in the opposite direction to block so apparent distance = H cot θ - X now come to c\point of center of mass since there is no force for my system in x axis the position of center of mass does not change F.Y.I we actually don't need to know the actual position of the center of mass just assume it to be at origin {where it may be} but as even after block reaches bottom it is remains at origin so m(h cot θ - X )=M X
we have to consider the movements in x axis only .... the block did come down via the hypotenuse but the displacement( of block with respect to wedge ) in the x axis is THE BASE. the actual distance traveled by the block can be understood as the displacement the block was supposed to be moving ( if the wedge was stationary ) - displacement by wedge ( we are subtracting it as the movement of wedge decreases the supposed displacement of the block ) .. the displacement of block gets X less ; than it was supposed to be ( if the wedge was stationary ) i.e it would have moved H cot θ but was pulled back by X (cause wedge moved) apparent distance = H cot θ - X
@Jaswinder Singh You should (previously) been able to submit a solution at the top of this page, once you got the problem correct (which you did as the problem creator). I've created a solution for you, can you edit it accordignly?
Can we take the force normal reaction as mg cos x ?
Any Solution Any one !!!!!!!!!!!!!!
Considering the block and the wedge as my system .. since there is no external force the position of center of mass should not change. ... so as the block reaches the end it has moved hcot (theta) with respect to wedge ..... assuming wedge moved x..... movement of block with respect to ground should be equal to that of wege ... since center of mass does not change.... mH(HCot (theta)-x)=Mx
Log in to reply
How you know it moved H cot (Theta),
Could you please add some more lines of Algebraic Approach
Log in to reply
we will consider movement in only x axis taking tan θ = b a s e H we get base as H cot θ we are concerned with the base is the distance traveled by small block in the x axis with respect to the wedge so the actual distance traveled by the block will be distance traveled by block with respect wedge + distance traveled by wedge as we took the distance traveled by wedge as X but wedge moves in the opposite direction to block so apparent distance = H cot θ - X now come to c\point of center of mass since there is no force for my system in x axis the position of center of mass does not change F.Y.I we actually don't need to know the actual position of the center of mass just assume it to be at origin {where it may be} but as even after block reaches bottom it is remains at origin so m(h cot θ - X )=M X
Log in to reply
@Jaswinder Singh – T h a n k s n i c e ! ! ! !
@Jaswinder Singh – @Jaswinder Singh Could you add that as a solution to this problem? Then I can delete this existing solution.
Log in to reply
@Calvin Lin – i m sorry i am not quite sure how to do that.... can you please explain
Log in to reply
@Jaswinder Singh – Jaswinder Singh I had a slight problem and would be grateful if you could please help me. My method ( S is displacement): S B W = S B − S W S W = S B W + S B However, I couldn't understand what S B W and S W should be. Should S B be the hypotenuse of the wedge? And what should S B W be? Many thanks in anticipation.
Log in to reply
@User 123 – we have to consider the movements in x axis only .... the block did come down via the hypotenuse but the displacement( of block with respect to wedge ) in the x axis is THE BASE. the actual distance traveled by the block can be understood as the displacement the block was supposed to be moving ( if the wedge was stationary ) - displacement by wedge ( we are subtracting it as the movement of wedge decreases the supposed displacement of the block ) .. the displacement of block gets X less ; than it was supposed to be ( if the wedge was stationary ) i.e it would have moved H cot θ but was pulled back by X (cause wedge moved) apparent distance = H cot θ - X
Log in to reply
@Jaswinder Singh – Thanks for your response. Sorry, but I have a few more doubts. I couldn't understand why we consider only the X -axis. Also, according to me, S B W X = S B X − S W X = H c o t ( x ) − X Am I correct?
Log in to reply
@User 123 – there is no external force acting horizontally.......gravity is acting vertically...... so as there is no external force horizontally the horizontal position of the center of mass does not change ( with help of which we equate displacements )
...........can you plz correct the editing
Log in to reply
@Jaswinder Singh – Thanks. I have edited the comment. Could you please have a look?
Log in to reply
@User 123 – i guess the original approach is getting a bit complex so i m gonna introduce another easier one .... since the forma for center of mass for system of object M and m at distance X1 and X2 from origin is given as ... m + M M ∗ X 1 + m ∗ X 2 .. for the question it becomes .... ( m(H cot θ - X )-M X )/(m+M) negative for M as it move sin opposite direction ... but we took Center of mass as origin so equate the equation to zero
@Jaswinder Singh – Thanks for your response. Sorry, but I have a few more doubts. I couldn't understand why we consider only the X -axis. Also, according to me, S B W X = S B X − S W X = H c o t ( x ) − X Am I correct?
The force that act on the block of mass m is the weight force W m ; the normal component of weight force W m n = m g cos θ is equilibrate by the reaction of the vinculus (ramp), hence the nect force directed towards the ramp is: W m p = m g sin θ ; If ( O , x , y ) is a system of cartesian coordinates with x towards the floor, y perpendicular at the floor and r the direction parallel to the ramp of the wedge, the force acting on the block is by 3rd law of dynamics the orizzontal component of the reaction (the vertical component is blocked by the vinculus of the floor) is: F x = m g sin θ cos θ ; ( 1 ) The acceleration of the wedge is: a x = M + m F x ; ( 2 ) The kinematic law of the motion with constant acceleration a x for the wedge leads to: x = 2 1 a x t 2 = 2 1 M + m m sin θ cos θ t 2 ; ( 3 ) The space covered by the block in the same time is: S = sin θ H = 2 1 a r t 2 ; a r = m m g sin θ = g sin θ ; ( 4 ) sin θ H = 2 1 g sin θ t 2 ; ( 5 ) Equating t 2 from ( 3 ) and ( 5 ) , we get: t 2 = 2 m g sin θ cos θ M + m x = 2 g sin 2 θ H ; x = M + m m H sin θ cos θ ; x = M + m m H cot θ