Co... Co... Company
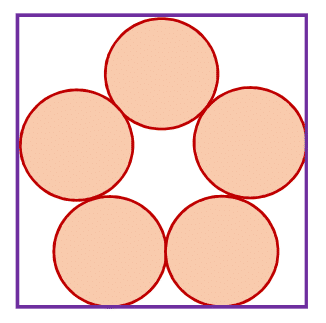5 unit circles are arranged within a square as shown.
What is the side length of the square, to 3 decimal places?
The answer is 5.149.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
There's a typo at line 1 where you said that A D = 2 × E B = x , which A D = x , but E B is
Also in the third line, you forgot to put comma
btw, your problem is great
there is nothing wrong on your approach! beautiful representation of Neoplatonismic Geometrical concept, i totally appreciate !
Did you solve the equation by hand?
5.236 was the answer i got, also how do you get A D = 2 E B ?
Log in to reply
EB goes from the mid line to the center of the circle on the right. 2 EB is the distance between the centers of the circles farthest left and farthest right. Add to that 1 on each side and you have the length of the base of the square. AD is the distance between the centers of circles farthest up and down. Add to it 1above and below and you have the height of the square. Since it is a square, the base and height must be equal.
Log in to reply
how i did it was :
1)The centers of the circle when connected form a regular pentagon of side 2
2) so < D C B = 1 0 8 ∘ and so < B C F = 7 2 ∘
3) thus side length of square is 4 + 2 ( 2 cos 7 2 ∘ ) = 5 . 2 3 6 0 6 7 9 7 7 5
can u tell me where i am wrong?
Log in to reply
@Anirudh Sreekumar – A regular pentagon would be wider than it would be high. Therefore the square required to contain it would be larger than the smallest such square. (As you shown it indeed is.)
The answer is indeed 5.236 as one of them has mentioned
That is the answer you get if you assume, incorrectly, that the centers of the circles form a regular pentagon. Circles which are tangent to a square, as shown in figure, form a pentagon which is slightly stretched in the upward direction. If it were not, the top circle would not be tangent to the square (or the bottom two would not be.). What you posted is not a solution because the problem calls for the smallest square and yours is larger than the solution provided above.
You should do a report instead
If points A, B, and C are centers of the top and right circles, then D C = 1 , C B = 2 , and B A = 2 . For the square to fit tightly, we need A D = 2 × E B . We'll set E B = x .
Using Pythagorean theorem in △ A B E , we get A E = 2 2 − x 2 .
In the △ C B F C F = x − 1 , C B = 2 , B F = 2 x − A E
Writing the Pythagorean theorem for the △ C B F will give us the equation
( x − 1 ) 2 + ( 2 x − 4 − x 2 ) 2 = 4
Only one of the solutions of this equation, namely x = 1 . 5 7 4 5 , is applicable to the problem.
The side of the square is 2 x + 2 = 5 . 1 4 9 .