Co-Normal Parabolic Centroid
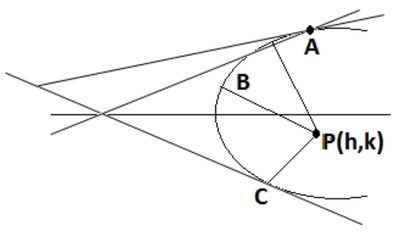
Centroid of triangle formed by three Co-Normal points A ( x 1 , y 1 ) , B ( x 2 , y 2 ) and C ( x 3 , y 3 ) on parabola y 2 = 8 x is G ( 4 , 0 ) . Two of the three points A , B and C lie above the x-axis or one of the point lies on x-axis. The normals drawn on parabola y 2 = 8 x at A , B and C are concurrent at M ( h , k ) .
If h = a and k > b , enter answer as a 2 + b 2 .
All of my problems are original
The answer is 116.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Aryan Sanghi
A very nice problem and a nice solution thanks for posting.
Upvoted.
Log in to reply
Thanku @Lil Doug
Log in to reply
@Aryan Sanghi
welcome.
I want you to upload more coordinate geometry hard problems.
Thanks in advance.
Log in to reply
@Talulah Riley – Sure, I'll try to make more problems. :)
Log in to reply
@Aryan Sanghi – @Aryan Sanghi and I will try to post solutions :)
@Aryan Sanghi A nice problem. Loved how you made this. Keep up the good work
@Aryan Sanghi
You just reuploaded the problem bro.
There is nothing wrong in the previous one.
Log in to reply
I am deleting the previous comment as people will know the answer else. :)
Log in to reply
@Aryan Sanghi can we again rewrite thoose comments also?
The equation of the normal to the parabola at the point ( 2 t 2 , 4 t ) is t x + y = 4 t + 2 t 3 . Thus M ( h , k ) lies on three normals provided that the cubic equation f ( t ) = t 3 + ( 2 − 2 1 h ) t − 2 1 k = 0 has three real roots. It these three roots are t 1 , t 2 , t 3 , then t 1 + t 2 + t 3 = 0 and t 1 t 2 + t 1 t 3 + t 2 t 3 = 2 − 2 1 h , and hence t 1 2 + t 2 2 + t 3 2 = h − 4 . Thus the centroid of A , B , C is G with coordinates ( 3 2 ( t 1 2 + t 2 2 + t 3 2 ) , 3 4 ( t 1 + t 2 + t 3 ) ) = ( 3 2 ( h − 4 ) , 0 ) and hence we deduce that h = 1 0 . Thus f ( t ) = t 3 − 3 t − 2 1 k has turning points at ± 1 .
For f ( t ) to have at least two non-negative roots, we need f ( 0 ) ≥ 0 > f ( 1 ) , which implies that − 4 < k ≤ 0 . Thus a = 1 0 and b = − 4 , making the answer 1 1 6 .
As always, excellent solution sir. Thanku for sharing it with us. :)
Comparing the equation y 2 = 8 x with y 2 = 4 a x , we get a = 2
Let the points be A ( 2 t 1 2 , 4 t 1 ) , B ( 2 t 2 2 , 4 t 2 ) , C ( 2 t 3 2 , 4 t 3 ) . Let the points A and B lie above x-axis. As the points are co-normal, so t 1 + t 2 + t 3 = 0
The normals at the points are concurrent at M ( h , k ) ≡ M ( 2 a + a ( t 1 2 + t 2 2 + t 1 t 2 ) , − a t 1 t 2 ( t 1 + t 2 ) ) . The centroid of the triangle is G ( 3 a ( t 1 2 + t 2 2 + t 3 2 ) , 0 ) .
Comparing, with centroid, we get
3 a ( t 1 2 + t 2 2 + t 3 2 ) = 4
3 2 ( t 1 2 + t 2 2 + ( − t 1 − t 2 ) 2 ) = 4 . . . . . . ( As t 1 + t 2 + t 3 = 0 )
t 1 2 + t 2 2 + t 1 t 2 = 3
So,
h = 2 a + a ( t 1 2 + t 2 2 + t 1 t 2 )
h = 1 0
Now, applying AM-GM inequality , we get
3 t 1 2 + t 2 2 + t 1 t 2 ≥ 3 t 1 3 t 2 3
1 ≥ t 1 t 2
t 1 t 2 ≤ 1 … ( 1 )
Now,
t 1 2 + t 2 2 + t 1 t 2 = 3
( t 1 + t 2 ) 2 = 3 + t 1 t 2 ≤ 3 + 1 … ( By ( 1 ) )
( t 1 + t 2 ) 2 ≤ 4
t 1 + t 2 ≤ 2 … ( 2 )
By ( 1 ) and ( 2 )
t 1 t 2 ( t 1 + t 2 ) ≤ 2 k = − a t 1 t 2 ( t 1 + t 2 ) k > − 4
Therefore, h = a = 1 0 and k > − 4 = b
So, a 2 + b 2 = 1 1 6