Cody vs Zi Song

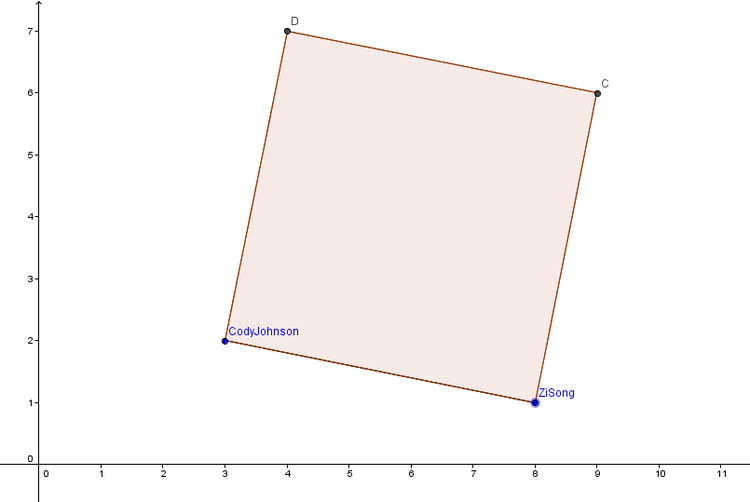As shown in picture , Cody Johnson is hovering in air at the point A(3,2) and Zi Song Yeoh is at the point B(8,1) . Cody should fly to Zi Song in such a way that when his path is drawn with magic pencil (which can draw in air) and the segment showing his displacement is drawn , the complete figure is a square (an example is shown in figure, Path is A-D-C-B) .

In how many ways can Cody go to Zi Song ?

Note :- If you want to know whether Cody is interested in going to Zi Song or not, you should read this problem Bromance <3

Trolling the Troller is BIG fun !

Details :-

$\bullet$ As the path will be square , Cody must move along exactly 3 line segments, without repeating the path.....(Like ABCDABCDABCD won't be a valid path)

$\bullet$ $1^{st}$ segment will start from point (3,2). $2^{nd}$ segment will be perpendicular to $1^{st}$ and $3^{rd}$ and $3^{rd}$ will have (8,1) as an endpoint . The displacement segment is segment joining (3,2) and (8,1) .