Tangle with triangle
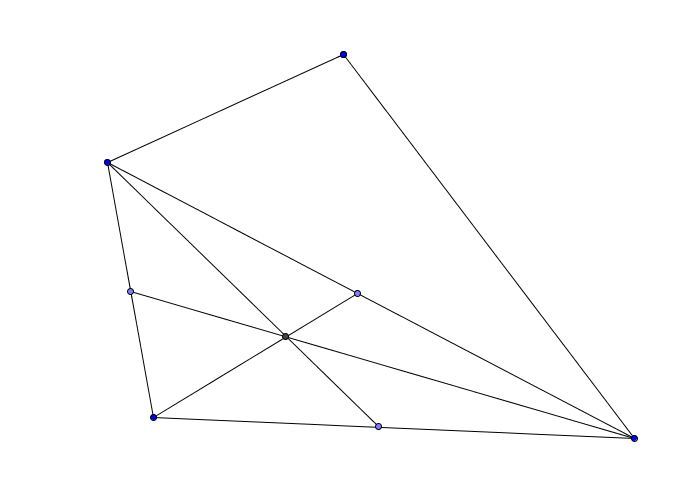 Let
Δ
A
B
C
be a triangle with vertices
A
,
B
&
C
and
D
,
E
&
F
be the midpoint of sides
A
B
,
B
C
&
C
A
respectively.
Let
Δ
A
B
C
be a triangle with vertices
A
,
B
&
C
and
D
,
E
&
F
be the midpoint of sides
A
B
,
B
C
&
C
A
respectively.
If A E = 2 . 5 , C D = 1 3 and B F = 2 7 3 , and P be the image(reflection) of point A about side B C .
Then find the area of the quadrilateral A B P C
Note the given picture is not necessarily correct.
Try more of my geometry here .
The answer is 12.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Aniket Verma @Purushottam Abhisheikh . Friends you can get this problem very easily . Thanks!
Log in to reply
Ya actually while thinking this question I forgot this formula and proceeded in a bit lengthy way that's why i posted it in level 5. BTW thanks for reminding me about this formula...
Log in to reply
@Vaibhav Prasad how did you do it?
Log in to reply
@Adarsh Kumar – @Adarsh Kumar The area of a triangle = 3 4 times the area of the triangle formed by it's medians.
Log in to reply
@Vaibhav Prasad – Ok!Thanx for replying!Sorry for the late reply,power was out since yesterday 8 30 PM.
@Adarsh Kumar – I used the formula that median of a triangle Δ A B C through its vertex A is equal to 2 b 2 + 2 c 2 − 4 a 2
And formed three equations to find the sides of the triangle...
Quite lengthy ...
Hey! Do u remember posting a question and deleting it soon afterwards ? (It happened a few days ago)
Check out it's disputes .
Log in to reply
Which question? Give me the link...
Log in to reply
Hey!Nihar,did you copy that combi question of yours (that 21,31,41..) from 102 combinatorial problems book?
Log in to reply
@Adarsh Kumar – Yeah! But I didn't "copy" it , I "shared" it.
I did not get the link :/ @Azhaghu Roopesh M
Log in to reply
OK , no problem . Just participate in OPC 3 and I'll get back to u later.
Log in to reply
@A Former Brilliant Member – You are not participating in OPC 3? :( :( :(
Log in to reply
@Nihar Mahajan – IDK , still got some exams to go . The deadline's the 15th right ? I'll see .
If u are on G+, u can catch up with me . I'll be checking thaat out once every day .
Cya!
I used coordinate geometry
Let A(0,a) B(-b,0) & C(c,0)
Then E((c-b)/2,0) D(-b/2,a/2) & F(c/2,a/2)
Using diatance formula we get following equations :
b²+c²-2bc+4a²=25....(1)
4b²+c²+4bc+a²=73....(2)
b²+4c²+4bc+a²=52....(3)
From (2) & (3),
b²-c²=7 &
5b²+5c²+8bc+2a²=125
5(b²+c²-2bc)+18bc+2a²=125
5(25-4a²)+18bc+2a²=125
a²=bc
Plugging this in (1) we get (b+c)²=25 or b+c=5
Hence b-c=7/5
b=16/5, c=9/5 & a=12/5
Area of ABC is 1/2 x (b+c) x a= 6
Area of quad ABPC is 2ABC=12
There is another formula which can be applied to find out the area of a triangle. Let A be = (m1 + m2 + m3)/2, where m1, m2, m3 are the medians of the triangle. Then area of the triangle is given by the following expression:
4/3 x [(A)(A - m1)(A - m2)(A - m3)]^1/2
Sorry guys, still did not learn LaTex :(
I have the best way to learn L A T E X !
Just hover ur cursor over L A T E X codes of others and u'll be a master at it in no time !
Log in to reply
@Azhaghu Roopesh M Yup thats a good idea.. By the way, you are there in the Brilliant Hangouts group right? We shall talk there :)
Log in to reply
Well , I had to leave it due to some reasons , add me back in !
Log in to reply
@A Former Brilliant Member – Okay.. I will do it tomorrow
Area of triangle A B C where u , v , w are its medians is given by :
3 1 [ 2 ( u 2 v 2 + v 2 w 2 + u 2 w 2 ) − ( u 4 + v 4 + w 4 ) ]
Substituting the values of medians , we get
A ( A B C ) = 6
Since , one of vertices of triangles is refected , it can be proved easily by congruence that :
A ( A B C ) = A ( B P C ) = 6
⇒ A ( A B C P ) = A ( A B C ) + A ( B P C ) = 1 2