Coloring Tetrahedrons

Geometry Level 1

There are 2 identical regular tetrahedrons. Each is painted with 1 red face, 1 blue face, 1 green face, and 1 yellow face.

Will they always be painted in the same way?

Clarification : They are painted in the same way if you cannot tell them apart from each other.

Yes, always No, not necessarily

3 solutions

Marta Reece
Jun 8, 2017

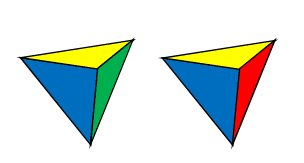If we place the blue and yellow in the same positions, we can have one tetrahedron showing green and the other red. The red and green could be exchanged for one another by a reflection, but not by a rotation. The tetrahedrons are mirror images of each other and are different.

@Agnishom Chattopadhyay To me, "not necessarily" implies that sometimes you can and sometimes you can't. In this case, you can never rotate them. I think the option should be "No, never" instead.

Calvin Lin Staff - 4 years ago

What I mean is that this is supposed to be for two arbitrarily colored tetrahedrons with four colors, not just the problem instance which is given

Agnishom Chattopadhyay - 4 years ago

Ah ic. Cool then :)

Calvin Lin Staff - 4 years ago

Forgive me if this is nitpicking, but I think the problem ought to say "2 identical regular tetrahedrons". If they aren't regular, then it is obvious that the answer will be "No, not necessarily."

Peter Byers - 3 years, 11 months ago

Another interesting question to ask would be how many such distinct possible tetrahedrons are there?

Agnishom Chattopadhyay - 3 years, 11 months ago

Only those two pictured in the solution. All others can be rotated to match them.

Marta Reece - 3 years, 11 months ago

Yep, and then we can generalize further by trying to lift this idea to other arbitrary symmetries. This then leads to Polya-Redfield Counting

Agnishom Chattopadhyay - 3 years, 11 months ago

This is the type of problem I can easily get through common sense / visualization but then feel I am cheating myself by not using any math. Is there a way to frame this as a permutation, either by "unfolding" / flattening the tetrahedron and then viewing it as a rotation? I visualize it as a circular permutation of three items (three triangles) around an unchanging central item (since the rotation or reflection does not affect the central item). This would lead to (3-1)! Permuatations around the center / circle, i.e. 2 distinct arrangements. Technically any of them can be the center triangle depending on how we choose to flatten / unfold it. This is easy to conceptualize and visualize, but I'm not satisfied. The main reason is that in 2 dimensions it's possible to make 8 combinations (I think), because each of the 4 colors could be at the center, and each central color can have 2 distinct permutations in a circle around it. How can I mathematically account for the introduction of the 3rd dimension? Clearly eliminating one of the variables works but I'm not sure why yet... Can someone help?

Hans G - 3 years, 11 months ago

We can arbitrarily pick color 1, let's say yellow. Every tetrahedron colored with the four colors has one face yellow, and it can be rotated so that this face is on top.

We can then pick color 2, for example blue. This color is adjacent to the yellow triangle since all three remaining colors are adjacent to that triangle. We can rotate the tetrahedron until the blue triangle is on the right.

The two remaining colors then occupy the two remaining locations. Their position, however, is not determined and they can be in two possible configurations, as pictured. The two configurations are mirror images of each other and cannot be made to coincide by rotation.

So two arbitrarily chosen tetrahedrons with all four colors may, but may not, have the same coloring.

Marta Reece - 3 years, 11 months ago

Thank you, and yes that is how I determined the correct answer as well. but I think there is a way to model this with group theory (a topic I am only beginning to learn).

Hans G - 3 years, 11 months ago

@Hans G – Let me know if you come up with one, I would be interested.

Marta Reece - 3 years, 11 months ago

@Hans G – Yes, there is a way to model this with Group Theory. What we are doing is essentially counting the number of orbits of a group action on a set. See Polya Enumeration Theorem and Burnside's Lemma . Looks like there is also a Brilliant Exploration about Burnside's.

Agnishom Chattopadhyay - 3 years, 11 months ago

David Orrell
Jun 19, 2017

This is the same reason we get optical isomers in chemistry about a chiral centre - there are two nonsuperimposable mirror images possible in this tetrahedral arrangement

Moderator note:

The chiral forms are called L (for the Latin word laevus meaning "left") and D (for the Latin word dexter meaning "right").

Like trying to fit your left hand over your right hand:)

Dan Ley - 3 years, 11 months ago

This Problem remembered me of my chemistry lessons too. It's interesting how these topics are related.

Maximilian Zobel - 3 years, 11 months ago

Surya Subbarao
Jun 19, 2017

Given three colors, we can color the top three faces each with one of those three colors and color the bottom face the left over color, and whatever way you choose what top face gets what color, the colorings would be identical. However, there are 4 ways to choose 3 colors, so there are in fact 4 different colorings possible.

I think there are only two. Since every face shares an edge with other face you can align two tetrahedral such that the yellow and blue faces are in the same position. What remains is two options for colouring the other two faces.

Malcolm Rich - 3 years, 11 months ago

Up to rotation there are only two ways to choose 3 colors.
You're better off fixing the bottom color (say, yellow) and then notice that you only have two choices: red-blue-green clockwise or red-green-blue clockwise. Just notice that red-blue-green is the same as blue-green-red and green-red-blue, and that red-green-blue is the same as green-blue-red and blue-red-green.

Richard Desper - 3 years, 11 months ago

If we calculate all possibilities we can find 4.3.2.1 = 24 Then we should find same possibilities, for one possibility, are 4.3 = 12 possibilities. So we should divide 24 into 12 and we found 2.

Arman Özcan - 3 years, 11 months ago

Coloring Tetrahedrons

3 solutions

Moderator note:

0 pending reports