Colouring Space

Probability Level 3

You have a 3D pen which has three colours $\color{#D61F06}{\text{Red}} , \color{#3D99F6}{\text{Blue}} , \color{#20A900}{\text{Green}}$ . I give you a $2\text{m}\times2\text{m}\times2\text{m}$ cube and ask you to completely fill it with the colours in such a way that no two points in the cube which are $1\text{m}$ apart have the same colour. Is this possible? If it is possible, how many ways can this be done?

Yes, it is possible in only

6

ways Yes, it is possible in

48

ways Yes, it is possible in

6! \times 8

ways Yes, it is possible in

48!

ways No, it is not possible

1 solution

Chris Lewis
Feb 26, 2021

This actually isn't even possible in the plane, never mind a cube.

The three vertices of any $1$ m equilateral triangle have to be different colours. Draw such a triangle, then add a new equilateral triangle on one of its sides: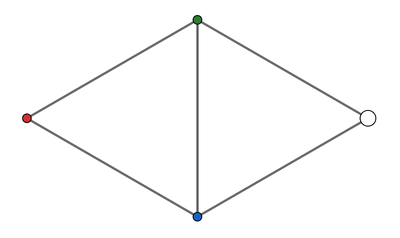

The blank circle on the right can only be coloured red (it's one metre from a green point, and one metre from a blue one). Note the order of the colouring is arbitrary.

We conclude that any two points separated by a distance of $\sqrt3$ m must have the same colour .

But now consider an isosceles triangle with sides $\sqrt3$ , $\sqrt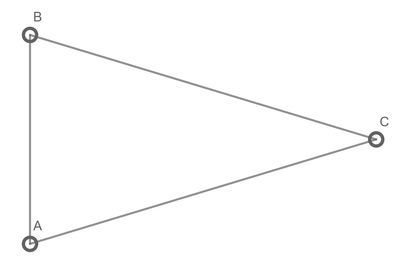3$ , $1$ metres:

Points $A$ and $C$ must be the same colour (separated by $\sqrt3$ m); points $B$ and $C$ must be the same colour; but points $A$ and $B$ (separated by $1$ m) can't be. Contradiction!

So the colouring is impossible.

Nice solution, I wanted the problem to be easily solvable by considering a tetrahedron