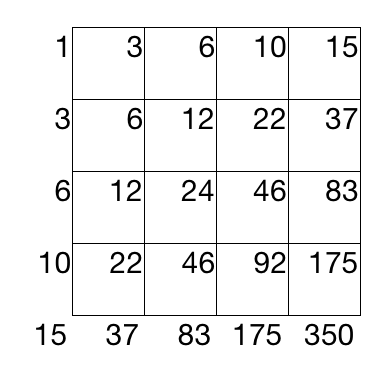
Operator Square

Set up the summation on a grid, to ensure that we get the proper numbers.

The first rule tells us the first horizontal row.
The second rule tells us the first vertical row.
The third rule tells us that each cell is obtained by summing up the cell above it and the cell to the left.

Hence, we get

Read Kevin Chung's solution to understand how to solve this particular problem.
The general solution to the recurrence relation is $a \square b = { a + b \choose a } - { a + b - 2 \choose a-1 }$ , which we can prove by induction and checking all the $1 \square n, n \square 1$ base cases. However, this would make the formula seem like magic.
This solution explains how pascal's triangle can be applied to solve this recurrence relation problem type and obtain the formula.

Consider the following operator $\oplus$ .

• $a \oplus b = 0$ if $a < 0$ or $b < 0$
• Seed: $0 \oplus 0 = {\color{#D61F06}1}$
• $a \oplus b = a \oplus (b-1) + (a-1) \oplus b$

By setting it up in a triangle-form, we get the following:

$\begin{array} { cccccccccccc} & & & & & {\color{#D61F06}1} & & & & & \\ & & & & 0+1=1 & & 1+0=1 & & & & \\ &&& 0+1=1 && 1+1=2 &&1+0=1 &&&\\ && 0+1=1 && 1+2=3 && 2+1=3 && 1+0=1 && \\ \end{array}$

Thus, we see that the $\color{#D61F06} 1$ helps us to generate the Pascal's triangle, and we obtain that each term is of the form ${ a + b \choose a }$ .

How do we adapt it to the scenario in the question? The trick is to find suitable places seed $\color{#D61F06} 1$ that would lead us towards the desired result. It's not currently obvious what we could do, so let's analyze the given scenario further:

$\begin{array} { ll llllllllll} & & & & & 1 & & & & & \\ & & & & 2 & & 2 & & & & \\ &&& 3 && ? && 3 &&&\\ && 4 && ? && ? && 4 && \\ & 5 && ? && ? && ? && 5 \\ 6 && ? && ? && ? && ? && 6 \\ \end{array}$

The issue here is that the sides of the triangle are not 1, and so we cannot find the $\color{#D61F06} 1$ to seed the pattern. However, notice that the sides are identical to the 2nd row of Pascal's triangle, so that suggests that we could backtrack to find our $\color{#D61F06}1$ . Let's work with the left side first.

$\begin{array} { ll llllllllll} & & & & {\color{#D61F06}1} & & & & & \\ & & & {\color{#3D99F6}1} && 1 & & & & & \\ & & {\color{#3D99F6}1}& & 2 & & 2 & & & & \\ &{\color{#3D99F6}1}&& 3 && ? && 3 &&&\\ {\color{#3D99F6}1}&& 4 && ? && ? && 4 && \\ \end{array}$

This looks great! We've found a potential seeding point. Now, let's observe what happens if we tried to do the same on the right.

$\begin{array} { ll llllllllll} & & & & {\color{#D61F06}1} & & {\color{#D61F06}1} & & & \\ & & & {\color{#3D99F6}1} && {\color{#69047E}1} & & {\color{#3D99F6}1}& & & \\ & & {\color{#3D99F6}1}& & 2 & & 2 & & {\color{#3D99F6}1}& & \\ &{\color{#3D99F6}1}&& 3 && ? && 3 &&{\color{#3D99F6}1}&\\ {\color{#3D99F6}1}&& 4 && ? && ? && 4 && {\color{#3D99F6}1} \\ \end{array}$

As you can see, if we tried to duplicate the same naively, we end up with the ${ \color{#69047E} 1 }$ having an incorrect value. It should have been $1 + 1 = 2$ , but instead we have it as 1 (and that affects all the subsequent values). How can we fix this? Well, let's add a seed of $-1$ at that spot!

With the following seed:

$\begin{array} { ll llllllllll} & & & & {\color{#D61F06}1} & & {\color{#D61F06}1} & & & \\ & & & && {\color{#D61F06}-1} & & & & & \\ \end{array}$

We will obtain:

$\begin{array} {cccccccccccc} &&&& {\color{#D61F06}1} && {\color{#D61F06}1} && \\ & & & 0+1=1 && 1+1+ {\color{#D61F06}(-1)} =1 & & 1+0=1 & & & \\ & & 0+1=1& & 1+1=2 & & 1+1=2 & & 1+0=1& & \\ &0+1=1&& 1+2=3 && 2+2=4 && 2+1=3 &&1+0=1&\\ 0+1=1&& 1+3=4 && 3+4=7 && 4+3=7 && 3+1=4 && 1+0=1\\ \end{array}$

Let the $\color{#D61F06} -1$ seed be in position $(1,1)$ , since that is what the $\square$ operator desires.
Consider the contribution of these seeds to the entry in $(a,b)$ .

The $\color{#D61F06} 1$ seed in position $(1, 0)$ will contribute $1 \times { (a-1) + b \choose (a-1) }$ .
The $\color{#D61F06} 1$ seed in position $(0,1)$ will contibute $1 \times { a + (b-1) \choose (b-1) }$ .
The $\color{#D61F06} -1$ seed in position $(1,1)$ will contribute $-1 \times { (a-1) + (b-1) \choose (a-1) }$ .
Hence, $a \square b = { a + b - 1 \choose a - 1 } + { a + b -1 \choose b-1 } - { a + b - 2 \choose a-1 }$ .

Note: We could have used a different seed of

$\begin{array} { ll llllllllll} & & & & & {\color{#D61F06}1} & & & & & \\ & & & & {\color{#D61F06}0} & & {\color{#D61F06}0} & & & \\ & & & && {\color{#D61F06}-1} & & & & & \\ \end{array}$

which leads to the equivalent (but nicer looking) formula ${ a + b \choose a } - { a + b - 2 \choose a-1 }$ .

Give this idea a try and see what you get. For example, how can we solve:

• $0 \otimes n = n^2$
• $n \otimes 0 = n$
• $a \otimes b = a \otimes (b-1) + (a-1) \otimes b$

In Rectangular Grid Walk, the number of ways an object can run through an $a\times{b}$ grid going only two directions is $\displaystyle {a+b \choose b}$ .

As the definition says $a\square{b}=a\square(b-1)+(a-1)\square{b}$ (when a,b >1) we can think of a $5\times5$ rectangular grid:

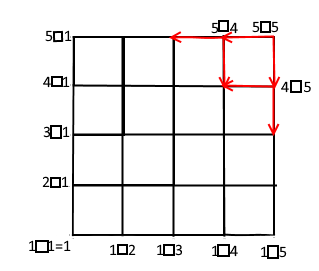
When we "shatter" the original $5\square5$ step by step with the previous rule, and the other two rules: $n\square1=(n-1)\square1+n$ and $1\square{n}=1\square{n-1}+n$ we see that $5\square1$ , $4\square1$ , $3\square1$ , $2\square1$ , $1\square5$ , $1\square4$ , $1\square3$ , $1\square2$ and $1\square1$ appear during the process as many times as there are possible ways to reach the dot representing them in the rectangular grid above. When this process is continued, each $n\square1$ and $1\square{n}$ produces the number $n$ in the final result as they are "shattered" by the rules $n\square1=(n-1)\square1+n$ and $1\square{n}=1\square{n-1}+n$ . Eventually we get these " $n$ :s" with each value of $n$ and a number of $1\square1$ :s, and there was the definition $1\square1=1$ .

For each positive integer $m$ and $n$ , the rectangular grid presenting $m\square{n}$ has the measures $m\times{n}$ in the amount of dots. In general, for each positive integer $a$ when $1<a\leq(m-2)$ , $(m-a)\square1$ appears $\displaystyle{n-1+a \choose a}$ times during the process, and for each positive integer $b$ when $1<b\leq(n-2)$ , $(n-b)\square1$ appears $\displaystyle{m-1+b \choose b}$ times. Each $(m-a)\square1$ produces an $m-a$ and each $(n-b)\square1$ produces an $n-b$ in the final result, so the previous values are multiplied with them and then summed together. Additionally, $1\square1$ is produced $\displaystyle{m+n-2 \choose n-1}$ times.

For example, there is one way to produce $m\square1$ with using the rules above, and $\displaystyle {n \choose 1}$ ways to produce $(m-1)\square{1}$ , judging by the formula for rectangular grid walk presented above in the start. Each $m\square1$ produces an $m$ when "shattering", and each $(m-1)\square1$ produces an $m-1$ when "shattering".

This means $m\square{n}=\sum_{k=0}^{m-2}((m-k)\displaystyle {n-1+k \choose k})+\sum_{k=0}^{n-2}((n-k)\displaystyle {m-1+k \choose k})+\displaystyle {m+n-2 \choose n-1}$

We get

$5\square5=2(1\times5+5\times4+\displaystyle {6 \choose 2}\times 3+\displaystyle {7 \choose 3}\times 2)+\displaystyle {8 \choose 4}\times 1=2(5+20+45+70)+70=2\times140+70=\boxed{350}$ .

Here is a straightforward way to run Chung Kevin's idea using Haskell:

1
2
3
4
5

f :: Int -> Int -> Int
f 1 1 = 1
f n 1 = n + f (n-1) 1
f 1 n = n + f 1 (n-1)
f n m = f n (m-1) + f (n-1) m 

Then, f 5 5 gives the desired result.