Combining charged caps
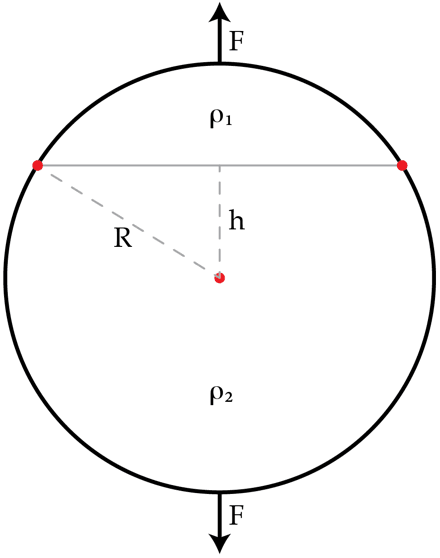
Two spherical caps with constant volume charge densities ρ 1 and ρ 2 are in contact and form a ball or radius R as shown in the figure. Find the force of interaction F between the caps in Newtons if ρ 1 = 1 × 1 0 − 3 C / m 3 , ρ 2 = 2 × 1 0 − 3 C / m 3 , R = 1 0 cm and h = 5 cm .
Details and assumptions
The vacuum permittivity is ε 0 = 8 . 8 5 × 1 0 − 1 2 F / m .
The answer is 3.33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Great...!! Hey @jatin yadav where did you studying now...??
Log in to reply
I am presently an engineering student at IIT Delhi
Log in to reply
At age of 16?
nice solution @jatin yadav , how can i be a good problem solver like you at physics especially EM,You are my inspiration pls suggest anything
Log in to reply
First, you need to study calculus(generally, 15 year olds don't know calculus).You should start studying a nice but basic electrodynamics book. Then , go to an advanced book( Jackson, for example). First make all your concepts clear and then try problems(in ascending order of difficulty). Ask your doubts to your teachers, or in form of notes here.
Log in to reply
thanks @jatin yadav i will do what you suggested,
good solution
I used the same method the only difference being the initial step i.e I considered a solid sphere of charge density rho1 and a small part of it has a charge density of rho2 - rho1..
Is it double integration you applied
Consider the case when whole of the sphere has charge density ρ . We will find the force of interaction in this case and then we will replace ρ 2 by ρ 1 ρ 2 to get the final answer(because the force between any two charge components would change in this way).
Let the electric fields due to th caps be E 1 and E 2 respectively.
Clearly , the force of interaction is
F = ∫ q ∈ cap 1 E 2 d q
Now as the sum of internal forces is 0 , hence,
∫ q ∈ cap 1 E 1 d q = 0
Hence,
F = ∫ q ∈ cap 1 ( E 1 + E 2 ) d q
We know that E 1 + E 2 = 3 ϵ 0 ρ r
Now,
Consider a small ring of radius y at height x above the center subtending an angle θ at the center. Clearly, cos θ = r x
Clearly, d F = 3 ϵ 0 ρ r × ρ × 2 π y cos θ d y d x
= 3 ϵ 0 2 ρ 2 π x y d x d y
Clearly, x varies from h to R , and y varies from 0 to R 2 − x 2
Hence,
F = 3 ϵ 0 2 ρ 2 π ∫ h R x ( ∫ 0 R 2 − x 2 y d y ) d x
= 3 ϵ 0 2 ρ 2 π ∫ h R x ( R 2 − x 2 ) d x
= 1 2 ϵ 0 ρ 2 π ( R 2 − h 2 ) 2
Replacing ρ 2 by ρ 1 ρ 2 , the force of interaction is :
1 2 ϵ 0 π ρ 1 ρ 2 ( R 2 − h 2 ) 2