Come right inside, please
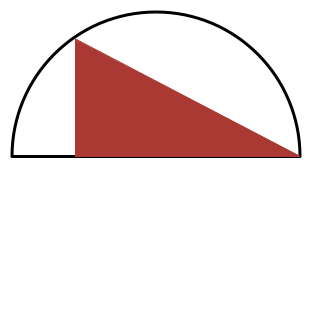 Let
S
be the maximum possible area of a right triangle that can be drawn in a semi-circle of radius
1
, where one of the legs (and not the hypotenuse) of the triangle must lie on the diameter of the semicircle.
Let
S
be the maximum possible area of a right triangle that can be drawn in a semi-circle of radius
1
, where one of the legs (and not the hypotenuse) of the triangle must lie on the diameter of the semicircle.
If S = c a b , where a , c are positive coprime integers and b is a positive square-free integer, find a + b + c .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I feel like adding this image to the problem. Do you approve?
Log in to reply
Yes, that would be great. Thanks. :)
Log in to reply
Well, not adding images to your problems benefits me more.
I go through special cases and sometimes accidentally find something interesting.
"How many circles can be drawn circumscribing a given triangle? How many triangles can a given circle circumscribe ?" I came across these this time.
How are you @brian charlesworth ?
Log in to reply
@Soumo Mukherjee – I'm doing well, thanks. Hope that you're doing well too. I haven't seen any activity from you on Brilliant the last few weeks; I was beginning to wonder where you'd gone.
I agree that sometimes it might actually be preferable not to have an image attached, so that creating a suitable diagram based just on the text becomes part of the solution process. At the same time, though, an image tends to grab people's attention, so that they are more likely to try the question. In this case the text is reasonably clear, so that the image doesn't give too much away while still having the ability to at least make people stop and give the problem some thought.
That being said, I'm glad that the question led you to formulate other problems to consider. For your first question, since any circle that circumscribes a given triangle must touch each of the triangle's three vertices, and since any three points uniquely defines a circle, there can be only one possible circle that circumscribes a given triangle. For the second question the answer would be an infinite number, but a follow-up question could be: given that a triangle is circumscribed by a circle, what is the probability that the triangle's area is less than, say, one-quarter the area of the circle? I don't know what the answer is off the top of my head, but it is nevertheless fun to think about how one would go about solving the problem.
Log in to reply
@Brian Charlesworth – I agree. Image, problem-statement as well as the person posting. Yes, people do get their attention directed to the person posting the problem.
"It's fine to work on any problem, so long as it generates interesting mathematics along the way - even if you don't solve it at the end of the day." This quote is from Andrew Wiles.
I was trying to "find the maximum area of a triangle which is inscribed in circle of radius 1 and then half it using the argument that a circle is symmetric about its diameter." In the pursuit those two questions came up.I didn't dig further.
It took me time and trial to hit upon the idea, and gather courage, to proceed by fixing any one vertex. I wan't sure about my method because the problem's condition possesses enough variety. I miscalculated and got a wrong answer. This was my 2nd try. In the first try I guessed the answer as 1 0 . I din't try 3rd time, I wasn't confident about my procedure.
There are exams in March and April I am spending time on preparation. I am having network problems with my broadband. Some days it is too slow. Some days it doesn't even work. I planned for clarifying doubts here-there are problem which I can't even understand. But my broadband won't allow it.
After 2/3 months my frequency on Brilliant may increase :) I miss this place.
Have a good day :)

Log in to reply
@Soumo Mukherjee – Sorry to hear about the problems with broadband; that must be really frustrating. And yes, it appears that everyone in India is focussing on those upcoming exams; good luck with your preparation for them and I hope that you get the results you are wanting. :)
Yea I need that for my solution. Thanks :)
The problem states that a, and b are co-prime which by definition means that they are only divisible by 1. in your solution a=b=3 therefore since they are both divisible by 3 they are not co-prime. Also 8 is not square free because it is divisible by 4=2*2 so I believe that this solution is wrong.
Log in to reply
Sorry! It was a typo; I'm surprised that no one caught it before now. Thanks for bringing it to my attention. I have edited the question to reflect my original intention that a , c are coprime and b is square-free. With this correction I hope that you find that the posted solution is correct.
I also apologize if the typo led to you not getting credit for solving the problem.
can you please explain why its (1+x) in your S formula. why isn't it just x ?
Log in to reply
As depicted in the diagram, the base of the triangle extends from the left end of the diameter to the vertex P at the right angle of the triangle. It is assumed that, for a right triangle of maximum area, P will lie to the right side of the midpoint O of the diameter. So the base of the triangle will have a length that is the sum of the radius of the semicircle and O P = x , which comes out to ( 1 + x ) .
Log in to reply
aaaaaaaaaaaaa it's radius + something else, I got it thanks. First I thought x would be the whole length
Btw, I have a similar problem to yours posted on my profile. You can try it out. It's very alike
I took a short cut to the problem, knowing that the triangle equilateral inscribed in a circunference yields the biggest area, half of such an equilateral triangle will do so in half circle. So the asking area S equals 3*sqrt(3)/8
I am in no doubt that your statement is correct, but how can you prove that an equilateral triangle creates the biggest area. Does it satisfy the upper bound of an inequality?
Log in to reply
That it is easy. Consider the area of the bigger circular segment above on of the side of our equilateral triangle. This side we will consider the base of all triangles we can inscribe inside the mentioned circular segment. The biggest chunk of area of the segment we can subtract will be from the triangle the one which altitude is higher , since all have the same base. Obviously that happen when you split the arc by the half.
Indeed the maximum area we can obtain from any n-polygon inscribed in a circle is a regular n-polygon, using same reasoning as above by taking the one vertex in between two and moving within the arc, To get the biggest area you must split the arc by the half.
Even you can choose n point at random in the circunference selecting them as vertexes of our n-poligon. Then we will relocate each points as midpoint of the arc between the to adjacent ones, by doing so by exhaustion we will end in regular polygon that also will yield the biggest area.
Log in to reply
Your reasoning is sound, and I did expect some solvers to take this intuitive approach. In some situations, however, when you remove a condition of symmetry, the resulting maximal result is no longer what one would have intuitively expected, which is why I always prefer to take a formal approach in order to either confirm intuition or discover an interesting exception.
Log in to reply
@Brian Charlesworth – Brian, above all I do admire your hard work, rigor, dedication and enthusiasm, a beacon of math light, wisdom and knowledge among an army of young math-alcoholics in which I include you.... Hopefully world will be better thanks to all of you.
But you see I am not a pro like most of you look to me, I am just old engineer and naval architect who try to enjoy the challenges of this enticing website and crack down the problems by using the least of the paper and pencil and the most of my ingenuity to fight against ruthless degradation of an aging brain.
Sometimes even I try to concentrate in those problems at the dentist chair in attempt not to think in the carnage going underway inside my mouth.
The math knowledge and resources tools I posses are limited, there are huge empty spaces much wider than the Great Lakes but I enjoy the challenges, so I will be around meanwhile health and time allow me so.
Log in to reply
@Mariano PerezdelaCruz – I enjoyed reading your comments, Mariano. I like your style and I appreciate the compliments. (Next time I'm in the dentist's chair I'll have to try your method of mind over matter. :))
The beauty of mathematics is that it involves a combination of creativity and rigor, not unlike what is involved in the design and construction of a beautiful vessel or building. (Both my parents were architects, (buildings, not boats), so I witnessed the process firsthand.) Rigor can be taught, but creativity is a more fickle attribute, and thus I hold those who have it in higher regard. I'm glad that you are here on this site sharing your interest and ingenuity. :)
@Mariano PerezdelaCruz – I did the problem the same way - by reflecting the figure to a full blown circle and take half of the resulting equilateral triangle. Though I enjoyed solving it thus, I did get pang of guilt for doing so.
I was checking if anyone had done it the same way and after finding your answer, started reading the thread. What you wrote here struck a chord. And now I am feeling much better. :-)
I realize, that doing away with rigor is not even remotely a wholesome way of doing math. And hope to acquire at least a humble fraction of the skills that you and Brian possess!
A similar argument (which I suspect is equivalent to what you stated), is that given 2 points on a circular arc, the area bounded between these 2 points and a third point on the circumference occurs when the third point is on the perpendicular bisector of these two point, and hence bisects the circumference into 2.
Since the set of triangles on a circle is continuous, and the area is bounded, hence there is a maximum which is achieved. Any triangle that is not equilateral cannot be the maximum, hence the maximum occurs for the equilateral triangle (respectively regular polygon).
same i have done
I took one vertex as (-1, 0), and one vertex on the circumference as (cost, sint) and the remaining is (cost, 0)
Draw the right-angled triangle in the semicircle where ∠ A B C = 9 0 , BC lies on the diameter and D is the centre of the semicircle. Now draw radius AD and let ∠ B D A = x . Now we have triangle ABD, where B D = c o s x a n d A B = s i n x . For triangle ADC, A D C = 1 8 0 − x . Now using area of a triangle = 2 1 absin(x) (or 2 1 base × height for triangle ABD) a r e a = 2 1 s i n x c o s x + 2 1 s i n ( 1 8 0 − x ) = 2 1 ( s i n x c o s x + s i n x ) = 2 1 ( 2 1 s i n ( 2 x ) + s i n ( x ) ) = f ( x ) ( f r o m s i n 2 x = 2 s i n x c o s x ) Differentiating the equation and equating it to zero to find a stationary point: f ′ ( x ) = 2 1 ( c o s 2 x + c o s x ) = 0 ⇒ c o s 2 x = − c o s x ⇒ 2 c o s 2 x − 1 = − c o s x ⇒ ( 2 c o s x − 1 ) ( c o s x + 1 ) ⇒ c o s x = 2 1 a s 0 < x < 9 0 ⇒ x = 6 0 Now differentiating again to find the nature of this stationary point: f ′ ′ ( x ) = − 2 1 ( 2 s i n 2 x + s i n x ) ⇒ f ′ ′ ( x ) < 0 ⇒ m a x p o i n t
∴ m a x [ f ( x ) ] = f ( x = 6 0 ) = 8 3 3
It should be clear that one vertex of the triangle of maximum area will coincide with one end of the circle's diameter, say the right side, and that the vertex P at the right angle of the triangle will then lie to the left of the center O of the diameter of the semicircle. Letting ∣ O P ∣ = x , and letting the vertical leg of the triangle extend up from P to intersect with the semicircle, the height of the triangle will then be 1 − x 2 . The area of the triangle is then
S = 2 1 ( 1 + x ) 1 − x 2 .
Now differentiate with respect to x and set the derivative equal to 0 :
d x d S = 2 1 [ 1 − x 2 − 1 − x 2 x ( 1 + x ) = 0
⟹ 1 − x 2 = x + x 2 ⟹ 2 x 2 + x − 1 = 0
⟹ x = 4 − 1 ± 1 + 8 = 4 − 1 ± 3 .
Since we want x > 0 we find that x = 2 1 , and thus
S = 2 1 ( 1 + 2 1 ) 1 − 4 1 = 8 3 3 ,
and so a + b + c = 3 + 3 + 8 = 1 4 .
(Note that it should also be clear that any critical points found in the differentiation process will yield a maximum, since we could let x = 1 to get a minimum of S = 0 .)