Comparing Areas!

$\dfrac{\color{#3D99F6}{\text{Blue Triangle}}}{\color{#20A900}{\text{Green Triangles}}} = \dfrac{\color{#3D99F6}{1}}{\color{#20A900}{26}}$

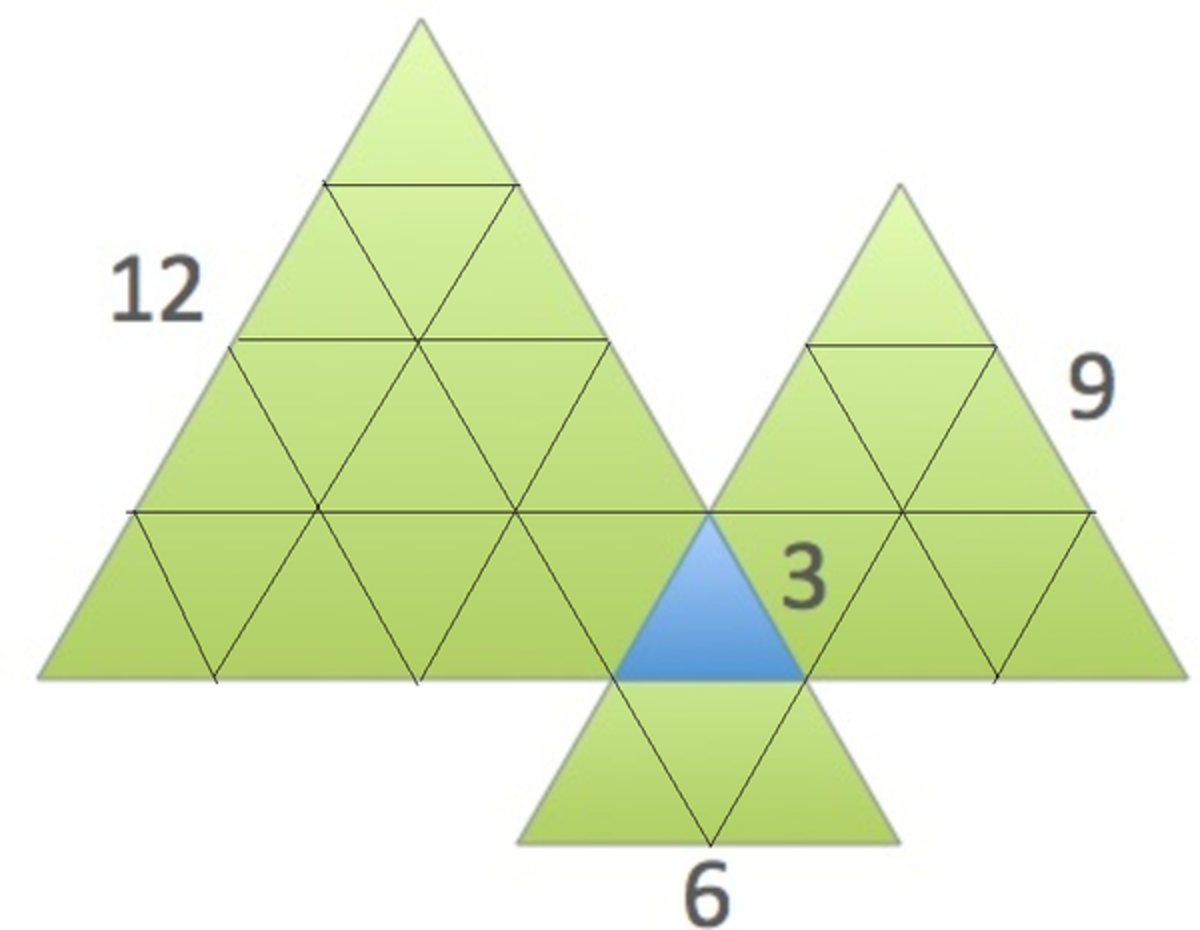A simple solution by dividing the graph into small triangles and notice the comparison.

Second Solution:

Area of any Equilateral Triangle is: $\frac{\sqrt{3}}{4}s^2$

Area of Green Triangles: $\frac{\sqrt{3}}{4}( 12^2+9^2+6^2) = \frac{\sqrt{3}}{4} (261)$

Area of Blue Triangle: $\frac{\sqrt{3}}{4} 3^2 = \frac{\sqrt{3}}{4}( 9)$

$\Large\frac{\text {Area of Blue Region}}{\text{Area of Green Region}} = \frac{ 9}{ 261-27} = \frac{1}{26}$

Keep in mind that one green triangle is repeated three times : That is why we subtract $27 = 3\times 9$ from $261$

The area of an equilateral triangle is proportional to the square of the side (with a proportionality constant of sqrt(3)/4, which is actually not relevant in this case because it will cancel in the quotient). The green area is the sum of the areas of the big triangles minus three times the area of the blue triangle. Therefore:

A(Blue) / A(Green) = (3^2) / (12^2 + 9^2 + 6^2 - 3*3^2) = 9/234 = 1/26.