Which Radical Difference Is Greatest?
Which is greater?
8 − 7 OR 6 − 5
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
27 solutions
Moderator note:
Good observation with the algebraic conjugates.
good order of thinking
This requires out of the box thinkling to solve, atleast for me.
How do u type these equations. I use Word to type equations. Is there any other free software available for typing mathematical equations
Log in to reply
there is formatting guide
LaTex is a good one.
We use L A T E X to generate these equations on Brilliant.You can learn it from here
I use Daum Equation Editor, it make more simple and give for you all the code to put in the site.. just search in google chrome store
I'm sure there are plenty of beautiful algebraic solutions to this. But I am a creature of habit, so I will be using calculus.
Both numbers take on the form f ( x ) = x + 1 − x . This function's derivative is f ′ ( x ) = 2 x + 1 1 − 2 x 1 ,
which is negative for all x > 0 , implying f ( x ) is decreasing on its entire domain and that f ( 5 ) > f ( 7 ) . Therefore, 6 − 5 > 8 − 7
"But I am a creature of habit, so I will be using calculus." Relatable.
Relatable too! I did the same thing except that I reflected upon how the difference of squares increases as numbers increase (eg. 8^2 - 7^2 is greater than 6^2 - 5^2) and then reasoned that the opposite would be true in the case of square roots.
Same! The following is my solution:
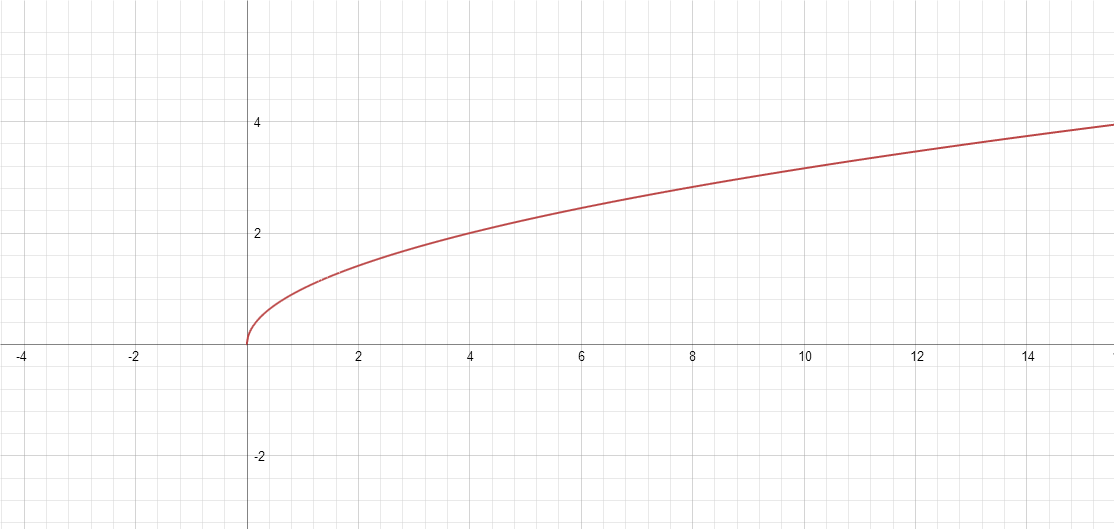
I did this graphically. The reasoning is that the function is concave down and increasing. When a function is concave down and increasing OR concave up and decreasing, the difference between successive terms decreases as x increases.
I pictured
f
(
x
)
=
x
. The larger value of
x
, the smaller the change between
f
(
x
)
and
f
(
x
−
1
)
. Therefore,
6
−
5
>
8
−
7
.
This is how I thought of it as well!
Different approach.. Superb.. I never imagined in this way
My method! :D
Exactly!!!
super sir super
De donde sale resultado?
Log in to reply
( 8 + 5 ) 2 = ( 8 ) 2 + ( 5 ) 2 + 2 8 5
8 − 7 ? 6 − 5 8 + 5 ? 7 + 6 Square both sides subtract 13 and divide by two to get 4 0 ? 4 2 4 0 < 4 2
and we are done.
Could you clarify how "we are done" when you post a solution? Most of the people who need to read the solutions aren't going to understand the process you used.
I assume your argument is that because the left side of the inequality is smaller than the right side at the end, then the left side at the beginning was smaller throughout, because none of the calculations would have changed the sign.
That type of detail is useful to point out, for those of us who are either learning or trying to remember how math works.
This is the only method I could understand well, and I upvoted for you
You can get some intuition from noting that d/dx of sqrt(x) is decreasing, but the proof is a lot of squares.
assume the right answer
8 − 7 < 6 − 5
( 8 − 7 ) 2 < ( 6 − 5 ) 2
8 − 2 5 6 + 7 < 6 − 2 3 0 + 5
4 < 2 5 6 − 2 3 0
2 < 5 6 − 3 0
( 2 ) 2 < ( 5 6 − 3 0 ) 2
4 < 5 6 − 2 5 6 ∗ 3 0 + 3 0
4 < 8 6 − 2 1 6 8 0
− 8 2 < − 2 1 6 8 0
4 1 > 1 6 8 0
( 4 1 ) 2 > ( 1 6 8 0 ) 2
1 6 8 1 > 1 6 8 0
This is clearly true, so the original statement is true
Sqrt (2) - Sqrt(1) = 0.4+
Sqrt(4) - Sqrt (3) = 0.3-
Sqrt(10) - Sqrt(9) = 0.16+
Therefore, the smaller figures' must be of greater difference.
Yes,this is simplest solotion of the [roblem and I did this way.
Log in to reply
All right.
Log in to reply
Thanks & Congrats!!
You should add that the sqrt function is strictly increasing for any positive number.
Simple. Just consider the value of "√(n+1) - √n" when increase "n", it tends to 0.
we can say that both √8-√7 and √6-√5 are positive then, let √8-√7=x ⇒8+7-2√56=x²⇒15-√224=x².........[1] again let √6-√5=y ⇒6+5-2√30=y²⇒11-√120=y²..........[2] then from [1]and[2] we can say √224>√120⇔[2]>[1] therefore √6-√5 >√8-√7
d/dx(sqrt{X}) = 1/2sqrt(x). As x increases, slope of curve decreases. Draw 2 lines at x=k and x=k+1 for any k>=0. Draw two lines parallel to x axis which pass thru the intersections of curve with X=k and x=k+1. Let these lines intersect y axis at y1,y2. Let z=y2-y1 (y2>y1). If k increases, you'll find that z decreases. This is due to the nature of the curve that was deduced in the first step. Therefore, (c) is correct.
I did this graphically. The reasoning is that the function is concave down and increasing. When a function is concave down and increasing OR concave up and decreasing, the difference between successive terms decreases as x increases.
The square root function has a decreasing slope. This is easily seen by eye and also by looking at the derivative function.
Therefore, the steps between the value of the function at adjacent X are becoming smaller as X grows with 0 as a limit as X approaches infinity.
The gaps between the two X's are same between the two different answer choices.
Thus the second choice in the list is the right answer, the one with 6 and 5.
well i pictured it this way.. see the more the valve in the root the lesser its numerical value is... take examples of root 4 root 9 and root 16 see the pattern
This solution is similar to Nihar Mahajan's solution.
Another interesting thing about these equations, ie. x − x − 1 is the complex conjugates are also the multiplicative inverse so x − x − 1 = x + x − 1 1 , so we can simply observe 8 + 7 > 6 + 5 , thus 8 + 7 1 = 8 − 7 < 6 − 5 = 6 + 5 1
Observe that for consecutive integers 1 , 2 , 3 , 4 , … , n their squares are increasing at an increasing rate 1 , 4 , 9 , 1 6 , … , n . Since square roots must follow the opposite (i.e. inverse) pattern to squares, observe then that square roots of consecutive numbers increase at a decreasing rate. As an instant of this consequence, 6 − 5 > 8 − 7 .
Rationalize both surds and then it can be clearly seen that sq.root 6 - sq. Root 5 is greater since its denominator comes to be smaller.
Just look at x^1/2 graph ... You can see as the slope goes on decreasing f(6)-f(5) will be greater than f(8)-f(7)
I found using logarithms better and easy.. ie.,
Since all the given numbers, ie \sqrt{8}, \sqrt{7}, \sqrt{6}, \sqrt{5}, are irrational numbers, it is obvious that \sqrt{8}-\sqrt{7} is not equal to \sqrt{6}-\sqrt{5}.
Then, assuming \sqrt{8}-\sqrt{8} to be greater than \sqrt{6}-\sqrt{5}, we have /[ \dfrac{{\sqrt{8}-\sqrt{7}}{ \sqrt{6}-\sqrt{5}} > 1/]
Implying, 0.5 x( ln8 -ln7 -ln6 + ln5 ) < 0...
It is obvious fro the above statement that it is true, since 8>7>6>5 and hence ln8>ln7>ln6>ln5 follows.
Hence ln5 cannot be greater than (ln8 +ln7 +ln6 )..
Hence our assumption is true.
If it would have been false, our assumption would have been false... :)
By taking log it can be easily solved. log(6^1/2-7^1/2)>log(8^1/2-7^1/2)
This was displayed incorrectly. It looked like root 6 minus 1. The whole root 5 wasn't shown.
This is my first written feed back on this site. I may make mistakes and would like some input.
I set up:
8^(1/2) - 7^(1/2) -->
ln(8^(1/2)) - ln(7^(1/2)) -->
(1/2)(ln(8)) -(1/2)(ln(7))-->
(1/2)(ln(8)-ln(7))-->
(1/2)(ln(8/7)-->
I know that if I were to input y=ln(1), y=0. The graph increases ad infinitum afterwards.
I would look at the quotients within the ln(x) and see which ratio is greater.
6/5 > 8/7-->
1.2 >1.14... -->
The ratio between 6:5 is greater and therefore would have a greater difference.
Moderator note:
Congrats on your first solution! Keep on improving :)
It is not clear what you mean by " 8^(1/2) - 7^(1/2) --> ln(8^(1/2)) - ln(7^(1/2)) --> ...."
Are you trying to suggest that 8 − 7 = ln 8 − ln 7 ? If so, that is not correct.
Are you trying to suggest that a > b > 0 ⇒ ln a > ln b ? If so, that is correct. However, it is not true that ln ( 8 − 7 ) = ln 8 − ln 7 .
My goal was to use rules of logs to manipulate the expressions into something I could compare easily. I do not remember if using rules of logs the expression had to be an equation or inequality. As for using the ln(a)>ln(b) expression, what would be the best way to include that into the math flow?
Here is a theoretical approach. We know that 8-7=6-5 because integral numbers grow at a fix rate of 1. But how do these numbers' square root behave? Do they also grow at a fix rate? Considering that: Sqrt (1) = 1 and Sqrt (4) = 2: it takes 3 numbers (from 1 to 4) to its Sqrt grow 1 Sqrt (4) = 2 and Sqrt (9) = 3: it takes 5 numbers (from 4 to 9) to its Sqrt grow 1 So square roots from integer numbers grow at a decreasing rate, not a fix one. Therefore the difference between two consecutive bigger numbers’ square roots ( Sqrt(8) – Sqrt (7) ) will be smaller than the difference between two consecutive smaller numbers’( Sqrt(6) – Sqrt (5) )
Considering the question, We imagine (^4 - ^3) and ( ^2 - ^ 1),we find that ( ^ 2 -^ 1) is bigger. on same lines we find (^6 - ^5) is bigger tha ( ^ 8 - ^ 7)
Simple, just becouse of the rational fuction tendency. When greater the number smaller is his growth
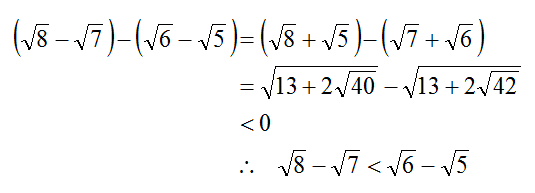
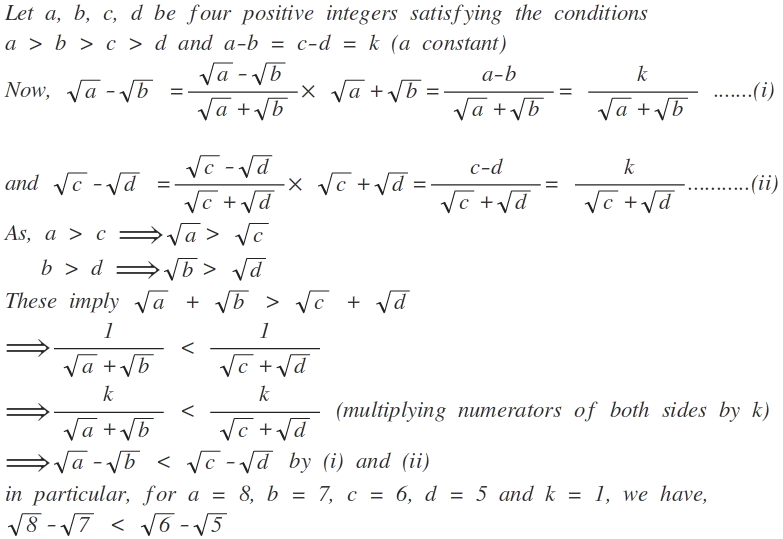
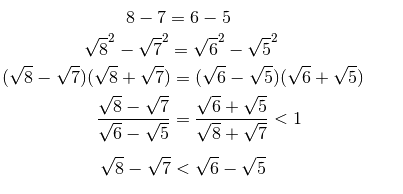
8 − 7 = 8 + 7 ( 8 − 7 ) ( 8 + 7 ) = 8 + 7 ( 8 ) 2 − ( 7 ) 2 = 8 + 7 8 − 7 = 8 + 7 1
6 − 5 = 6 + 5 ( 6 − 5 ) ( 6 + 5 ) = 6 + 5 ( 6 ) 2 − ( 5 ) 2 = 6 + 5 6 − 5 = 6 + 5 1
We certainly have:
8 + 7 > 6 + 5 ⟺ 8 + 7 1 < 6 + 5 1 ⟺ 8 − 7 < 6 − 5
Thus 6 − 5 is greater.