Complete Circle Packing
Is it possible to place (infinitely many) closed discs (of positive radius) in a unit square, where the interiors of the discs do not intersect, such that any point given in the interior of the square lies on a disc?
- The interior of each disc must be contained in the unit square. The perimeter of the disc can touch the perimeter of the square.
- The interiors of 2 discs do not intersect. The perimeters of the discs are allowed to intersect (so they touch each other).
- Note that the corners of the square cannot be covered by a closed disc, which is why I'm asking about the interior.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Michael Mendrin @Brian Charlesworth @Arjen Vreugdenhil Alright, I think this constitutes a proper proof. Thoughts? Can I definitively update the answer to no?
Log in to reply
If had to answer I would say: Very nice and beautiful. Congratulations!
Love the proof! "No" wins the day, definitively.
There you have it. I was thinking along the same lines but never made the jump to intersection with arbitrary lines. Good thinking!
Do we intend to cover the side? The side is in the boundary, not the interior
Log in to reply
The interior is defined as any point in set S that is not on the boundary. So since we're only concerned about the interior of the square, we do not intend to cover the side.
Note that (as mentioned in the solution), it is impossible to cover the side with countably many circles.
"@Arjen Vreugdenhil – Because the rational points are a set of measure 0, and you are giving up control over the radius, I can cover the rational points by discs of total area < 1 (actually close to 0), which shows that this approach will not work."
Showing that a cover fails is not a proof that any cover would fail.
Log in to reply
Yes. The comment wasn't a proof that "any cover would fail".
The comment indicated that "Arjen's approach doesn't show that the answer is Yes. His cover fails for the following reasons ...". Once again, let me reiterate that I don't know what the correct answer definitely is.
No matter how small of a circle you make, it'll still leave a gap in the corner.
Log in to reply
Good thought! Let's develop that idea further. We can show that the area of that gap goes to 0, so how do we know that there is a point which can never be filled?
Also, what if we never ever really had a corner? We just use many circles that "nearly touch" each other, but might not be exactly tangential.
Not sure if this is helpful, but here's something that I thought :
We consider order the set of all collections of (disjoint) balls contained in the unit square by set inclusion. Then, if { B n } n ∈ N maximal collection (which exist by Zorn's lemma) then ( ∪ n ∈ N B n ) c has empty interior. Here, complements are with respect to the unit square.
"The interval cannot be expressed as the disjoint union of countably many closed intervals (possibly of 0 length)."
This statement represents a significant change to the problem. There is nothing in the original statement of the problem that requires the discs to be disjoint.
It is trivial to represent the interior of (0,1) as a countable union of closed intervals, whose
interiors
are disjoint.
Log in to reply
Please read carefully. I am not applying that theorem directly.
I am applying that theorem (with work) in the lemma to conclude that "Any line through the square has to pass through a tangency point of 2 discs". In particular, as you read the proof of the lemma, I am arguing that "It's not possible for the circles to all disjoint (which is the all almost kissing case). Some of them have got to be actually touch".
We can thus count those "points of tangency", where the "closed intervals touch", and deriving a contradiction from there.
Log in to reply
Thanks for identifying that edge case.
I've cleaned up the presentation and made it explicit what I intend to do, to avoid others jumping to conclusions about how these steps will be done.
Let me know if things are still unclear.
The comment said "this approach will not work"' but the comment did not show that. It showed that the approach
might
not work. I'm hard-pressed to see how to fix it, but proving either side of this proposition seems difficult.
I suspect that no proof in either direction will be found. The framing of the question is to take the countable union of disjoint closed sets, but we don't know anything about the countable union of disjoint closed sets (except that the measure of the union is the sum of the measures of the individual sets). While it is easy to create a collection of closed sets with total measure < 1, that fact doesn't imply that it isn't also possible to create a collection of disjoint closed sets with total measure = 1. Of course having total measure 1 would only be a necessary and not sufficient condition for the union to be able to cover the entire interior of the unit square.
Log in to reply
Simply looking at "countable union of disjoint closed sets" is not sufficiently strong enough to approach this question. For example, we can cover any region (under suitable conditions) with infinitely many squares, using the naive / greedy algorithm approach of taking squares which work else cutting them up into 4's each time.
Ultimately, I think that the crucial part is that these circular regions are only allowed to intersect at 1 point on the boundary. I think that the proof would be similar to the Serpenski triangle argument that I had, but generalized to allowing for finitely many regions during each iteration (instead of always 3 each time).
The difference with "using squares to cover a region" is that the squares which we had were intersecting on an entire side / infinitely many points, whereas the circles can only intersect at one point.
Note: This argument will miss the case where circles are not forced to touch each other, which I've not given serious thought to (other than what a pain it would be to deal with them).
Let's suppose that we can place infinitely many closed discs of positive radius in a unit square where the interiors of the discs do not intersect, such that any point given in the interior of the square lies on a disc, then we can take(choose) (assuming axiom of choice) one countable number of points (a sequence of different a n formed by the centers of some different circles of radius r n > 0 ) inside of some of these closed circles. Then, due to Weierstrass theorem, this sequence must have a subsequence a n k converging to a point A in the clousure of the square, but closed discs of positive radius do not intersect, i. e, the radius r n k of these circles containing a n k is decreasing to a limit 0. This leads to a contradiction: Sketch of proof: Take a closed disk of radius ϵ > 0 around A , that is, D ( A , ϵ ) , ... Following this process, k 1 , k 2 → ∞ lim d ( a n k 1 , a n k 2 ) = 0 ≥ k 1 , k 2 → ∞ lim r n k 1 + r n k 2 , and this leads to circles with limit of radius being equal to 0... For visualizing my idea think about three mutual tangent circles, then to cover the space between these circles with circles, in some moment we should use circles of radius 0.
Topologycal proof.-
Let's call A be the interior of the unitary square and Cl (A) = A ∪ { sides of this square } , and let's suppose that A can be covered by B = ∪ { countable infinitum closed circles such that... } then, A ⊂ B ⊂ C l ( A ) ⇒ B is a connected set. And, Cl (A) ⊆ Cl (B) ⊆ Cl (Cl (A)) = Cl(A) ⇒ Cl (A) = Cl (B) and Int (A) = A ⊆ Int(B) . Let's take now C = ∪ { countable infinitum open circles with the same radius as the circles in B } . Then, C is contained strictly in A ,because C is an open set and if A was equal to C , A wouldn't be a connected set, however C ⊂ A ⊂ B ⊂ Cl (C) ⇒ Cl(B) = Cl (C) . Conclusion, C , A are open sets, with C contained strictly in A with Cl(A) = Cl (C) ⇒ int(Cl(A)) = A = Int(Cl (C)) = Int(C ∪ Boundary(C) ) = C (Contradiction)
Question.- If C is an open set, then , Int(Cl(C)) = C ? No, it's not true, Int(Cl(U)) = U being U an open set, nevertheless C is the union of disjoint open circles with positive radii, then it's clear that Int(Cl(C)) ⊃ C because Int(Cl(C)) is the greatest open set contained in Cl(C)) . Let's suppose that Int(Cl(C)) = C then would be a point a ∈ Int(Cl(C)) = A ⊂ B such that a ∈ / C , then due to Int(Cl(C)) is an open set, for all neighborhood N ⊂ A around a ∈ A , we have two possibilities:
a) N ∩ C = ∅ . This scenario is impossible because if it was true B wouldn't cover A and we are supposing that B covers A .
b) N ∩ C = ∅ . This leads also a contradiction because then a ∈ Cl(C)) and then Cl(C)) = Int(Cl(C)) and this would imply that R 2 is not a connected set.
Therefore, Int(Cl(C)) = C .
Log in to reply
Great to see that others are thinking of topological arguments. I've been playing around with these centers (or a representative point in each circle) and their accumulation points too. It does seem like one of these accumulation points will fail to be in a disc.
Unfortunately, there is an error at the end of your argument. It is possible for an accumulation point to be valid for the following reasons:
-
I agree that the limit point seems unlikely to be in any of the discs of the subsequence. However, since this is a subsequence, we have to consider the case that the limit point is a disc that is not part of this subsequence. As an explicit example, suppose we had a circle of diameter 1/2 on the left, and then circles of diameter 1 / 2 n + 1 on the right. The limit of the circles on the right lies on the circle on the left.
-
The limit point exists in the closure of the set, so it could be the perimeter of the square which isn't included. (Minor concern since we can deal with this by choosing a sequence that is contained in a region that doesn't touch the perimeter)
It is not clear to me how this argument could be tweaked to get the desired result.
You can get closer and closer to the corner, as the radius of the circle approaches 0, but you can never get there.
Log in to reply
Note that we're excluding the boundary of the square, which is why the question is phrased as "point in the interior of the square".
If you're referring to a region cut out by the circles, then these points are already in the original discs, hence the "corner" is included.
I'm not posting anything rigorous because I'm not that adept at this. I'm just stating why I think the answer should be NO.
I'm assuming it's not possible to cover the sides with countably infinite circles. Now, let's think there's a circle (I'm calling it the first circle) in the middle of the square. We've to assemble other circles around it. With every step there will be space left behind. So, we will be zooming into the perimeter of the first circle and trying to cover up the non-occupied space (for an infinite amount of time).
As we're zooming (infinitely) into the perimeter of the first circle, it eventually becomes (or, tends to) a straight line. But, we've already assumed that we cannot cover the sides of the unit square which is essentially a straight line. Hence, we can either prove we can cover every single space within the square (including the corners and sides) or we cannot.
Log in to reply
Unfortunately, when you're zooming onto the perimeter of the circle, those points on the perimeter are already covered by the circle. So yes, the remaining circles will only touch the perimeter at countably many points, but this doesn't imply that all of the space cannot be filled in.
Let's suppose that we can place (infinitely many) closed discs (of positive radius) in a unit square, where the interiors of the discs do not intersect, such that any point given in the interior of the square lies on a disc. Due to your observation 1: there are countably many circles... Let's call them, { B n } n ∈ N , these closed bounded balls covering the interior of the square, they are compact sets. Due to observation 2, the side of the square can't be covered by these circles. Take x in the side of the square such that x doesn't belong to ∪ n ∈ N B n . For example , take x being a corner of the square. For each, n ∈ N let's define d ( x , − ) : B n ⟶ R , ∀ y ∈ B n , d ( x , y ) = euclidean distance from x to y . Being B n (n is a fixed natural number) a compact set and ∣ d ( x , z ) − d ( x , y ) ∣ ≤ d ( z , y ) (triangular inequality), d ( x , − ) is a continuous function of a compact set in R which it is bounded, then due to Weierstrass- theorem, this function has a maximum and a minimum. Obviously, this minimum is greater than 0 , because if the minimum of this function was 0 , x would belong to B n . (Contradiction). minimum d(x, B n ) = d ( x , y n ) being y n the point in the boundary of B n joining x with the center of B n .
Nevertheless, d ( x , ∪ B n ) = infimum { d ( x , y ) , such that y ∈ ∪ B n } = 0 , i.e, ∃ r n ∈ ∪ B n such that n → ∞ lim d ( x , r n ) = 0 = d ( x , n → ∞ lim r n ) , because the function d ( x , − ) is a continuous function ,and this implies n → ∞ lim r n = x .
On the other hand, d ( x , Int(B n ) ) = d ( x , y n ) , ∀ n ∈ N , such that n is a fixed natural number althought y n ∈ / Int(B n ) ⇒ d ( x , ∪ Int(B n ) ) = infimum { d ( x , y ) , such that y ∈ ∪ Int(B n ) ) } = 0 , i.e, WLOG ∃ ( a n ) ∈ ∪ Int(B n ) such that n → ∞ lim d ( x , a n ) = 0 = d ( x , n → ∞ lim a n ) , because the function d ( x , − ) is a continuous function ,and this implies n → ∞ lim a n = x Let's call D = ∪ B n , A = interior the unitary square and Cl(A) = A ∪ sides of the square then we have A is a connected set and A ⊂ D ⊂ Cl(A) ⇒ D is a connected set. The continuous image of a connected set is a connected set. Hence d ( x , − ) ( ( D ) ) = d ( x , ∪ B n ) = ∪ d ( x , B n ) is a bounded interval (non empty) in R containig at least two different points...
proof:
the convergence a n → x prove that x ∈ Cl( ∪ Int(B n ) ) , and x ∈ Cl( ∪ Int(B n ) ) ⊃ ∪ (Cl(Int( B n ) ) ) = ∪ B n and x ∈ / ∪ B n . I'm going to prove :
Cl( ∪ Int(B n ) ) = ∪ B n .
One inclusion is proved,if a ∈ Cl( ∪ Int(B n ) ) , then for all "very, very small" open neighborhood N around a , N ∩ ( ∪ Int(B n ) ) = ∪ ( N ∩ Int(B n ) ) = ∅ , ∪ Int(B n ) ) is the union disjoint of open sets, this implies that a ∈ ∪ B m . (See below note). Therefore, we have proved the above equality, and this implies that x ∈ ∪ B n and x ∈ / ∪ B n (contradiction).
Note.- If A ⊂ B , then Cl(A) ⊂ Cl(B) .
N ∩ ( ∪ Int(B n ) ) = ∪ ( N ∩ Int(B n ) ) ⊂ ∪ B n
Question.- ∪ Int(B n ) ) ⊂ Int( ∪ B n ) = ∪ Int(B n ) ) ? . No. What is the interior of a countable number of closed, bounded balls in R 2 with positive radius and intersection among two of them being at most a point?
R 2 is a Baire space, and all points of intersection ( d n ) of each two closed balls of ∪ B n have empty interior, ie, the countable union ( ∪ d n ) of all these intersecting points of the closed balls has an empty interior. This says us: ∪ Int(B n ) ) = ∪ Int(B n ) ∪ Int( ∪ d n ) ⊂ Int( ∪ B n ∪ d n ) = Int( ∪ B n ) .
"Guide for another possible proof"".-
There can only be 1 closed "disjoint" ball with a radius of 1/2 in the square, and there is space in the interior of square not covered
There can only be 4 closed "disjoint" balls with a radius of 1/4 in the square, and there is space in the interior of square not covered.
There can only be 16 closed "disjoint" balls with a radius of 1/8, and there is space in the interior of square not covered.
There can only be 64 closed "disjoint" balls with a radius of 1/16, and there is space in the interior of square not covered.
There can only be 256 closed "disjoint" balls with a radius of 1/32, and there is space in the interior of square not covered.
There can only be 4 n − 1 closed "disjoint" balls with a radius of 2 n 1 , and there is space in the interiror of square not covered. As n → ∞ , if the space in the interior of the square could be covered with a infinitum countable number of closed "disjoint" balls with positive radius, and the sequence 2 n 1 tend to 0 , and 4 ∣ N ∣ is an uncountable number...
"Guide for another possible proof.-" G
Every sequence bounded in R has a convergent subsequence. Consider to be r n the radius of the closed and bounded ball B n . This sequence r n is bounded in R , WLOG, let r n be the subsequence converging. Obviously r n has to coverge to 0 . Then, for example, for ϵ k = 1 0 0 0 0 1 0 0 0 1 0 0 0 0 k 1 , k ∈ Z + , there exist an infinitum countable number of radius r n k smaller than ϵ k and only a finitum number of radius r n k bigger than ϵ k . Then we can choose radii, WLOG, r n , being r 1 the greatest radius, r 2 < r 1 the next greatest radius,i.e, we can stablish a well- order about the radii,i. e, … < r n < r n − 1 < … < r 2 < r 1 . Now we choose the centers c n of these closed balls of radius r n . The sequence c n is a bounded sequence and this implies, there exists, WLOG, a subsequence c n converging. Where can this subsequence c n converge if the radii are positive?...
another proof.-
Since ∪ B n ) only can have a countable number of points in a side of square, and the side of square has an uncountable number of points and it's a point of adherence(clousure) of the interior of square, then is a point of the clousure of ∪ B n ) . But around of this point belonging to the side of square which it is not a point of ∪ B n ) lead us this union can't be a countable union...
"Another possible proof.-" R 2 is a Baire space.
Lemma.- Every open set in a Baire space is a Baire space.
Theorem.- X is a Baire space if and only if given any numberable family { U n } of open sets in X , each of which is dense in X , its intersection is also a dense set in X.
Lemma.- If C 1 ⊃ C 2 ⊃ … is a sequence of closed non-empty sets, in a complete metric space X, (this implies that X is a Baire space), and diameter (C n ) → 0 then ∩ C n = ∅ .
Then, using G this leads us a other contradiction, do you know how?..
Log in to reply
If I understand you correctly, you construct a sequence r n on the boundaries of the discs, and a sequence a n in the interiors of the discs. Both converge to x . This construction seems valid.
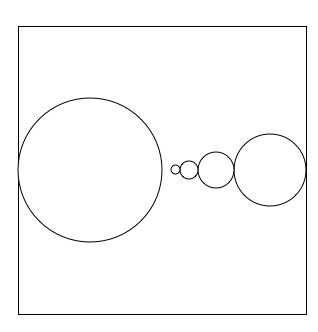
But your claim that "then x would be a tangential point for some B n " is essentially the claim that ( 1 ) x ∈ ∪ Cl ( B n ) = ∪ B n , but that does not follow. The convergence a n → x only proves that ( 2 ) x ∈ Cl ( ∪ B n ) , which is very different. To conclude that (2) implies (1) is tantamount to saying Cl ( ∪ X n ) ⊂ ∪ Cl X n , which is known not to be valid in general.
A counterexample is suggested by the following drawing:
If we work with closed discs, point
P
will lie in the closure of their union, but not in the union of the (closures of) the discs.
Log in to reply
the convergence a n → x prove that x ∈ Cl( ∪ Int(B n ) ) and r n → x prove that x ∈ Cl( ∪ B n ) and x ∈ / ∪ B n . Therefore, x ∈ Cl( ∪ Int(B n ) ) ⊃ ∪ (Cl(Int( B n ) ) ) = ∪ B n and x ∈ / ∪ B n , can you see the contradiction?... Forget, x is in the perimeter..
Log in to reply
@Guillermo Templado – How is that a contradiction?
- I agree that x ∈ C l ( ∪ I n t ( B n ) ) . (Let's call this T)
- I agree that ∪ ( C l ( I n t ( B n ) ) is a subset of C l ( ∪ I n t ( B n ) ) (Let's call this S)
- I agree that x ∈ ∪ B n .
Given that x is an element of T , and that S is a subset of T , how do we conclude that x must be a point in S ? Why can't x be a point in T − S ?
In the counter examples that have been stated, we're showing you how x is a point in T − S . Please look at these counter examples. If you think that they are not valid, point out what the error is.
Log in to reply
@Calvin Lin – ok, I'm going to look those counterexamples, righ away... And I'll tell you what I think... but think about this, I this problem is similar to this question? Take S = ∪ n = 1 ∞ [ 2 n 1 , 2 n + 1 1 ] Then, 0 ∈ / S . But, then why 0 ∈ Cl(S) = S ? because precisely, the limit of the distance of these intervals is 0. And this happens here, i.e, if you want to fill the interior of unitary square with closed balls you need points.... Why?, there is an example above, how can you fill with a corner with positive closed balls?... Ok, I'm going to see your examples...
Log in to reply
@Guillermo Templado – What you have is a great example! The closure of the union (T) is not necessarily equal to the union of the closure (S) - the point 0 is in T but not S. That's what I've been trying to get across.
As such, going back to the thread of your argument, we are not able to conclude (for certain) that x ∈ B n , and hence there is no contradiction.
(Yes, for this to occur, we will need that the radius of the discs tends to 0. Let me preemptively remind us that there is no minimum of the radius, and that their infimum is 0)
I'm not sure what the rest of your comment is about. That seems to be a completely new direction. If so, I have to ask you to be more explicit in stating what you are saying, because there are too many blanks which I am unable to fil in. Here are some of my concerns / doubts about your phrasing. The more clarity that you can provide, the better I can understand what you are trying to say.
-
I'm not sure what you are trying to convey. Can you be explicit and state what you want to achieve? E.g. "I want to prove by contradiction, by showing that both x ∈ B n and x ∈ B n . I will do it by these 5 steps", or the tldr that I gave at the start of my edited solution to provide clarity about how the argument proceed.
-
I'm not sure what "you need points" you refer to. If you are referring to the point x in your argument, then recall that you chose it to be on the perimeter, which we do not care about.
-
It seems to me that you are no longer forcing "you need points" to be on the perimeter. This comment will relax that and refer to x being a point in the interior and we want to show that it's not covered. In which case, even though x ∈ T and S ⊂ T , we do know for certain that x ∈ T − S . All that we know is either x ∈ S or x ∈ T − S . Furthermore, even if x ∈ T − S , it could be possible that x is covered by another circle.
-
I'm not sure what you mean by "how can you fill ...". In fact, given this solution, the answer is we cannot fill no matter what. The goal is to prove this directly, instead of claiming that this cannot be done because the reader cannot come up with an approach
-
Yes, any closed, non-overlapping cover of the unit square will have points that are uncovered (and in fact, uncountably many). The goal is to prove this.
-
Focusing on the corner, and in particular the line y = x , there is a closed, non-overlapping cover of the square, which ensures that { ( r , r ) ∣ 0 < r < 1 } is completely covered, while the point ( 0 , 0 ) is not covered (and in fact cannot be covered by any disc of positive radius). We simply take "maximal discs along the diagonal".
Log in to reply
@Calvin Lin – 1.- take all the points in a side of square and make the same process.
2.-I'm not sure what "we need points" either....
3.-You can take x the only point of tangency of two circles.
4.- how can fill with circles of positive radius the points closest to one corner . tangent at most to sides of the square? "No matter how small of a circle you make, it'll still leave a gap in the corner." (Michael Coley)
5.- Yes, think of the perimeter of a circle what has an uncountable number of points, if there exists such cover.... This is the goal and
6.- Exact, very good idea, it can a key to a solution...
Log in to reply
@Guillermo Templado – Sorry, I still have no idea what you are trying to convey. My best guess is "Here are some thoughts which might lead to a possible solution", as opposed to "Here is how my (original) argument continues".
2+3) When I was referring to "you need points", I was referring to your phrase in "if you want to fill the interior of unitary square with closed balls you need points....". I'm not sure if those points were meant to be the same as the points x .
4) That is a circular argument. You are saying that right now I see no way to fill it, hence there is no possible way to fill it. Note also that "Yes, we cannot fill it with finitely many discs. But how do we know that we cannot use (countably) infintiely many discs and fill it?"
For example, in the related question of covering the unit circle with squares, then "no matter how small of a square you make, it'll still leave a gap in the perimeter". Yes, there is no finite cover that will cover the disc. However, there does exist an infinite cover that covers the disc.
(Minor note: This is what I was referring to by transfinite induction. We can prove the finite case by induction, but we cannot prove the "limiting / infinite" case. There is (generally) non-trivial work to be done)
5+6) Those statements turn out to be true. The question is, why are they true? What is the proof that indicates they are true?
Log in to reply
@Calvin Lin – I have changed my previous proof, Calvin, what do you think,please? I know you are going to think, but d ( x , A = 0) and A is the union of points, which they are compact sets.... d ( x , A = 0) because x is a point of tangency of A and we are assuming that x is not a point of tangency of D ...
@Calvin Lin – Yes, effectively Calvin, if you want to cover the interior of the square you'll need points. Why? Think about a corner of the square in the boundary of the interior of the square, then using the last below lemma you'll need points, and you can't cover the interior of square with closed "disjoints" circles with positive radius. Use lemma 1, you'll need points and furthemore this lemma implies that you'll need an uncountable number of points. Can you prove it? or can you see why?
R 2 is a Baire space.
Lemma.- Every open set in a Baire space is a Baire space.
Lemma 1.- If C 1 ⊃ C 2 ⊃ … is a sequence of closed non-empty sets, in a complete metric space X, (this implies that X is a Baire space), and diameter (C n ) → 0 then ∩ C n = ∅ .
Log in to reply
@Guillermo Templado – Of course, this lemma is assuming Zorn's Lemma... This problem is similar to this question, Does there exists a number between the cardinality of N and the cardinality of R ? the answer is yes and no... Of course, how is this lemma possible if the interval (0, 1) is a Baire space and the closed sets A n = ( 0 , 2 n 1 ] ⊂ ( 0 , 1 ) is a sequence of closed non- empty sets in (0,1) in a complete metric space ( [0,1] ). and diameter(A n ) → 0 and then, what is ∩ A n ?...
Log in to reply
@Guillermo Templado – The intersection ⋂ n = 0 ∞ ⟨ 0 , 2 n 1 ] = ∅ .
Lemma 1 does not apply here because ⟨ 0 , 1 ⟩ with the Euclidean metric is not a complete metric space.
Proof: the sequence ( n 1 ) n = 1 ∞ is a Cauchy sequence in ⟨ 0 , 1 ⟩ but its limit 0 ∈ ⟨ 0 , 1 ⟩ .
Log in to reply
@Arjen Vreugdenhil – Yup, it was typo, but the idea for proving the solution is there.. we can stablish an order from the radii r n from the closed balls B n from the greatest radius to the infimum radius of lenght 0, obviously the radii don't have a minimum... Take a corner... Ok, give me one day, please..
Log in to reply
@Guillermo Templado – i.e, we can find positive radii r 1 > r 2 > r 3 > . . . from closed "disjoint" balls B 1 , B 2 , B 3 , . . which distance to a corner x will always be greater than 0 and, furthemore, we choose these closed balls the closest possible to x , because the radii are positive, and we can create the following closed non-empty sets C 1 = [ 0 , r 1 ] ⊃ C 2 = [ 0 , r 2 ] ⊃ . . . in the complete, compact metric space [0, 1] with the euclidean metric. Obviously, ∩ C n = 0 because r n → 0 , but we can be closer and closer to the corner x with this balls, but none of these balls will contain x and then its distance to the corner is bigger than any r n and there must always be a space near the corner that we can not cover, and this implies that ∩ C n = ⟨ 0 , a ⟩ ? . This is more or less my idea... I'll try to formalize it... One day, please...
Log in to reply
@Guillermo Templado – Let's suppose that we can place (infinitely many) closed discs (of positive radius) in a unit square, where the interiors of the discs do not intersect, such that any point given in the interior of the square lies on a disc. Due to Calvin's observation 1: there must be countably many circles... Let's call { B n } n ∈ N to these closed bounded balls covering the interior of the square, they are compact sets. Due to Calvin's observation 2, the side of the square can't be covered by these circles. Take x in the side of the square such that x doesn't belong to ∪ n ∈ N B n . For example , take A being a corner of the square.
Now, let r n > 0 (such that n ∈ N ) be the radius of the closed, compact ball B n (each one of these closed, compact "disjoint" balls has a positive radius), and let c n be the center of the closed compact, ball B n . Since r n → 0 as n → ∞ , (it seems obvious but, Why?, because
1.- we can't cover the interior of this square with a finite number of closed "disjoint" balls with positive radius 2.- since r n have a subsequence r n k converging to a number l ( Bolzano Weierstrass theorem ), l has to be 0, because if l was greater than 0 , then there would be an infinitum countable number of closed "disjoint" balls with radius greater than ϵ > 0 inside of the clousure of the square. This is a contradiction,i.e, all subsequences of r n converge to 0 and this implies that r n → 0 as n → ∞ .) (Ican prove that in R n a sequence m n converges to a ⟺ all subsequence of m n converges to a .)
Therefore, since r n → 0 as n → ∞ , we can stablish a well-ordering with the radii of these balls, being r 1 ≥ r 2 ≥ r 3 ≥ . . .
Let's define, fixed a point x ∈ R 2 , d ( x , y ) = eucliden distance from x to y in R 2 , which is a continuous function, becuase of triangular inequality.
Now, let C 1 = [ 0 , d ( A , c 1 ) ] be a compact interval in R with the euclidean metric, that is, remember that A is a corner in the clousure of the square, A is in a side of the square, A ∈ / B 1 because the radius are positive and d ( A , c 1 ) = r 1 + ϵ 1 being ϵ 1 > 0 because A ∈ / B 1 , this implies that d ( A , c 1 ) > 0 ⇒ C 1 is a compact non-empty interval and this interval has more of two points.
Now, let C 2 = [ 0 , d ( A , c 2 ) ] . In the same way and with same reasoning C 2 is a compact interval having more of two points. Then, the crucial question: What is ∩ n = 1 ∞ C n ? { 0 } ⊆ ∩ n = 1 ∞ C n and the intersection of closed sets is a closed set, therefore G = ∩ n = 1 ∞ C n is a closed bounded set (we are supposing the euclidean metric) ,i.e, it's a compact set. If G would have another point b > 0 , then ∀ n ∈ N , d ( A , c n ) = r n + ϵ n ≥ b > 0 and this would imply ∪ B n couldn't cover the interior of the square,since r n → 0 as n → ∞ and ϵ n must tend to 0 obligatory, because if ϵ n didn't tend to 0, A wouldn't belong to Cl( ∪ B n ) = Clousure of the square. So, { 0 } = ∩ n = 1 ∞ C n and this implies that ∃ c n k subsequence of c n such that d ( A , c n k ) → 0 as k → ∞ ,i.e, k → ∞ lim d ( A , c n k ) = 0 = d ( A , k → ∞ lim c n k ) ⇒ k → ∞ lim c n k = A Contradiction . Why? because d ( A , c n k ) = d ( A , B n k ) + r n k ≥ d ( A , B n k ) > 0 and lim k → ∞ c n k = A ⇒ B n k → A and here is the contradiction, because all balls has positive radius. q.e.d
Unfortunately, this argument doesn't work.
Here is my reading of what you're doing (and correct me if it is wrong).
- Given any cover, find a point x on the perimeter that isn't covered. (In fact, we can take x as the lower left corner).
- For each circle B n , let y n ∈ B n be the point that is closest to x . (In fact, y n lies on the boundary of B n and the line segment connecting x to the center of B n )
- Find a subsequence such that d ( x , y i ) → 0 (You used the notation a n , but we can set a n = y n , so let's keep things simple.).
- lim y i = x .
- Conclude that x must lie on some B n , which is a contradiction.
While I agree with steps 1 to 4, I disagree with the conclusion in 5. You are essentially wanting to perform transfinite induction, but that doesn't hold for this property. As an explicit counter example, we can take x as the lower left corner, and then we "maximially fill the diagonal with circles". This gives us a sequence of circles that tend towards the lower left corner (and hence the y n ), but it's obvious that x is never on any circle.
Note: This is one of the potential issues of "almost kissing circles". We do not know anything about the point x , in part because we are forced to choose the subsequence, which loses some information.
Log in to reply
I'm supposing that one cover exists...
1.- Take a point x different to lower left corner, or every corner. 2.- No, y n can be different to the closest ... 3.- no, y n = a n I get a contradiction, I'm not using induction ... What step is not clear for you?
Log in to reply
@Guillermo Templado – Sure
- Suppose such a cover exists. Find a non-corner x on the perimeter that isn't covered.
- For each circle, define an interior point a n
- Find a subsequence such that d ( x , a i ) → 0 .
- lim a i = x
- Conclude that x must lie on some B n .
Is that what you are doing?
Log in to reply
@Calvin Lin – Yes, less point 5, x must to be in the perimeter for some B_n
Log in to reply
@Guillermo Templado – Alright, as before, I disagree with the conclusion. (Forget what I said about wanting to perform induction on the property of inclusion). Note that the countable union of closed sets need not be closed, which is why even though a i is in ∪ B n , we cannot conclude (yet) that their limit point is also in ∪ B n .
As an explicit counter example, suppose that the open cover contains the circles with center ( 2 n 1 , 2 1 ) and radius 2 n + 1 1 . These circles are disjoint (and in fact do not intersect). Then, take the subsequence of points a n = ( 2 n 1 , 2 1 ) . It is clear that their limit is x = ( 0 , 2 1 ) , which doesn't lie in any of these circles.
Log in to reply
@Calvin Lin – Let's suppose that the there exist a cover... and D = ∪ B n . I'm taking a point x in the side of the square... Then, D is not a closed set, and it's an open set,why? Let A be the interior of the square, A ⊂ D ⊂ Cl(A) . The previous inclusions are strict because D is not an open set because of D has to have at least one point in the boundary of A , because if D doesn't have any point in the Boundary of A , then B can't cover A , because A is an open set and all points in A have a neighborhood contained in A . In fact, B has to have a countable infinitum number of points in all the sides of Cl(A) and D can't be a closed set because Cl(A) is the smallest closed set containing A and A ⊂ B ⊂ Cl(A) ... Ok, I finish here... A suggestion: read again "my proof"
Log in to reply
@Guillermo Templado – If B n is a cover, then D = ∪ B n is equal to the entire space, which is trivially both open and closed.
@Guillermo Templado – I am trying to read your proof. There is clearly something that I'm not getting from what you are trying to express.
Can you explain how we "Conclude that x must lie on some B n "? The part which I think you show it is
(Contradiction, because then x would be a tangential point for some B n , since ∪ Int(B n ) ⊂ int( ∪ B n ) is contained in the interior of the unitary square).
I agree that "the union of the interiors" is a subset of the interior of the union. But, how does that explain that x must lie on some B n ? Please be explicit about what you're doing. I would appreciate if you used the B n as I described above, namely circles with center ( 2 n 1 , 2 1 ) and radius 2 n + 1 1 , and explain which B n the point ( 0 , 2 1 ) would lie in by your proof.
Log in to reply
@Calvin Lin – Yes, the contradiction is because the sequence a n is in the interior of the square and due to lim n → ∞ a n = x and x is in the side of the square and we are supposing that x ∈ / ∪ B n , since a n ∈ ∪ Int(B n ) then x is a point of acumulation of the sequence a n ,and x is a point of acumulation of ∪ B n = ∪ Cl(Int(B n ) ) so x has to be in the perimeter of some B n .
Log in to reply
@Guillermo Templado – Let me breakdown what you're saying, and whether I agree with it or not.
- the sequence a n is in the interior of the square - I agree that the sequence of points is in the interior.
- and due to lim n → ∞ a n = x - I agree that x is the limit of this sequence
- and x is in the side of the square - I agree this is the choice of x
- and we are supposing that x ∈ / ∪ B n , - I agree this is the choice of x
- since a n ∈ ∪ Int(B n ) then x is a point of acumulation of the sequence a n , - I agree
- and x is a point of acumulation of ∪ B n - I agree that x is an acculumation point of ∪ B n .
- ∪ B n = ∪ C l ( I n t B n ) - I agree with this, since B n = C l ( I n t B n ) .
- so x has to be in the perimeter of some B n . - I diagree with this. (Once again, correct me if I misinterpret you) I think that you are claiming that "the closure of a union is equal to the union of the closure, meaning that C l ( ∪ B n ) = ∪ C l ( B n ) . Hence x ∈ C l ( ∪ B n ) = ∪ C l ( B n ) ⇒ x ∈ C l ( B n ) for some n ". Unfortunately, the first claim about the equivalance of the closure of sets is not true. As an example, use the B n as I described above, namely circles with center ( 2 n 1 , 2 1 ) and radius 2 n + 1 1 , and points a n = ( 2 n 1 , 2 1 ) . The accumulation point ( 0 , 2 1 ) is not in any of the balls.
I have requested that you use this explicit balls to explain your argument. Please, for my sake, explain how these balls work in your argument, or tell me which condition these balls do not satisfy.
From 6, we have x is an accumulation point of ∪ B n , and thus x ∈ C l ( ∪ B n ) . Note that C l ( ∪ B n ) = ∪ ( C l B n ) . It is not always true that "the closure of a union of sets is equal to the union of the closure of sets". (Though, these are equivalent if we're only taking finitely many sets.) I will admit that topological equivalences like this can be tricky to determine, and we have to be careful that the steps of the proof are indeed valid.
After all of this, I'm simply restating the same thing multiple times. I see that i'm not getting through to you and explaining that "We cannot conclude that x must lie on some B n ", because you do not review my counter example, and simply stated that it has to be true without proof.
@Calvin Lin – ok, my thought about this is exactly what I have said in my proof and my last comment. I think we are going on circles. We need a break, to meditate, at least 3 or 4 days... I think
The biggest reason why your proofs would not work, is that it doesn't distinguish between the "cover circle with squares" vs "cover square with circles". The former can be done, but the latter cannot be done (or so we claim). If you run through your proof in the "cover circle with squares" case, you can start to see where the issues are.
Furthermore, use the examples that we've listed out to test the validity of your proofs. We've given several "almost kissing discs" configurations, in which the limit point is never in the union. What is it about your proof that would force the limit point to be in the union (when it clearly is not)?
The main place where I disagree with your argument, is in saying that
The continuous image of a connected set is a connected set. Hence d ( x , − ) ( ( D ) ) = d ( x , ∪ B n ) = ∪ d ( x , B n ) is an interval in R containig the point 0
Why must the interval contain the point 0? The set d ( x , 0 ) ( D ) is going to be of the form ( 0 , 1 + ) . In order for 0 ∈ d ( x , 0 ) ( D ) , we must have x ∈ D , for which you have offered no proof. (And in fact, by construction, x ∈ D , since x lies on no balls and D is the union of these balls (with no closure / interiors to force x to be in this set
Log in to reply
ok, i have to find a proof. Let C be the closed, compact square of side 1 , and B n be closed bounded balls of radius r n and center c n covering A = Int(C) , with intersection at most one point among two from them.
Take an open ball C n of radius r n + 2 1 0 5 0 0 0 0 0 1 and center c n and the perimeter of C covered with and open set E with a square ring shape with lenght 1 + 2 1 0 5 0 0 0 0 0 1 and width 2 1 0 5 0 0 0 0 0 1 . Since C is a compact set we can extract a finite covering from ( ∪ C n ) ∪ E , let's call ( ∪ n = 1 m C n ) ∪ E = F this finite covering, then ∪ n = 1 m C n can cover another compact square inside A ...
to be continued... ( In 3 days)
On the modified proof: The image of D under d ( x , − − ) is obviously a connected interval of the form ⟨ 0 , a ⟩ . If d ( x , y ) = 0 then x = y ∈ D so that x ∈ B n for some n , which you assumed was not the case. I see no reason why 0 itself should be a point of that interval.
[This is not a proper solution. It serves as a record for the discussions that we had when we weren't certain about the answer. We were offering various arguments in favor of "Yes". Similarly, in the other solution, you can see the various arguments in favor of "No".]
This discussion contains arguments why the answer should be Yes . Feel free to add your arguments or rebuttals in the comments, and I will summarize them.
-
If a point isn't yet covered, then it is a positive distance away from all the circles, and so we "should" be able to place a circle around the point.
However, this argument need not work if there are infinitely many circles, where the infimum of the distances from the circles is 0, and the circles "rotate" about the point. In particular, note that the naive argument of packing with maximal circles each time does not work. -
Erdös shows that we can pack the square with circles such that the limit of the leftover area is 0.
However, that doesn't mean that every single point is covered (since the measure of countably many points is 0). -
An analysis of a related problem is also given here .
-
Order all of the Q 2 points. We will create the circles in the following way:
Take the next point in the sequence. If it's already covered, do nothing. If it's not covered, since there are finitely many circles that are at a positive distance away, we can place a circle around this point. In the limit, the circles will cover every rational point.
Even though the covering is dense, it doesn't imply that every point is in the set (Do you see why?) Here's a counter example in 1-D, where we try to cover the segment [ 0 , 1 ] with closed line segments in a stupid way. Let i be an irrational number, and we use the sets [ i + 2 n 1 , i + 2 n − 1 1 ] , [ i − 2 n 1 , i − 2 n − 1 1 ] . Then, all the rational points are covered, but i will never be covered.
Moderator note:
We now know the answer is "No". Thanks for joining the conversation. Hope you gained from the experience.
Previous comment: We still do not know what the correct answer really is. Join in the discussion and help us figure this out.
Currently, I believe that the answer is no, and possibly that even an uncountable number of points cannot be covered.
Not quite the same. He's looking the at measure of the leftover area, and states that it goes to 0. However, this doesn't imply that the entire square is covered by (closed) discs.
For example (in the 1-D analogue), if we tried to cover the interval [ 0 , 1 ] with several closed intervals of the form [ 2 n + 1 1 , 2 n 1 ] , then even though the measure of the leftover length goes to 0, the point 0 is never covered by a closed interval. (This could make another interesting question. since we can modify this argument to leave out countably many points. )
To be fair, I do not know for certain what the answer is. After more thinking about it, I might be inclined to say that the answer is no. Note that we cannot cover the side of the square with discs (ignoring the corners), since that would require uncountably many discs, but we can only fit countably many discs in.
Log in to reply
Yes, I was wondering if his phrasing "almost all its area" was equivalent to "a covering", so I posted the link to get some feedback. I decided on the affirmative because we were having to cover "just" the interior, comparing it to an Apollonian Gasket where the set of interior points uncovered by a disc has measure 0 . However, I'm not comfortable enough with the fine details of measure theory to conclude definitively that this meant the square's interior was in fact fully covered. Perhaps an answer of "yes" or "no" depends on how one defines "cover".
Log in to reply
I assumed that we were supposed to say "yes" based on the convergence of the leftovers to zero (even though it arguably never gets there).
Log in to reply
@Steven Chase – The Yes/No answers are pretty evenly divided, and I'm also equally torn between the two.
I've set up the solution discussions to try and organize the arguments. Let's see how we can push this along.
That's one problem, what is a bona-fide "cover"? Is it something with an area of a limiting value of 1, or is it something that includes every single point inside the unit square? There can be an infinity of points "missed" by covering circles (disjoint discs) which areas total up to 1 as a limit value.
Log in to reply
@Michael Mendrin – Judging from point 5 in the outline of his proposed proof, Calvin would seem to be indicating that every single point must be covered, (which would appear to match this definition ). With Erdös' proof he was only concerned about the "exhaustion" of the area by disjoint discs, so we know that the answer for that type of cover is "yes", (which is why I chose that answer), but for the cover Calvin is talking about the answer is still up in the air, although his outline looks promising.
Log in to reply
@Brian Charlesworth – Okay, so, just to be clear, a full "cover" of the unit square includes every single point inside it, right? I think that should be noted in the problem definition. I was working on another "proof" of "exhaustion", but probably that's pointless (pun intended?) now.
Yes, that's what Calvin's "Issue 5" is about.
Log in to reply
@Michael Mendrin – Yes, I think that clarification should be added, as it would appear that at the very least you, Steven Chase and I all answered the question with a different definition in mind.
Log in to reply
@Brian Charlesworth – Alright. I've added "every single point" in. Is this much better?
Log in to reply
@Calvin Lin – Yes, that seems crystal clear now. :)
P.S.. Here is a discussion relevant to your proposed proof, although with the added restriction of requiring that all the circles have different radii. It also still doesn't address the critical "issue 5", but it does provide some good analysis and graphics.
Construct a covering of non-overlapping open discs, by centering disc U n on a rational point ( q 1 , q 2 ) not yet covered, and giving it a positive, transcendental radius (e.g. a π / b ) so that it does not overlap any other disc. Then the boundaries of these open discs are disjoint, so that the closures form a covering of closed discs. Also, by systematically working through the countably many rational points, we guarantee that each of them is covered. Since the countable points are dense, we will eventually (in the limit) cover the entire square.
Log in to reply
Because the rational points are a set of measure 0, and you are giving up control over the radius, I can cover the rational points by discs of total area < 1 (actually close to 0), which shows that this approach will not work.
Explicitly, take any ϵ > 0 (transcendental even), and cover the nth rational point by a disc of radius n ϵ . Then, the total area that is covered is ∑ n 2 π ϵ 2 = 6 π 3 ϵ 2 .
Playing devil's advocate, why must a non-rational point P be covered?
I believe the argument would go along the line of "Consider a sequence of rational points P i that converge to P . Each of these points is in a circle C i ". However, what we then need is that a circle contains infinitely many of these points P i . Otherwise, if each point P i is in a distinct circle C i , then I don't see an argument for which circle P would be in.
If you have a different argument to prove that P must be in a circle, please let me know.
Log in to reply
I agree that my approach does not work. Here is another consideration: shrink the square by removing a strip of width ϵ > 0 on all four sides. Then my covering of open sets would be an open covering of this shrunk square. Since the shrunk square is compact, this covering should have a finite sub-covering. But it is obvious that a covering with a finite number of discs leaves serious holes in the pattern!
Log in to reply
@Arjen Vreugdenhil – What you say is true. However, note that we're using closed discs instead of open discs.
I agree that if we used open discs, then we cannot cover all points. A direct argument would be that, no point on the boundary of an open disc could be covered by another non-overlapping open disc.
@Arjen Vreugdenhil – The comment was edited so this is no longer relevant. However, I'm leaving this up here as a further explanation for why a cover of a dense subset isn't sufficient.
I gave an explicit counter-example as to why you would not cover an area of 1.
An open cover of a dense set need not be the whole set. For example ( 0 , 1 ) is dense in [ 0 , 1 ] but the open cover is not the whole set.
What is true is that the closure of the dense set is the whole set. However, it is not sufficient that the union of (the closure of an open cover of the dense set) is the whole set. For example, take the space [ 0 , 1 ] , and a dense set is [ 0 , 1 ] − { 2 n 1 ). Then, an open cover of this dense set is ∪ ( 2 n + 1 1 , 2 n 1 , and the union of the closure is ∪ [ 2 n + 1 1 , 2 n 1 ] , which does not contain the point 0.
In terms of what I said earlier, if we take a sequence of points that converge to P = 0 , and consider the open sets in which they lie in, since there isn't an open set that covers infinitely many of these points, hence it doesn't necessarily follow that 0 is in the closure of a particular set. It is true that 0 is in the closure of the union, but it is not in the union of the closure (and these sets are not necessarily the same).
What is comes down to is this: even though a non-rational points P is surrounded by infinitely many rational points Q i at close distance, the radius of each of the circles I draw around Q i may be such that r i < P Q i , so that none of the circles actually contains P . How sad...
Log in to reply
That's a great way of putting it!
I must admit that this problem is tormenting me more than I initially expected it to.
I'm now almost fully convinced that the answer is no, but can't figure out a rigorous proof (in part due to the various conditions that I've thrown in to make the problem non-trivial).
Here's a possible way to prove it. There are some tedious details that I left out, and there might be technical/logical issues too.
- First, we draw in the unit circle, so each region is bounded on three sides by circles of integer curvature.
- Second, recall from descartes' circle theorem that if 3 circles are internally tangent to a circle, all of which have integer curvature, then the circle that is externally tangent to these 3 would have integer curvature.
- Third, we iteratively add circles that are internally tangent to three sides, which produces circles that are have integer curvature. Specifically, at step n , we only introduce circles that have curvature n .
- Fourth, show that "If we have circles with curvature a , b , c , and then we add the externally tangent circle of tangent d , then the regions that are not covered would be a perpendicular distance of at most f ( a , b , c ) from one of these 3 circles. It is clear that f ( a , b , c ) → 0 .
- Fifth, to show that a point P will eventually get covered, suppose P lies within the region of circles with curvature a , b , c . Let the distance of P from these circles be ϵ . Then, there exists a large enough N , such that if A , B , C < N , then f ( A , B , C ) < ϵ . Consider all of the circles of curvature up to N , then if P is not in any of these, then consider the region it is in. By selection of f ( A , B , C ) < ϵ , It is distance at least ϵ from the perimeters, hence will eventually be covered by the circle that we we place in this region.
Note: The condition of "integer curvature" isn't absolutely necessary, with the following fixes.
1. At step
n
, we could add in the finitely many circles that have curvature from
n
−
1
to
n
.
2. Show that if
a
,
b
,
c
,
are any real number less than
n
, then
f
(
a
,
b
,
c
)
>
ϵ
. Previously, when restricting to integers, this was a finite set, and so we know that a non-zero minimum exists.
Log in to reply
Unfortunately, (I believe that) this approach doesn't work. Here's the counter argument (and you should verify that the argument is correct)
The important properties that I will use are:
- These closed discs can only intersect at (at most) one point.
- The boundary of the inscribed circle can be split up amongst the non-filled regions.

Since each "triangle" region with an inscribed circle results in 4 "triangularish regions", we can simplify the argument where we simply use triangles. The state that we're in is similar to the Serpenski Triangle, where the white regions indicate discs we used, and the blue regions indicate the leftover area. (The blue regions do have a zero area/measure)
Now, given any triangle, we can index it by which iteration created it. In particular, at the nth iteration, we generate triangles of side legnth 2 n 1 . Given a triangle from the nth iteration, it is divided into 4 triangles in the (n+1)th iteration. We will label the center triangle 0, the top triangle 1, the bottom right triangle 2 and the bottom left triangle 3.
Given any triangle, we associate it to the finite sequence of triangles which tell us where it is located.
Given any point, we associate it to the (possibly infinite) sequence
t
1
t
2
t
3
,
…
in the following manner:
At the nth iteration, if it lies on triangle
i
, then
t
n
=
i
. For points on the perimeter, we can associate it with either triangle. This does implies that the sequence is not unique to the point. However, (it should be clear that) every sequence is associated to a unique point.
Note that once a point is in a triangle 0, we can ignore it and will no longer continue the sequence (also, a point in the interior of a triangle 0 will no longer be in any further triangles)
Note: For those who recognize the setup, the point t 1 t 2 t 3 … is the limit of the subsequence of triangles obtained by truncating the sequence.
Lemma: The point that is associated to the sequence t 1 t 2 t 3 , … can be defined in trillinear coordinates ( x , y , z ) in the following manner:
x = t i = 1 ∑ 2 i 1 , y = t i = 2 ∑ 2 i 1 , z = t i = 3 ∑ 2 i 1
This can be shown because if t i = 1 , then it means that we are in the top triangle, and hence we're 2 i 1 from the base.
Lemma:
Given any point and trilinear coordinates
(
x
,
y
,
z
)
, we will explain how to associate it to a sequnece.
At step
n
, if
x
≥
2
n
1
, then set
t
n
=
1
and replace
x
with
x
−
2
n
1
and go to step
n
+
1
.
Else if
y
≥
2
n
1
, then set
t
n
=
2
and replace
y
with
y
−
2
n
1
and go to step
n
+
1
.
Else if
z
≥
2
n
1
, then set
t
n
=
3
and replace
y
with
y
−
2
n
1
and go to step
n
+
1
.
Else set
t
n
=
0
and terminate the sequence.
Observation: You may have noticed that 2 3 3 3 3 3 3 … = 3 2 2 2 2 … . This is demonsrated in the above 2 facts, and this point is in fact the midpoint of the bottom base.
Lemma: The point 1 1 1 1 1 1 … corresponds to the top vertex of the triangle. This should be obvious, and follows from the trillinear coordinates since y = 0 , z = 0 .
Lemma: A point is on the bottom of the triangle if and only if it has a representation which consists only of 2's and 3's (and equivalently, all of its representations). Again, this follows from the trillinear coordinate since x = 0 .
Lemma: The representation satisfies t n = 1 for n > N if and only if lies on the bottom of of triangle t 1 t 2 … t N . This follows from the previous claim by restricting our attention to the triangle t 1 t 2 … t N .
Theorem:
Any point in which the number 1, 2, and 3 appear infinitely often and 0 never occurs, is not contained in the interior of a triangle 0, or on the perimeter of a triangle.
Proof:
If it was in the interior of a 0th triangle, then that index can only be 0. If it was on any perimeter, then the eventual sequence can contain at most 2 distinct digits. However, all 3 number occur infinitely.
Note: I believe that this argument can be extended to all scenarios where the circle that is added touches the perimeter, even if the regions have more than 3 sides. What we mostly require is that for each region t n , there is a subregion t m such that these 2 regions do not have a boundary/perimeter in common. This forces the limit point to not lie on any boundary.
Note: Having the circles touch at a point is crucial. I do not yet know how to extend this to the case where the circles do not touch.
Log in to reply
@Peter Byers This is the particular case, where the naive packing is "We draw in the unit circle, so each region is bounded on three sides by circles of integer curvature. Then, we iteratively add circles that are internally tangent to three sides". (The rooted comment offers my original train of thought, but I wasn't able to push through the argument properly, so I started trying to prove that it cannot be done.)
It turns out that in each region bounded by three sides, there is (at least) a point which cannot be covered by a disc. (Which unfortunately means that an uncountably infinite number of points are not covered.)
You might have to suspend belief that a disc can be interpreted as such a triangle (for ease of calculations, but it should be clear how the circle argument would work). The main property that I'm using is that any 2 of the "discs" intersect at only 1 point, and so the remaining regions will completely surround the disc added.
Log in to reply
@Calvin Lin – Thanks, I didn't see that post at first -- or saw it and took it to be a response to you by someone else.
That's very nice. I think it's also worth restating your conclusion as: for the given covering, there exists a sequence d j > 0 and a (fixed) point that is at least d j units away from shape j . (Note: For simplicity of notation, let's refer to the region outside the coverable region as "shape 0".) The question then can be stated as: is that true for any covering?
What's especially interesting about your argument is it not only shows that such a sequence exists for that particular covering, but it shows that d j can be defined as a fixed multiple of the size of shape j .
Log in to reply
@Peter Byers – Hi. I don't know a huge amount of rigorous pure mathematics, but could this problem be viewed as an inverse of attempting to square the circle? In that case, it is impossible to construct a sequence of circles (irrational) to equal a rational value.
My reason for the answer no is that the disc closest to a given corner has a positive radius (let's say R). So a point 0.2 R from the corner lies inside the square and outside any disc. Am I missing something?
Log in to reply
It is not necessary that there is such a disc.
For example, there are an infinite number of real numbers near 1, but there is no nearest real number.
Because we can use infinitely many discs, we cannot necessarily refer to the unique disc that is closest to a given point. Agnishom's example of the real numbers gives an illustration of this.
In particular, note that the naive argument of packing with maximal circles each time does not work.
Has that been proven?
As one works through the problem, there are several main themes/ideas that crop up. We list them here for reference. See if you caught these points, as they will be crucial in the proof / understanding this problem better.
Prove by contradiction. Tl; dr: We will count the number of points in which a pair of circles are tangential. Using one approach, we will show that the number is countable. Using another approach, we will show that the number is uncountable.
Suppose that such a cover exists.
Showing that number of tangency points is countable
Lemma: There are at most countably many discs in the cover.
Proof: Every disc (of positive radius) must contain a point whose coordinates are both rational. (Explicit construction: there is a rational q such that the intersection of x = q and this disc is a closed interval of non-zero length. In this interval, pick a rational number r . Then ( q , r ) is in this disc).
This creates an injection from the discs to Q × Q , hence there are at most countably many discs. □ .
Note: It should be obvious that finitely many discs would not cover the square. Hence, if a cover exists, there has to be countably infinitely many discs.
Since every 2 discs intersect at at most 1 tangency point, and we have countably many pairs of discs, thus there are at most countably many tangency points.
Showing that number of tangency points is uncountable
Theorem: The interval ( 0 , 1 ) cannot be expressed as the disjoint union of countably many closed intervals (possibly of 0 length).
We will use this theorem without proof as it requires advanced material. It can be proven topologically using a cantor set -esque counting argument, or analytically with Baire Category theorem.
Corollary of theorem: Consider ( 0 , 1 ) , inheriting the topology on the real line. If ( 0 , 1 ) is expressed as the union of countably many closed intervals, then either it is a single interval ( 0 , 1 ) (which is closed in ( 0 , 1 ) ), or there are 2 intervals that are not disjoint (meaning that they intersect).
Lemma: Any line through the square that is not x = 2 1 or y = 2 1 , has to pass through a tangency point of 2 discs.
Proof: Take any line and consider its intersection with each of the discs, which gives us closed intervals whose union is ( 0 , 1 ) . By the corollary,
Now, consider the lines of the form x = r , for some real number 0 < r < 1 , r = 2 1 . Each line will yield us (at least) a tangency point of 2 discs. Hence, we have uncountably many such tangency points.
Thus we have a contradiction, so no such cover is possible. □
Corollary: In any closed disc cover, there are uncountably many points that are uncovered!
Hint to corollary: Consider what happens when we allow for countably many discs of zero radius.
Generalization: Do you see how this proof can be generalized?
In particular, we cannot cover the open unit circle with smaller (closed) squares if the squares are only allowed to pairwise intersect at one point (instead of on an entire side).
Previous notes:
This is not a proper solution, just a basis for discussion. We do not know if the answer is indeed Yes or No.
This discussion contains arguments why the answer should be No . Feel free to add your arguments or rebuttals in the comments, and I will summarize them.