Almost completely empty
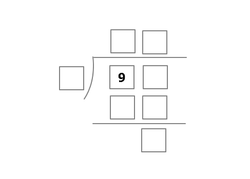The above shows a condensed form of long division between 2 integers, with the last box at the bottom representing the remainder of the quotient. Each box represents a
distinct
single digit non-negative integer.
What are the two integers that are not used?
Submit your answer as the product of these two integers.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Since all digits are distinct, the box below 9 must be equal to 8.
Now, we note that the reminder cant be equal to 0, this is because there would be same number below the nine. we eliminate 1. if it is two, it can not be <90. so eliminated.
If it is 3 the result is 3 0 something so eliminated.
If it is four, the below would be 8 8 , hence eliminated.
If it is five, it cant be less than 90 ,hence eliminated.
At 6 it cant be<90 hence eliminated.
At 8 the below will be 8 8 .
At 9 it can't be less than 90. we check 7 as it is the only one alive.
Yes! it works. we see the required numbers are 3 and 5. the product is 1 5 .