Variable resistor in circuit
A circuit is set up as shown. If the variable resistor's resistance begins at 2 Ω and increases at a rate of 1 Ω per second, what is the power generated by one bulb after 10 seconds? If this power can be expressed as P = b 2 a 2 W , where a and b are positive coprime integers, find a + b .
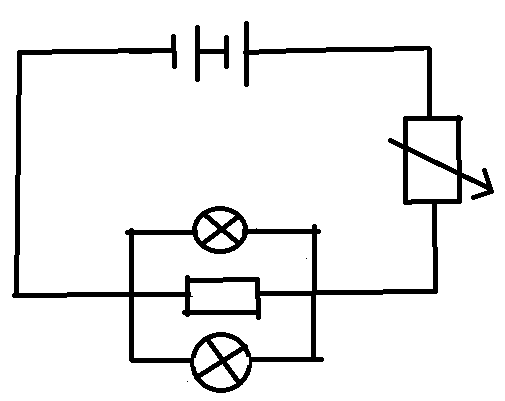
Details:
- The voltage of the battery is 2 4 V .
- The resistance of the resistor is 6 Ω .
- The bulbs are identical and each have a resistance of 4 Ω .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Charley Feng , you have to mention that a and b are positive coprime integers, because other then 3 4 is a solution, 6 8 , 9 1 2 , 1 2 1 6 , ⋯ are also solutions. There are infinitely many solutions.
A good follow-up would be to ask for the total energy dissipated in one bulb from t = 0 to t = 1 0
do you mean in a separate problem?
Log in to reply
Yeah, a "Part 2" problem
Log in to reply
yea just do it because I don't really know how to do it yet
Mind if I post it, or do you want to?
I solved this problem as you mentioned
P ( t ) P ( 1 0 ) = R 4 ( V b ( t ) ) 2 = 4 ( 7 + 2 t ) 2 7 2 2 = 4 ( 2 7 2 ) 7 2 2 = 3 2 4 2 W where R b is the resistance of a bulb.
Therefore, a + b = 4 + 3 = 7 .