Complex Flux

A hollow sphere of radius $R$ of uniform surface charge density $\sigma$ , its center is placed at origin $A$ .

A hollow hemispherical surface of $R$ is at centre $B$ $(x-2) ^{2}+y^{2}+z^{2}=1,x≥2$

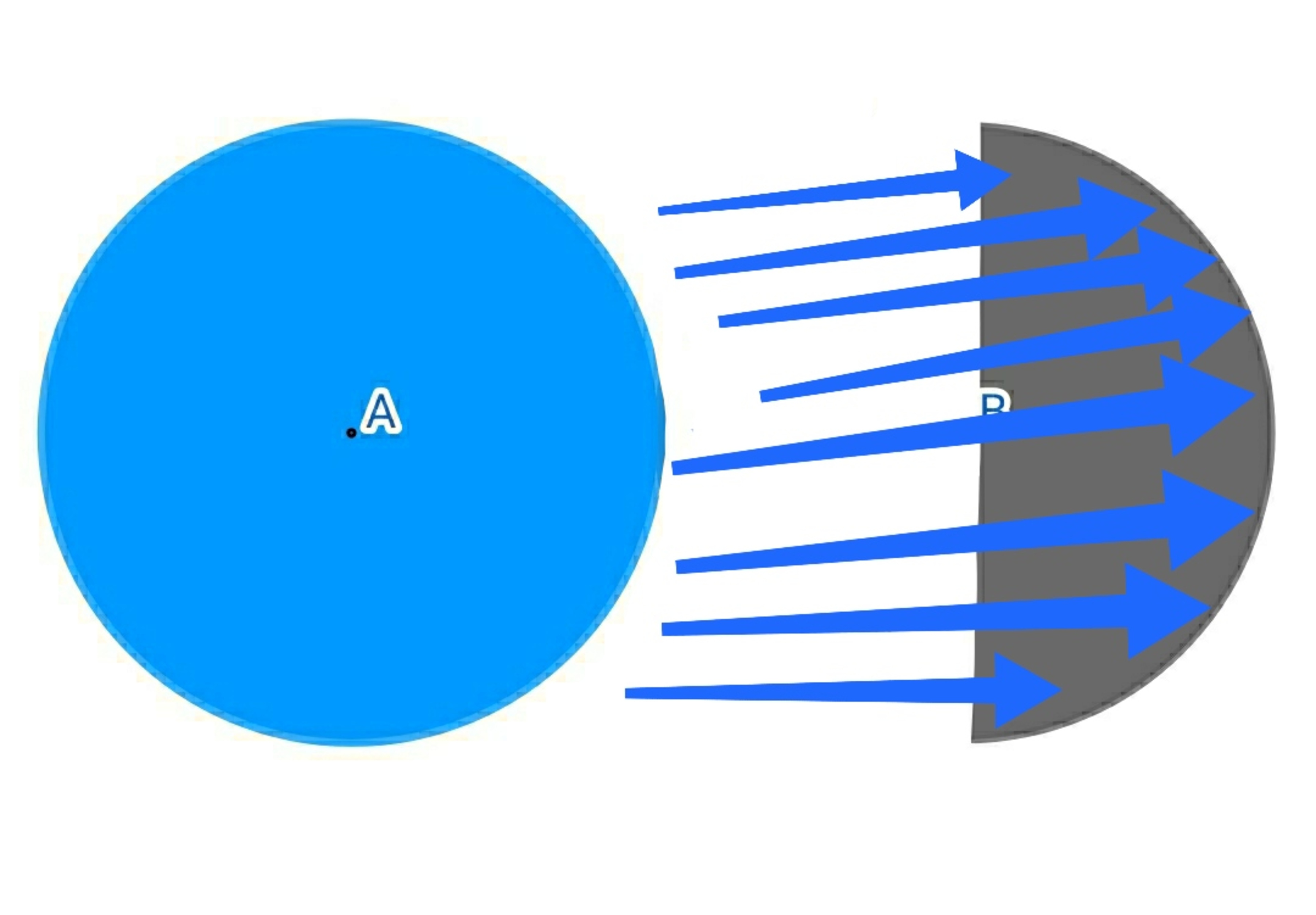
Find the electric flux through the curved surface of that hemisphere due to that hollow uniformly charged sphere.

Details and Assumptions
1) $R=1$
2) Coordinates of $A$ and $B$ are $(0,0,0$ and $(2,0,0)$ respectively.
3) $\sigma=1$
4) Electric permittivity $\epsilon_{0}=1$
5) I have provided a two dimensional figure. But this system is in three dimensions. I have provided the view of figure from $-Y$ axis.
6) The answer is positive.

This problem is original.

This problem is dedicated to my respected teacher Steven Chase