C \mathbb{C} omplex-icated Cauchy Contour Crescent Curve

Calculus Level 5

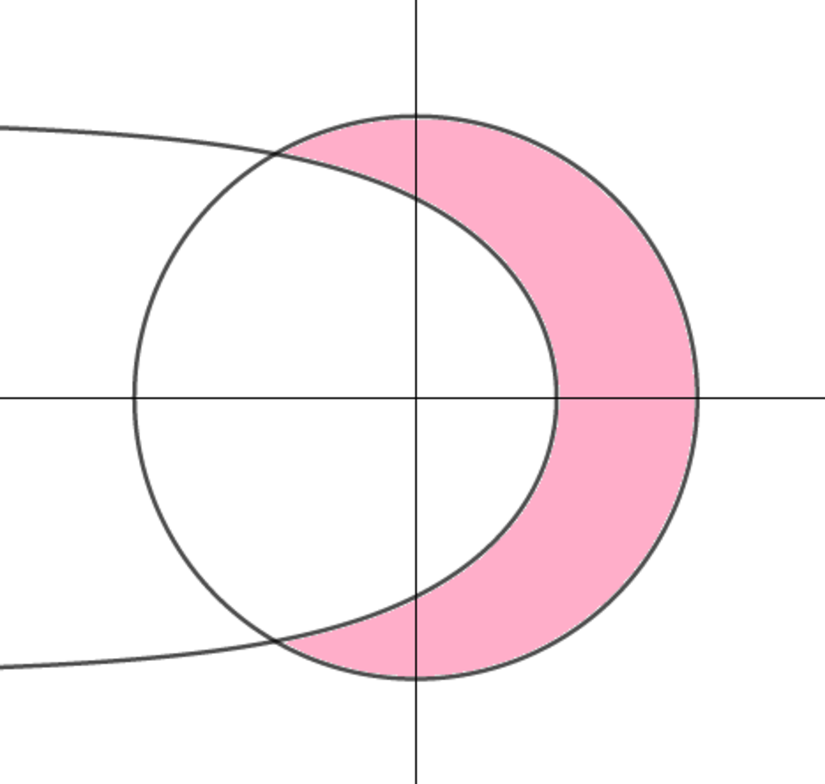
Let z z denote a complex number. Two sets of complex numbers -- one satisfying ∣ z ∣ = 1 |z| = 1 and another ∣ z + ∣ z ∣ ∣ = 1 |z + |z|| = 1 -- are illustrated in the Argand plane as shown on the right. If the area of the pink region can be expressed as

A B π − C D E \dfrac{A}{B}\pi - \dfrac{C}{D}\sqrt{E}

where A A , B B , C C , D D , and E E are positive integers, gcd ⁡ ( A , B ) = gcd ⁡ ( C , D ) = 1 \gcd(A,B) = \gcd(C,D) = 1 , and E E is square-free, input A + B + C + D + E A + B + C + D + E as your answer.

Bonus. For fun, try finding different ways of solving the problem.


The answer is 11.

Michael Huang by Michael Huang , 29, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Mark Hennings
Feb 5, 2021

Using polar coordinates, the noncircular curve is defined by 1 = ∣ r ( cos ⁡ θ + 1 ) + i r sin ⁡ θ ∣ = ∣ 2 r cos ⁡ 1 2 θ ( cos ⁡ 1 2 θ + i sin ⁡ 1 2 θ ) ∣ = 2 r cos ⁡ 1 2 θ 1=\big|r(\cos\theta+1)+i r\sin\theta\big| = \big|2r\cos\tfrac12\theta(\cos\tfrac12\theta+i\sin\tfrac12\theta)\big| \; = \; 2r\cos\tfrac12\theta so the curve is r = 1 2 sec ⁡ 1 2 θ ∣ θ ∣ < π r \; = \; \tfrac12\sec\tfrac12\theta \hspace{2cm} |\theta| < \pi Thus we want 1 2 ∫ − 2 3 π 2 3 π ( 1 − 1 4 sec ⁡ 2 1 2 θ ) d θ = 1 2 [ θ − 1 2 tan ⁡ 1 2 θ ] − 2 3 π 2 3 π = 2 3 π − 1 2 3 \tfrac12\int_{-\frac23\pi}^{\frac23\pi}\big(1 - \tfrac14\sec^2\tfrac12\theta\big)\,d\theta \; = \; \tfrac12\Big[ \theta - \tfrac12\tan\tfrac12\theta\Big]_{-\frac23\pi}^{\frac23\pi} \; = \; \tfrac23\pi - \tfrac12\sqrt{3} making the answer 2 + 3 + 1 + 2 + 3 = 11 2+3+1+2+3 = \boxed{11} .

3 Helpful 2 Interesting 4 Brilliant 0 Confused

If possible could you give me a little more detail on the integration part please, as I am not at all familiar with polar coordinate integration ( more on how you got the integral, as I understand how the integration was done )

Jason Gomez - 4 months, 1 week ago

Log in to reply

If we have a curve defined in polar coordiantes by the equation r = f ( θ ) r = f(\theta) , the area swept out between angles α \alpha and β \beta is 1 2 ∫ α β f ( θ ) 2 d θ \tfrac12\int_\alpha^\beta f(\theta)^2\,d\theta Check out this Wiki .

In this question, I want the area between the curves r = 1 r = 1 and r = 1 2 sec ⁡ 1 2 θ r = \tfrac12\sec\tfrac12\theta in the range − 2 3 π < θ < 2 3 π -\tfrac23\pi < \theta < \tfrac23\pi (the two curves intersect when θ = ± 2 3 π \theta = \pm\tfrac23\pi ). The rest is standard integration.

Mark Hennings - 4 months, 1 week ago

Log in to reply

Thanks a lot, just checking, this is like doing Riemann sums on sectors of a circle right, looks quite powerful

Jason Gomez - 4 months, 1 week ago

Log in to reply

@Jason Gomez – Yes, it can be thought of that way, where each δ θ \delta\theta element is approximated as a triangle.

Mark Hennings - 4 months, 1 week ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...