Complex solutions
x , y and z are complex numbers such that
{ x + y + z ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 = 2 0 = x y z .
What is the value of x y z x 3 + y 3 + z 3 ?
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
37 solutions
Moderator note:
Nicely done!
Same method applied.
I did the same ...
Same method using the identities
In problems like this, I find it convenient to express everything using the possible symmetric polynoms of three variables, up to the appropriate degree. I have never seen the relations between them tabulated anywhere, but you can produce them whenever they are needed. We have ( x + y + z ) 2 = x 2 + y 2 + z 2 + 2 ( x y + y z + z x ) . ( x + y + z ) 3 = x 3 + y 3 + z 3 + 3 ( x y 2 + y x 2 + x z 2 + z x 2 + y z 2 + z y 2 ) + 3 x y z . So far, we can call x + y + z = A , x 2 + y 2 + z 2 = B , x y + y z + z y = C , x 3 + y 3 + z 3 = D , x y 2 + y x 2 + x z 2 + z x 2 + y z 2 + z y 2 = E , x y z = F . So we have A 2 = B + 2 C , A 3 = D + 3 E + 3 F . Two more relations of order 3 or less turn out to be A B = D + E and A C = E + 3 F . With A = 2 0 and what comes from expanding the second equation in the problem, substituting E, we get four linear equations for B,C,D and E, and so can find all values. Actually, we can use just two of the equations to get D = 1 3 F , which is what the other solvers here have done by various ingenious inspection.
Log in to reply
Symetric polynomials were (unhappily) not needed here. Shorter proofs provided above.
Log in to reply
It's something to try while you're working on the solution though. I'm sure the short proofs weren't the first thing the posters tried.
Did exactly in the same way......................
Did the same way ..
I did the process in my mind!
let's assume x=0,and we can get y+z=20,yz=400/3,has solution 10+10i/sqrt(3) and 10-10i/sqrt(3) fit for both condition.so at this situation the answer is NO
We know that x 3 + y 3 + z 3 − 3 x y z = 2 1 ( x + y + z ) ( ( x − y ) 2 + ( x − z ) 2 + ( y − z ) 2 ) = 1 0 x y z . Dividing both sides by x y z and adding 3 to both sides gives x y z x 3 + y 3 + z 3 = 1 3 .
If you didn't know the first fact, I recommend Titu Andreescu's "Mathematical Olympiad Treasures" to you. Great read.
Moderator note:
Nicely done!
did the same thing !!
x y z x 3 + y 3 + z 3 = x y z ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x ) + 3 x y z = x y z ( 2 0 ) ( 2 x y z ) + 3 x y z = 1 0 + 3 = 1 3
Moderator note:
Nicely done!
So many correct and nice solutions, that it is impossible to choose the best.
I did this the exact same way
Did the same mentally
Did the same.
We use the identity, x 3 + y 3 + z 3 − 3 x y z = 2 1 ( x + y + z ) ( ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 ) .Then x y z x 3 + y 3 + z 3 = 2 1 ( x + y + z ) + 3 = 1 0 + 3 = 1 3 .
x y z x 3 + y 3 + z 3 = 2 ∗ ( x y z ) ( x + y + z ) { ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 } + 3 Putting the appropriate values as given in the problem, we get, x y z x 3 + y 3 + z 3 = 1 3
that is exactly wat I did!! cool
First note that : ( x + y + z ) [ ( x − y ) 2 + ( x − z ) 2 + ( y − z ) 2 ] = x 3 + y 3 + z 3 − 3 x y z .
Multiply the second equation with x + y + z , to get : 2 ( x 3 + y 3 + z 3 − 3 x y z ) = 2 0 x y z ⟹ 2 ( x 3 + y 3 + z 3 ) = 2 6 x y z . From here we see that : x y z x 3 + y 3 + z 3 = 2 2 6 = 1 3 .
My solution using polynomials: Let x + y + z = p , x y + z x + y z = q , x y z = r Equation 1 gives that p = 2 0 Equation 2 gives on expansion: 2 ( x 2 + y 2 + z 2 ) − 2 ( x y + y z + z x ) = x y z ⇒ x 2 + y 2 + z 2 = 2 r + 2 q
Let P ( m ) be a polynomial such that P ( m ) = ( m − x ) ( m − y ) ( m − z ) = m 3 − p m 2 + q m − r so P ( x ) = P ( y ) = P ( z ) = 0 .
P ( x ) = 0 ⇒ x 3 − p x 2 + q x − r = 0 ⇒ x 3 = p x 2 − q x + r and similarly for y , z
Adding the three equations together gives: x 3 + y 3 + z 3 = p ( x 2 + y 2 + z 2 ) − ( x + y + z ) + 3 r = p ( 2 r + 2 q ) − p q + 3 r = 2 p r + 6 r by the earlier equation.
Hence we have: x y z x 3 + y 3 + z 3 = r ( 2 p r + 6 r ) = 2 p + 6 = 2 2 0 + 6 = 1 3
Your solution is really practical and inspiring. Not Until I looked at your solution did I realize that I had used such method before. I should have If I had noted that x+y+z xy+xz+yz xyz all make up this problem. Really nice :)
Observe that ( x + y + z ) 3 = ∑ ( x 3 ) + 3 ∑ ( x 2 ( y + z ) ) + 6 x y z = − 2 ∑ ( x 3 ) + 3 ∑ ( x 2 ( x + y + z ) ) + 6 x y z ; Add and subtract 3 ∑ ( x 3 ) = − 2 ∑ ( x 3 ) + 3 ( x + y + z ) ∑ ( x 2 ) + 6 x y z
Now, squaring the first equation and adding it to the second equation (given ones) gives us: 3 ∑ ( x 2 ) = 2 0 2 + x y z
Plugging this in the result we obtained gives: ( x + y + z ) 3 = − 2 ∑ ( x 3 ) + ( x + y + z ) ( 2 0 2 + x y z ) + 6 x y z
Simplifying and plugging the value of x + y + z = 2 0 gives the answer as 1 3 .
Man! I had to think a heck lot for this :D
Label the two given equations ( 1 ) and ( 2 ) . Expanding ( 2 ) gives 2 ( x 2 + y 2 + z 2 ) − 2 ( x y + x z + y z ) = x y z . ( 3 ) Now we square both sides of ( 1 ) to get x 2 + y 2 + z 2 + 2 ( x y + x z + y z ) = 4 0 0 . We multiply this equation by 2 and subtract equation ( 3 ) : 6 ( x y + x z + y z ) = 8 0 0 − x y z . ( 4 )
At this point we return to equation ( 1 ) , which we cube both sides of and factor: x 3 + y 3 + z 3 + 3 [ x y ( x + y ) + x z ( x + z ) + y z ( y + z ) ] + 6 x y z = 8 0 0 0 . Using equation ( 1 ) , we can replace each of the sums x + y , x + z , y + z with 2 0 − z , 2 0 − y , 2 0 − x . Therefore, we have x 3 + y 3 + z 3 + 3 [ x y ( 2 0 − z ) + x z ( 2 0 − y ) + y z ( 2 0 − x ) ] + 6 x y z = 8 0 0 0 x 3 + y 3 + z 3 + 6 0 ( x y + x z + y z ) − 3 x y z = 8 0 0 0
We multiply equation ( 4 ) by 1 0 to get 6 0 ( x y + x z + y z ) = 8 0 0 0 − 1 0 x y z . Now we substitute into the previous equation: x 3 + y 3 + z 3 + 8 0 0 0 − 1 0 x y z − 3 x y z = 8 0 0 0 , or x 3 + y 3 + z 3 = 1 3 x y z . Thus, x y z x 3 + y 3 + z 3 = 1 3 .
That's a lot of work. You should have used this identity instead: x 3 + y 3 + z 3 − 3 x y z = ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x ) , that would have made the solution to this problem really really short.
Log in to reply
Yeah, I should have, but I didn't know that equation exactly.
we know that
x 3 + y 3 + z 3 = ( x + y + z ) 3 − 6 x y z − 3 x y z ( x + y + z ) ( x 1 + y 1 + z 1 ) + 9 x y z
From two given equation we have
3 x y z ( x + y + z ) 3 − 6 1 = x 1 + y 1 + z 1
hence
x y z x 3 + y 3 + z 3 = x y z 2 0 3 − 6 − ( x y z 2 0 3 − 1 0 ) + 9
x y z x 3 + y 3 + z 3 = 1 3
We know that x^3+y^3+z^3-3xyz=(0.5)(x+y+z){(x−y)^2+(y−z)^2+(z−x)^2}
=>x^3+y^3+z^3-3xyz=10xyz(putting the values)
=>x^3+y^3+z^3=13xyz
=>(x^3+y^3+z^3)/xyz=13 . (sorry , i don't know how to use latex )
We have x 3 + y 3 + z 3 − 3 x y z = 2 1 ( x + y + z ) [ ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 ] . Thus, x 3 + y 3 + z 3 = 1 3 x y z
sin a + sin b = 2 sin ( 2 a + b ) cos ( 2 a − b )
Similarly for c and d . Adding both gives:
0 = sin a + sin b + sin c + sin d =
(using c + d = − ( a + b ) )
= 2 sin ( 2 a + b ) ( cos ( 2 a − b ) − cos ( 2 c − d ) ) =
(using c − d = ( a + c ) + ( b + c ) and a − b = ( a + c ) − ( b + c ) )
= 4 sin ( 2 a + b ) sin ( 2 a + c ) sin ( 2 b + c )
which leads to: a = − b or a = − c or b = − c .
Now use the counting already explained by Thomas B.
Let a cubic equation of the form n 3 + a n 2 + b n + c = 0 have roots equivalent to x, y, and z.
By Vieta's theorem, the root-coefficient relationships are written as follows: x+y+z = -a, xy + yz + xz = b, xyz = -c.
The first equation in the problem can be combined with the first root-coefficient relationship to yield a = -20. The second equation in the problem can be expanded and simplified as follows: 2 ( x 2 + y 2 + z 2 ) − 2 ( x y + y z + x z ) = x y z 2 ( ( x + y + z ) 2 − 2 ( x y + y z + x z ) ) − 2 ( x y + y z + x z ) = x y z 2 ( x + y + z ) 2 − 6 ( x y + y z + x z ) = x y z
The root-coefficient relationships then allow this to be rewritten as: 2 a 2 − 6 b = − c , or c = − 2 ( a 2 − 3 b )
The final expression, x y z x 3 + y 3 + z 3 , is simplified in this manner: = x y z x 3 + y 3 + z 3 − 3 x y z + 3 x y z = x y z ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − x z ) + 3 x y z = x y z ( x + y + z ) ( ( x + y + z ) 2 − 3 ( x y − y z − x z ) ) + 3 x y z Writing in terms of a, b, and c: = − c ( − a ) ( a 2 − 3 b ) − 3 c = 3 + c ( a ) ( a 2 − 3 b )
From the earlier calculations: c = − 2 ( a 2 − 3 b ) , a = -20: = 3 + − 2 ( a 2 − 3 b ( a ) ( a 2 − 3 b ) = 3 + − 2 a = 3 + − 2 − 2 0
=13
We have x 3 + y 3 + z 3 − 3 x y z = ( x + y ) 3 − 3 x y ( x + y ) + z 3 − 3 x y z
= ( x + y + z ) ( ( x + y ) 2 − ( x + y ) z + z 2 ) − 3 x y ( x + y + z ) = ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x ) = ( x + y + z ) ( 2 1 ( ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 ) )
Now, by substituting the values given, we have: x 3 + y 3 + z 3 − 3 x y z = 2 0 2 1 ( x y z ) or x 3 + y 3 + z 3 = 1 3 x y z
Hence, 13 is the answer we desired.
Note that ( x + y + z ) [ ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 ] = 2 ( x 3 + y 3 + z 3 − 3 x y z ) . So,
2 6 x y z = 2 ( x 3 + y 3 + z 3 ) and thus x y z x 3 + y 3 + z 3 = 1 3 .
We will need 3 equations to solve for the values of all three numbers, since we were given only 2 we need to express the desired expression in terms of the variables above.
Expanding the LHS of the second equation will yield,
2 ( x 2 + y 2 + z 2 − x y − y z − x z ) = x y z
Multiplying the LHS of the first equation to both sides of the second equation will yield:
2 x 3 + 2 y 3 + 2 z 3 − 6 x y z = x y z ( x + y + z )
Now if we solve for x 3 + y 3 + z 3 in the new equation, we shall have the numerator of the algebraic expression we are asked to find. So,
x 3 + y 3 + z 3 = ( 1 / 2 ) ( x y z ( x + y + z ) + 6 x y z )
With then if we divide it by x y z we'll arrive at the desired answer. Thus,
x y z x 3 + y 3 + z 3 = ( 1 / 2 ) ( x + y + z + 6 )
And substituting 2 0 to x + y + z we will get the answer:
x y z x 3 + y 3 + z 3 = ( 1 / 2 ) ( 2 0 + 6 )
x y z x 3 + y 3 + z 3 = ( 1 / 2 ) ( 2 6 )
x y z x 3 + y 3 + z 3 = 1 3
Given : ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 = x y z
On multiplying by two on both sides, we get - 2 1 ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 = 2 1 x y z ⇒ x 2 + y 2 + z 2 − x y − y z − z x = 2 1 x y z
Now we multiply by x + y + z on both sides, we get - ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x ) = 2 1 ( x y z ) ( x + y + z ) ⇒ x 3 + y 3 + z 3 − 3 x y z = 2 1 ( x y z ) ( x + y + z )
But x + y + z = 2 0 , so ⇒ x 3 + y 3 + z 3 − 3 x y z = 2 1 ( x y z ) . 2 0 = 1 0 x y z ⇒ x 3 + y 3 + z 3 = 1 3 x y z x y z x 3 + y 3 + z 3 = 1 3
( x + y + z ) 2 = 4 0 0
x 2 + y 2 + z 2 = 4 0 0 − ( 2 x y + 2 x z + 2 y z ) .....(1)
( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 = x y z
2 x 2 + 2 y 2 + 2 z 2 − 2 x y − 2 x z − 2 y z = x y z .....(2)
substitute (1) to (2)
8 0 0 − 6 ( x y + x z + y z ) = x y z
x y + x z + y z = 6 8 0 0 − x y z
x 3 + y 3 + z 3 = ( x + y + z ) 3 − 3 ( x + y + z ) ( x y + x z + y z ) + 3 x y z
x 3 + y 3 + z 3 = 8 0 0 0 − 6 0 ( 6 8 0 0 − x y z ) + 3 x y z
x 3 + y 3 + z 3 = 1 3 x y z
so the answer is 1 3 .
multiply both equations
(x+y+z)[(x−y)^2+(y−z)^2+(z−x)^2]=20xyz.
=>(x+y+z)(x2+y2+z2−xy−yz−zx)=10xyz.
x^3+y^3+z^3−3xyz=10xyz
x^3+y^3+z^3=13xyz
(x^3+y^3+z^3)/xyz=13
From ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 = x y z , we have 2 ( x 2 + y 2 + z 2 − x y − y z − z x ) = x y z
We have: x y z x 3 + y 3 + z 3 − 3 = x y z x 3 + y 3 + z 3 − 3 x y z
= x y z ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x ) = 2 0 . 2 1 = 1 0
Therefore, x y z x 3 + y 3 + z 3 = 1 3
Expand the second equation you will get x 2 + y 2 + z 2 − x y − y z − x z = x y z / 2
Then multiplies both sides by 20, you will get ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − x z ) = 1 0 x y z
By solving this equation, you will get x 3 + y 3 + z 3 − 3 x y z = 1 0 x y z
Therefore, ( x 3 + y 3 + z 3 ) / x y z = 1 3
Note: The reason for stating that they are complex numbers, is to ensure that the system of equations has a solution. Otherwise, we cannot conclude what the non-existant value is.
IE If you are told " x is a real number such that x 2 = − 1 , find x 4 ", then the answer isn't x 4 = ( x 2 ) 2 = 1 , but instead it should be "no solution".
By using the second given condition We get x^2 + y^2 + z^2 - xy - yz -xz = xyz/2 Now using identity x^3 + y^3 + z^3 - 3xyz = (x+y+z)(x^2 + y^2 + z^2 - xy - yz -xz) We get x^3 + y^3 + z^3 = 13xyz Hence answer is 13.
we know that x^3 + y^3 + z^3 = ( x^2 + y^2 + z^2 - xy - yz - zx ) * ( x+y+z) ...... (1) (x-y)^2 + (y-z)^2 + (z-x)^2 = 2 ( x^2 + y^2 + z^2 - xy - yz - zx ) = xyz ..........(2) PUT x+y+z=20 in eqn (1) ........... x^3 + y^3 + z^3 = 20 * ( xyz / 2 )
Use => a^3 + b^3 + c^3 - 3abc = (a + b + c)(a^2 + b^2 + c^2 - ab - ac - bc). and replace ∑(x-y)^2 with => 2(x^2+y^2+z^2 - xy-yz-zx) .. :) Found it easier than usual level 4 questions..
Moderator note:
How are you applying the first line of your solutions with the second line of your solution?
Unfortunately, not all of us are mind readers, and can only deduce from what you have written down.
Multiply both equations together: (x+y+z) [x^2 - 2xy + y^2 + y^2 - 2zy + z^2 + z^2 - 2xz + x^2] = 20xyz (x+y+z)(x^2+y^2+z^2 - xy - yz - xz) = 10xyz x^3 + y^3 + z^3 − 3xyz = 10xyz x^3 + y^3 + z^3 = 13xyz (x^3 + y^3 + z^3) / xyz = 13
Very easy problem for 180 points...
First, let's show some identities...
2 1 ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 = x 2 + y 2 + z 2 − x y − y z − z x
⟹ ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 = 2 ( x 2 + y 2 + z 2 − x y − y z − z x )
And, ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x ) = x 3 + y 3 + z 3 − 3 x y z
Now, let's multiply the two equations in the question...
( x + y + z ) ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 = 2 0 x y z
⟹ ( x + y + z ) × 2 ( x 2 + y 2 + z 2 − x y − y z − z x ) = 2 0 x y z
⟹ ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x ) = 1 0 x y z
⟹ x 3 + y 3 + z 3 − 3 x y z = 1 0 x y z
⟹ x 3 + y 3 + z 3 = 1 3 x y z
⟹ x y z x 3 + y 3 + z 3 = 1 3
Hence, the required answer is 1 3
"very easy" depends on what identities you had memorized I guess; I didn't know the (x+y+z) (xx+yy+zz-xy-yz-zx) one , so it took a lot of things tried before I foind a line of enquiry that worked.
Log in to reply
These identities are very well-known... That's why I didn't find it important to prove these... Anyway, accidentally if someone didn't face them, I'm illustrating the identities for them in comment! :)
1st one:
( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2
= ( x 2 − 2 x y + y 2 ) + ( y 2 − 2 y z + z 2 ) + ( z 2 − 2 z x + x 2 )
= 2 x 2 + 2 y 2 + 2 z 2 − 2 x y − 2 y z − 2 z x
= 2 ( x 2 + y 2 + z 2 − x y − y z − z x )
2nd one:
x 3 + y 3 + z 3 − 3 x y z
= ( x + y ) 3 − 3 x y ( x + y ) + z 3 − 3 x y z
= ( x + y ) 3 + z 3 − 3 x y ( x + y + z )
= ( x + y + z ) ( ( x + y ) 2 − ( x + y ) z + z 2 ) − 3 x y ( x + y + z )
= ( x + y + z ) ( x 2 + 2 x y + y 2 − y z − z x + z 2 ) − 3 x y ( x + y + z )
= ( x + y + z ) ( x 2 + y 2 + z 2 + 2 x y − y z − z x − 3 x y )
= ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x )
You missed a bracket in the first identity. It should be like this:
2 1 ( ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 ) = x 2 + y 2 + z 2 − x y − y z − z x
Log in to reply
Noooooooo, not again!!! :-( I missed bracket in two places!!! Second one where I multiplied two equations!!! >:o That should look like this...
( x + y + z ) ( ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 ) = 2 0 x y z
Log in to reply
Don't worry! Most people don't care about silly typos like these. But it could be confusing for people who don't know how to solve the problem and are trying learn from your solution. That's why I pointed it out.
It is always good to read your whole solution before posting it as it avoids typos like these.
Since x^3+y^3+z^3 - 3xyz = (x+y+z)1/2( (x-y)^2 + (y-z)^2 + (z-x)^2 ) = 20/2 (xyz)= 10xyz so x^3+y^3+z^3 = 13xyz and finally x^3+y^3+z^3/xyz = 13
1/2{(x−y)^2+(y−z)^2+(z−x)^2}=1/2xyz. (x^3+y^3+z^3)/xyz = [1/2xyz(x+y+z)+3xyz]/xyz =13
Note that x 3 + y 3 + z 3 − 3 x y z = ( x + y + z ) ( x 2 + y 2 + z 2 − x y − z y − z x )
From equation ( 2 ), we have that x y z = 2 ( x 2 + y 2 + z 2 − x y − z y − z x )
So x 3 + y 3 + z 3 = 2 x y z ( x + y + z ) − 3 x y z
From equation ( 1 ) we have that x + y + z = 2 0
So x 3 + y 3 + z 3 = 1 0 x y z + 3 x y z
Therefore x y z x 3 + y 3 + z 3 = x y z 1 3 x y z = 1 3
Thus the required answer is 1 3
Multiply both equations to get: ( x + y + z ) ∗ ( ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 ) = 2 0 x y z ( x + y + z ) ∗ ( x 2 + y 2 + z 2 − x y − y z − z x ) = 1 0 x y z x 3 + y 3 + z 3 − 3 x y z = 1 0 x y z x 3 + y 3 + z 3 = 1 3 x y z ( x 3 + y 3 + z 3 ) : ( x y z ) = 1 3
Expanding: 2 x 2 + 2 y 2 + 2 z 2 − 2 x y − 2 x z − 2 y z = x y z Recall the useful identity: x 3 + y 3 + z 3 − 3 x y z = ( x + y + z ) ( x 2 + y 2 + z 2 − − x y − x z − y z ) Now, we can find x 3 + y 3 + z 3 : x 3 + y 3 + z 3 = 2 0 ( 2 x y z ) + 3 x y z = 1 0 x y z + 3 x y z = 1 3 x y z The answer is 1 3 .
First, note that x 3 + y 3 + z 3 − 3 x y z = ( x + y + z ) ( x 2 + y 2 + z 2 − x y − x z − y z ) and that ( x − y ) 2 + ( x − z ) 2 + ( y − z ) 2 = 2 ( x 2 + y 2 + z 2 − x y − x z − y z ) .
Then it follows that
x y z x 3 + y 3 + z 3 = x y z x 3 + y 3 + z 3 − 3 x y z + 3 x y z = 2 ( x 2 + y 2 + z 2 − x y − x z − y z ) ( x + y + z ) ( x 2 + y 2 + z 2 − x y − x z − y z ) + 3 = 2 2 0 + 3 = 1 3 .
Expanding x y z , we get
x y z = 2 x 2 + 2 y 2 + 2 z 2 − 2 x y − 2 x z − 2 y z (1)
Then,
x 2 y z = 2 x 3 + 2 x y 2 + 2 x z 2 − 2 x 2 y − 2 x 2 z − 2 x y z (2) x y 2 z = 2 x 2 y + 2 y 3 + 2 y z 2 − 2 x y 2 − 2 x y z − 2 y 2 z (3) x y z 2 = 2 x 2 z + 2 y 2 z + 2 z 3 − 2 x y z − 2 x z 2 − 2 y z 2 (4)
Now, notice that if we add equations (2), (3), and (4) together, we get
x × x y z + y × x y z + z × x y z
= ( x + y + z ) ( x y z )
= 2 0 x y z (according to the first equation we are given)
on the left hand side. Now, after adding the right hand side of equations (2), (3), and (4) together and cancelling like terms, we get
2 0 x y z = 2 x 3 + 2 y 3 + 2 z 3 − 6 x y z
2 6 x y z = 2 x 3 + 2 y 3 + 2 z 3
1 3 x y z = x 3 + y 3 + z 3
1 3 = x y z x 3 + y 3 + z 3
x + y + z x y z = ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 = ( x − y + y − z + z − x ) 2 − 2 ( ( x − y ) ( y − z ) + ( x − y ) ( y − z ) + ( y − z ) ( z − x ) ) x y z = − 2 ( x z + y z + x y − x 2 − y 2 − z 2 ) [ 1 ] ( x + y + z ) 3 = ( x + y + z ) ( x + y + z ) 2 x 3 + y 3 + z 3 + 3 ( x y ( x + y ) + x z ( x + z ) + y z ( y + z ) ) + 6 x y z = 2 0 ( x 2 + y 2 + z 2 + 2 x y + 2 x z + 2 y z )
Apply [ 1 ] to the right-hand side of the equation and the equation x + y + z = 2 0 to the left.
x 3 + y 3 + z 3 + 3 ( x y ( 2 0 − z ) + x z ( 2 0 − y ) + y z ( 2 0 − x ) ) + 6 x y z = 2 0 ( x z + x y + y z + 2 x y + 2 x z + 2 y z ) + 1 0 x y z x 3 + y 3 + z 3 + 3 ( 2 0 x y + 2 0 x z + 2 0 y z − 3 x y z ) + 6 x y z = 6 0 ( x z + x y + y z ) + 1 0 x y z x 3 + y 3 + z 3 = 1 3 x y z
Therefore,
( x 3 + y 3 + z 3 ) / ( x y z ) = 1 3
Expanding (x-y)^2 + (y-z)^2 + (z-x)^2 = xyz gives
2(x^2-xy-xz+y^2-yz+z^2)=xyz
Then multiplying the left side by (x+y+z) and the right by 20 since x+y+z=20 gives
2x^3+2y^3+2z^3-6xyz=20xyz
2(x^3+y^3+z^3)=26xyz
Therefore,
x^3+y^3+z^3/xyz = 13
(x^+y^3+z^3-3xyz)/xyz +3=(x+y+z)((x−y)^2+(y−z)^2+(z−x)^2)*1/2xyz +3=20xyz/2xyz +3=13
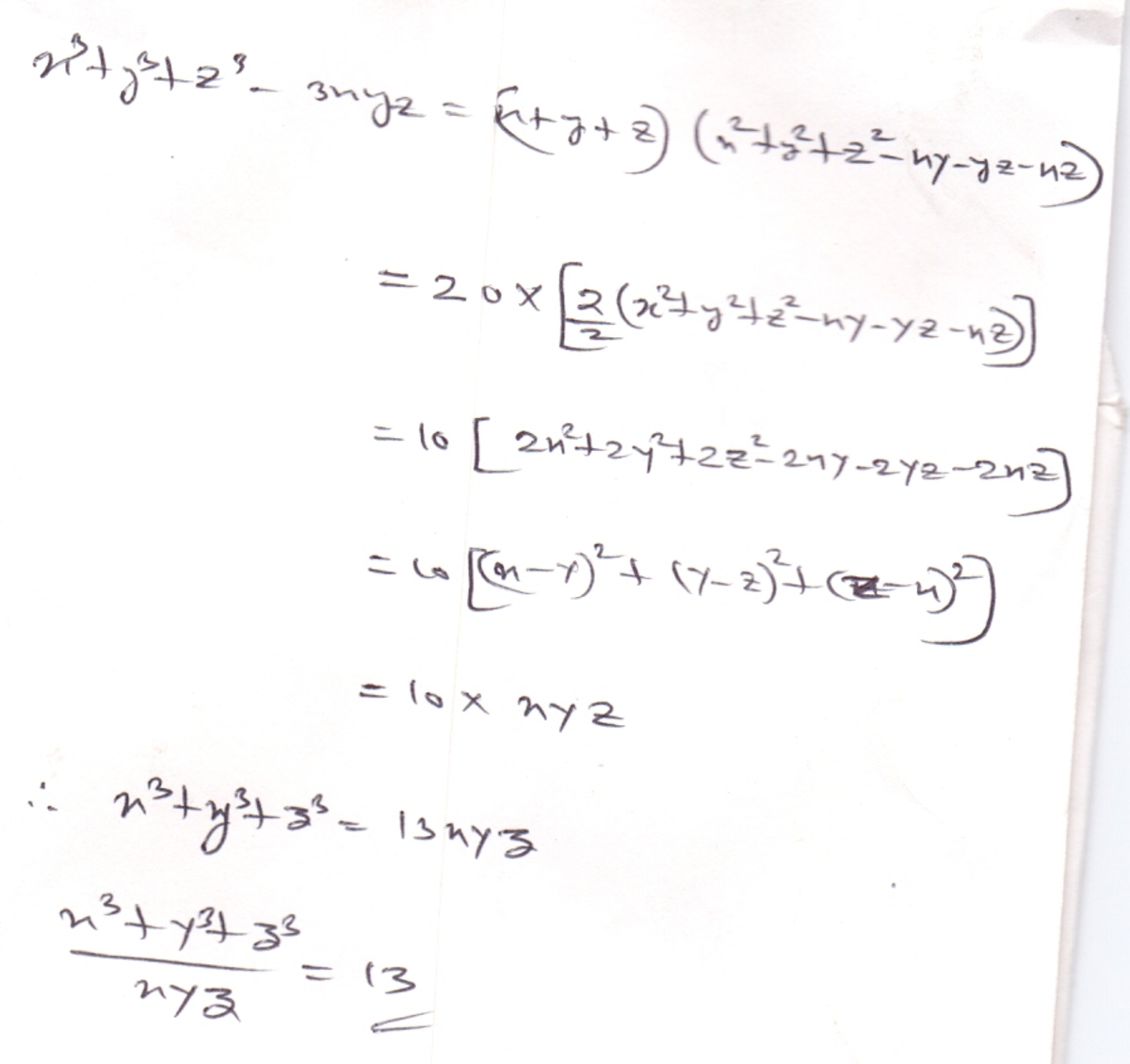
Since the given conditions, we have: ( x + y + z ) ( ( x − y ) 2 + ( y − z ) 2 + ( z − x ) 2 ) = 2 0 x y z . Or equivalently, ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x ) = 1 0 x y z . On the other hand, we have ( x + y + z ) ( x 2 + y 2 + z 2 − x y − y z − z x ) = x 3 + y 3 + z 3 − 3 x y z . Therefore, x 3 + y 3 + z 3 = 1 3 x y z and x y z x 3 + y 3 + z 3 = 1 3 .