I'm in Limbo
i i i . . .
For i = − 1 , the value of the infinitely nested exponent above is equal to A + B i for real values A and B .
Find the value of A 2 + B 2 to 3 decimal places.
The answer is 0.322.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
This solution is incomplete. It shows that if a solution exists, then it has to be of the form above. However, it doesn't show that such a solution must exist in the first place. We need to make an argument about limits, in order to be mathematically rigorous.
how did you got this A + B i e tan − 1 A B i from this e 2 − π B e 2 π A i
Log in to reply
No, it is from A + B i = A 2 + B 2 e tan − 1 A B i .
Log in to reply
This formula works only for positive A , though .
Log in to reply
@Otto Bretscher – It was positive. I made a mistake.
Log in to reply
@Chew-Seong Cheong – Can you please tell how did you find the value A using numerical methods?
Are you sure that i i … = i ? If so, then you are saying that i i = i , which is not true.
For complex exponentiation, the powers are identical doesn't mean that the bases are the same. For example, we have ( − 1 ) 2 = 1 2 but − 1 = 1 .
Log in to reply
Thanks for the comments. I was trying to fit in the answer. But now I got A = 1 and B = 0 . I wonder if it is right.
Log in to reply
It is not true that i i … = 1 either. If so, then i 1 = 1 , which is not true.
FYI: The answer should be 0.322.
Log in to reply
Sir,Could you please explain the solution?
Log in to reply
Anandhu, I have provided an explanation. See my solution above.
I believe A is positive. Luckily, your sign error does not affect the final answer ;)
Can you prove that h ( z ) converges only when e − e ≤ x ≤ e e 1 ?
Log in to reply
https://en.wikipedia.org/wiki/Tetration#Formal_definition
https://math.stackexchange.com/questions/1089458/how-can-i-prove-the-convergence-of-a-power-tower
We will use the principal value of complex logarithms throughout, with the imaginary part being on the interval ( − π , π ] . We need to solve the equation i z = z , or, e ( ln i ) z = z , or, e 2 π i z = z , or, z e − 2 π i z = 1 . If we make the substitution w = − 2 π i z , the equation becomes w e w = − 2 π i . Unfortunately, the equation w e w = x cannot be solved in closed form (not even for real x ) unless we use a special function, the Lambert W function in this case, defined by W ( x ) e W ( x ) = x . We find that w = W ( − 2 π i ) and z = π 2 i W ( − 2 π i ) ≈ 0 . 4 3 8 3 + 0 . 3 6 0 6 i . Thus the answer is ≈ 0 . 3 2 2 1 .
Write a comment or ask a question...thank u sir
Log in to reply
Comment or question about what? Give me a topic! ;)
Log in to reply
Comment or question about what? ANYTHING! I need more questions, 2 ain't enough!
Log in to reply
@Pi Han Goh – I have a job and a life, Comrades! My wife is jealous of "Brilliant" already ;)
Just wondering, can the value of A and B be written in a closed form ?
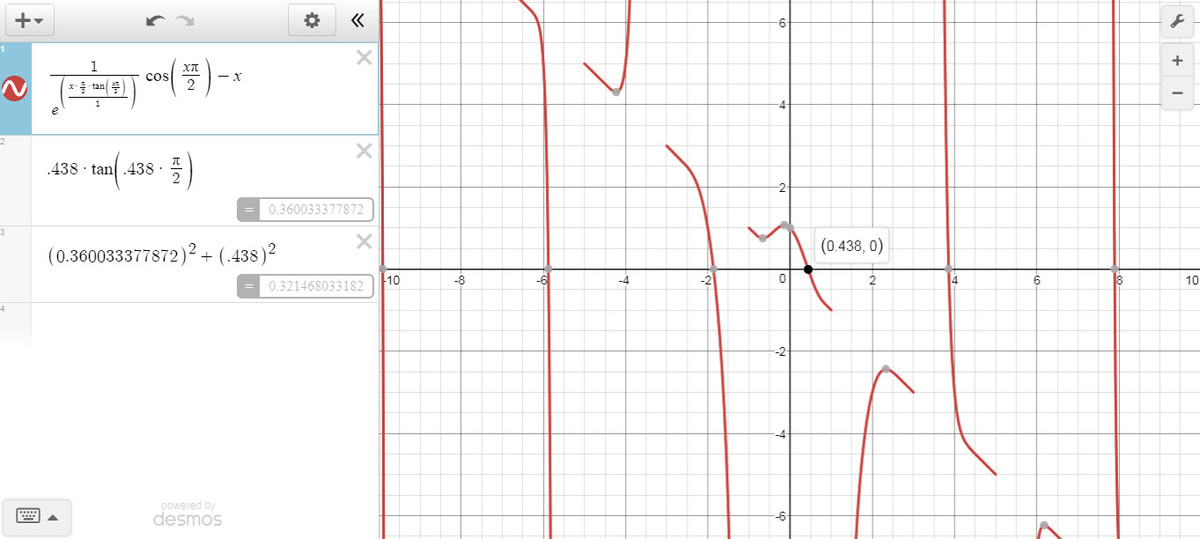 I had to use desmos to solve the pair of equations. I did the same way as
@Chew-Seong Cheong
. I am wondering is there any manual way to solve this pair of equation or do we have to take help of some graphing software.
I had to use desmos to solve the pair of equations. I did the same way as
@Chew-Seong Cheong
. I am wondering is there any manual way to solve this pair of equation or do we have to take help of some graphing software.
i i i . . . = A + B i = i A + B i ⇒ e 2 π i ( A + B i ) = e − 2 π B e 2 π A i = A 2 + B 2 e tan − 1 A B i
⎩ ⎨ ⎧ e − 2 π B = A 2 + B 2 2 π A = tan − 1 A B ⇒ A 2 + B 2 = e − π B ⇒ tan 2 π A = A B ⇒ B = A tan 2 π A . . . ( 1 ) . . . ( 2 )
Substituting Eqn. 2 in Eqn. 1:
A 2 + A 2 tan 2 2 π A = e − π A tan 2 π A
Using numerical method, we find that A = 0 . 4 3 8 2 8 2 9 3 7
⇒ B = A tan 2 π A = 0 . 3 6 0 5 9 2 4 7 2
⇒ A 2 + B 2 = 0 . 3 2 2 1 1 8 8 6 3
In response to the Master Challenger's question:
Thanks Otto Bretscher 's hint.
Infinite tetration of a complex number z is related to Lambert W-function as follows:
z z z z . . . = h ( z ) = − ln z W ( − ln z )
h ( z ) converges iff e − e ≤ x ≤ e e 1 ( 0 . 0 6 5 9 ≤ ℜ ( z ) ≤ 1 . 4 4 4 6 ) . Since A = 0 . 4 3 8 2 8 2 9 3 7 is within the limits, there is a solution for the problem.