Friendly High School
A senior class has 56 students and 15 activity clubs. It is known that if any 7 clubs hold a combined meeting of all their members, then there are at least n people in attendance.
What is the minimum value of n , such that we can conclude there must be (at least) one person who is in 3 or more clubs?
The answer is 41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I've a suspicion that the proof involves summing set sizes and their intersections. The total size of the Union of seven sets can be expressed as the sum of their individual sizes less the sum of the intersections plus some combination of 3 or more intersections. If no-one is a member of 3 sets these other terms must be zero.
Log in to reply
Yes, essentially you have to do some kind of counting argument involving ∣ A i ∩ A j ∩ A k ∣ = 0 .
Let me warn you against trying to do a general double-counting. The extrema condition only holds for a select number of sets, and the other "non-edge" cases give us too wide of a global bounding.
Log in to reply
As it turns out, a "general double counting" argument does work, once we did a bit more work. On average, every subset of 8 has close to 15 edges. There is only 1 subset of 8 with 0 edges, everything else has 7, 12, or 15 edges, in increasing density.
More accurately, my statement should have been "the direct general double counting doesn't really lead to any result as far as I can tell".
I think the question is incomplete. What if n = 1 and every person is a member of all the clubs? What is wrong with this?
Log in to reply
For such problems, you're always looking at the "worst case scenario that could exist", and not the "best case scenario that you can create".
Because of "we can conclude there must be ...", this means that "no matter what ever happens, there must always be such ....". So, taking your example of "When n = 1", it could be that the 15 clubs have 1 distinct member each, which would actually satisfy the condition for n=7. However, we cannot conclude that there must be one person who is in 3 or more clubs.
The answer is 1.
One lonely student trying to make friends by creating over a dozen activity groups which none of his 55 classmates join.
If he holds a "meeting" for any 7 of these clubs he will be the only guy and we can clearly conclude that he must be a (well, the) member of all 7 (and, by extension, 3 or more).
The minimum value for n is 1. Anything less would make it impossible for at least 1 student to be in any clubs.
Gonna go sing some Three Dog Night now.
Log in to reply
For such problems, you're always looking at the "worst case scenario that could exist", and not the "best case scenario that you can create".
It is possible to create a scenario where n = 1 is satisfied, but we cannot conclude that there must be at least 1 person who is in 3 or more clubs. E.g. having 15 people belong to 15 different clubs.
If 15 kids belong to 15 clubs then n would be 7 and we could not prove that one student was a member of three clubs. That means n = 7 is the wrong answer. But if n = 1 then one student must belong to at least 7 clubs. 7 >= 3.
Log in to reply
But if n = 1 then one student must belong to at least 7 clubs
That claim is not true. The question only tells us that " for any 7 clubs, there is at least 1 person in attendance". It does not imply that "There exists 7 clubs which have a combined meeting of exactly one person". Does this make sense now?
Note: The construction of "15 kids belong to 15 distinct clubs" still satisfies the condition for n=1, since any 7 clubs would have 7 people in attendance, which is at least 1.
We were looking for the MINIMUM value of n, being the sum of unique attendees from any seven clubs (of non-uniform club sizes). Clearly, if only one person showed up in the 7 clubs, we must conclude that person is a member of at least three clubs because that person is the solitary member of each of the seven.
In a sense, I am wondering if the problem is really is "what is the MAXIMUM number of attendees where by we CANNOT conclude there is someone who is a member of 3 or more clubs?" No, that doesn't work either, because you could have 56 show up, and the membership count is (56, 4,4,4,4,4,4) with no one being a member of 3 clubs.
The corner case is one club with 56 members, and 14 other clubs with non-overlapping memberships of 4. Another corner case is one club of 56, another club of 43, and 13 clubs of one member a piece. (No where did it say a club had to have at least two people.).
If the membership of 7 clubs attend and there are only 1, 2, or 3 people, you would have to conclude at least one of them belonged to 3 or more clubs. If 4 people attended out the seven, you could not make that conclusion.
Log in to reply
I'm having difficulty trying to understand what you are saying. I think you are making the following points
-
Claim that the answer n satisfies the condition "There is some allocation of clubs and members, such that there are 7 clubs with exactly n members, and there is one person who is in 3 clubs (not necessarily these 7 clubs).
-
Claim that the answer n satisfies the condition "The maximium n such that there is some allocation of clubs and members where every meeting has n members, such that we cannot conclude there is a member of 3 or more clubs.
-
Claim that (56, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4) and (56, 43, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1) are corner cases
-
If the meeting of 7 clubs only have 1, 2, or 3 people, then there is at least one person who belonged to 3 or more clubs.
If so, here are my comments.
-
I agree with this version that I wrote. Note that it does not imply "For all allocation of clubs and members where there is at least one person in 3 clubs, then there are 7 clubs with exactly n members". For a counterexample, place everyone in every club, then the meeting will have 56 members.
-
Close, but not quite. The answer would be the "maximium n + 1 ". IE My construction gives the "maximium n = 40 where we cannot find a person in 3 or more clubs", and the answer is 41. I could not make sense of your counter example, as you only have membership in 7 clubs, not all 15 clubs. If we take (56, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4) as the membership, note that there are 7 clubs whose meeting is (at most) 28, and hence the n that you calculate is 28, which is lower than my 40 (thus not a counter example)
-
It's not clear to me why they are corner cases. Can you clarify what makes them a corner case?
-
Yes, that is a true statement (esp if clubs were not allowed to have 0 members). However, that is not relevant to the problem as yet.
Log in to reply
RE: corner cases: The problem is looking for the minimum n that we would have to conclude at least one person was a member of 3 or more clubs. In the "corner case" where club member ship is (56, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4, 4), I.e. Everyone is a member of one club, but those 56 are each a member of one of the 14 other clubs, with no overlap among the 14, then we have a case where no one is a member of three or more clubs. If one of the seven clubs that assemble includes the 56 member one, then n=56 is insufficient to conclude that at least one member belongs to three clubs.
The problem fails because the clubs do not have to be close to equal sizes. The clubs do not even need to be at least two people.
Definition of Corner Case from Wikipedia: "In engineering, a corner case (or pathological case) involves a problem or situation that occurs only outside of normal operating parameters—specifically one that manifests itself when multiple environmental variables or conditions are simultaneously at extreme levels, even though each parameter is within the specified range for that parameter. "Corner cases form part of an engineer's lexicon—especially an engineer involved in testing or debugging a complex system."
Log in to reply
@Stephen Rasey – Yes, I know the definition of a corner case.
As I was explaining, your example gives us a corresponding value of n = 2 8 , which is much lower than the existing example of n = 4 0 . Hence, I would not consider it a corner / edge case. A corner case shouldn't just be "I came up against this artificial limit that I set myself". Instead, it should be "I came up against the limit set in the condition, and there is no clear way to improve this further". E.g. in your scenario, one way to improve it is to allow for the groups to intersect each other.
I would consider another construction that gave n = 4 0 (or even better, n ≥ 4 1 ) as an edge case to look into, and try to deconstruct the conditions that lead to the maximality.
Hope this clears it up. If not, let me know what is confusing / what you disagree with.
Log in to reply
@Calvin Lin – \ As I was explaining, your example gives us a corresponding value of n=28, which is much lower than the existing example of n=40. // No. If 29 show up at the combined meeting, all we could be sure of is that the membership of at least one of the seven clubs has a membership count between 5 and 29. We could not conclude there must be at least one person who was a member of at least 3 clubs.
Log in to reply
@Stephen Rasey – Precisely!
That is why your n=28 is not an edge case. We can construct a scenario where n = 29, but there isn't a person who is a member of at least 3 clubs.
On the other hand, n=40 is the edge case.
Do you think using a rank 3-tensor could clarify the problem? That is, a tensor T(i,j,k) | i exist (1,2,3,4,5,6,7), j exist (1,2,3,4) k, exist (1,2). To guarantee there's at least one student in three clubs at the meeting we must select one set of intersecting (1,1,k), (1,j,1) and (i,1,1) columns which gives a total of 7 + (4-1) + (2-1) = 11 students **. It's then a matter of selecting non intersecting columns of the form (T(a,b,k) | a xor b = 1) from the remaining clubs with the minimum number of members, those being 4 clubs who intersect with the initial 3 selected clubs which contain 2 members finally giving us 11 + 4(2 - 1) = 15 total students.
**Note: student T(1,1,1) is the student in this configuration which belongs to three clubs.
Not exactly rigorous and I suspect I'm wrong. What do you think? If you see a flaw, can you enlighten me to that flaw?
I just realized that this would represent 7(2) + 2(4) + 4(7) = 50 different clubs. Far more then requested. Is the composition of clubs outside the 7 selected relevant?
Log in to reply
I don't understand what your columns represent, or what T ( i , k , k ) is intended to refer to. If you define the terminology that might help clarify what you're going for.
At first, I was convinced the answer was 3 because I was confused by the wording "if any". I thought the question was asking, "among all the sets of 7 combined groups, pick one set that will give you the smallest n". I did not read it as all sets of 7 groups. 41 makes much more sense now.
If N = 50 then we can have distribution something like this. 7,7,7,7,7,7,8,8,8,8,8,8,8,8,8. (N=50 From first 7 groups)
Let's assume that from one of the group of 8, the students are in another group symmetrically.These 8 students are in just 2 groups.
Now if similarly all groups with 7 have a symmetry partner we can fill another 6 groups with a student remaining in each of them.These 42 students are also in only 2 groups.
Now we have 6 groups with a student less and 1 empty group.Also we have still 6 unused students. If we try to allocate these students in 2 groups each we will find that we have 2 places still to be filled and each student has used it's 2 groups quota. Thus someone (in this case 2 students) must have to go in his 3rd group. Thus the answer should be 50.
Now let N=49 then we can assume the distribution as 7,7,7,7,7,7,7,7,7,7,7,7,7,7,7 We cannot enforce from this situation that someone has to go in 3 groups. We can easily achieve this configuration with 49 players in 2 groups and 7 players in one groups.
Log in to reply
I have no idea what you are trying to say.
Are you trying to prove that N > 4 9 ?
When you say "Now let N=49 then we can assume the distribution as 7,7,7,7,7,7,7,7,7,7,7,7,7,7,7"", in order for "any 7 clubs to have 49 people in a meeting", it requires that "any 7 of these clubs have no members that belong in 2 or more clubs". If so, do you see why this would require 1 5 × 7 = 1 0 5 people and not just 56 people?
If instead, what you are saying is, create the 56 elements of { 1 , 2 , , 3 4 , 5 , 6 , 7 } ∪ { ( i , j ) ∣ 1 ≤ i , j ≤ 7 } , where the clubs are "first 7 people" and "7 clubs where i is fixed" and "7 clubs where j is fixed}, note that we can pick 7 clubs where there is a mix of the "fixed i" and "fixed j" sets, which give us less than 49 people. In fact, we can have 7 clubs with an meeting size of 3 × 7 + 4 × 4 = 3 7 , so your construction only gives us N > 3 7 .
Calvin, I don't know what you mean by "worst case" or "best case." The question asks for a minimum and the minimum possible value for n is 1.
Log in to reply
You are asked for the minimum value of n , such that **we can (always) conclude there must be ...". IE Even in the worst case scenario, there is a person that satisfies the condition.
What you're saying is "I found the minimum value of n , such that in this 1 very particular scenario, I can find 1 person that belongs to the clubs". IE This is the best case scenario, and we're living the dream.
Does this help clarify?
I think the solution is: April Fools. The problem is badly stated and insufficiently constrained.
Because one potential state is one club of 56 and 14 clubs of 4 with non overlapping members, Then it is possible to have 56 people show up from a combined 7 clubs and still not be able to conclude that at least one member must belong to three clubs.
On the other hand, not every one of the 56 belongs to ANY club. That's possible too. So if any arbitrary seven clubs show up, you can conclude that at least one person belonged to three or more clubs if the total attendance of the 7 clubs was 1, 2, or 3 -- and still you could only make that conclusion if at least one member from each of the seven clubs was in attendance.
Log in to reply
Because one potential state is one club of 56 and 14 clubs of 4 with non-overlapping members,
Note that in this case, we only have n = 2 8 , because there are some 7 clubs which have a meeting of 28 people.
The problem does not state "Such that there exists 7 clubs whose meeting has at least n people". The problem states "For any 7 clubs, the meeting has at least n people". Do you see the difference in these statements and how they affect thinking through of the problem? Let me know if this isn't clear to you.
I've fleshed out the complete solution. You can take a look at it.
Log in to reply
The phrase "For any 7 clubs...." means ANY (unknown) combination of 7 clubs. Not that there exists one set of 7 clubs where there is lower n. That being the case, because one of the clubs could have 56 people and , each of which belonged to only 1 other club, all the other clubs had 4 or fewer then then 56 is an insufficient number to conclude at least one person was a member of three or more.
The problem was insufficiently defined and constrained.
Log in to reply
@Stephen Rasey – After rereading, it seems like you are interpreting "if any 7 clubs hold a combined meeting of all their members" as "for some specific set of 7 clubs that I get to choose...". Do you agree? If so, would it be better if I rephrased it as " for every collection of 7 clubs that hold a meeting, there are at least n people in attendance"?
" means ANY (unknown) combination of 7 clubs". Perfect! We need it to be true for any unknown combination, not just for a given combination that we choose.
In the scenario where there is " one of the clubs could have 56 people, each of which belonged to only 1 other club, and all the other clubs had 4 people", then all that we can say is "for any 7 clubs that hold a combined meeting, then there is at least 28 people in attendance".
In particular, we cannot say "any 7 clubs that hold a combined meeting, then there is at least 28 people in attendance". We could say "there are some specific set of 7 clubs whose meeting would have 56 people in attendance".
Ok, at first I was thinking it was n=1, and worked on it for awhile there, and then I realised what Calvin has been trying to tell us.
If we assume that n=1, then that means that we can say "At least 1 person will be in attendance". BUT it's not the conclusive answer, because saying that doesn't mean it's proof that there's someone in 3 or more groups.
Let's say we have a fairly normal distribution of everyone in each group; there's at least 3 or 4 people in each one. We can STILL say "At least 1 person will be in attendance if any 7 groups meet together" - and that is why it's not proof that there's at least one person in 3 or more groups.
That said, the question is worded somewhat confusingly, and it's easy to understand why there's confusion on the matter. This is probably more of an issue with the English language than with the actual logic/math of the posited problem itself.
Log in to reply
I do not believe there is an issue with the English. I agree that the sentence structure requires careful deconstruction to ensure that we have indeed the correct interpretation of the problem.
If you think the issue is with the English (rather than deconstructing the logic), can you let me know which specific phrases you think are confusing, and what your interpretation of them is? This will allow us to improve the problem for everyone.
Edit: In particular, are you interpreting the phrase of "if any 7 clubs hold a combined meeting, then there are at least n people" as "there is some collection of 7 clubs whose meeting has at least n people", or do you read it as "given any (random) collection of 7 clubs, when they hold a meeting there will be at least n people"?
This is not a complete solution, but indicates where I think the proof should go.
Suppose no student belongs to three clubs. There is no point in a student not belonging to two clubs - if we have a student that does, just sign her up for any other club. Doing so will certainly not decrease the minimum turn-out for any seven clubs, and so can only increase the least possible value of n .
So, if every student belongs to exactly two clubs, we have a graph with 1 5 vertices (one per club) and 5 6 edges (one per student, and the vertices of each edge are the clubs that student belongs to). Note that 5 6 = ⌊ 4 1 × 1 5 2 ⌋ .
I think that the maximum least possible turnout for seven clubs will occur if this graph is triangle-free. There are plenty of examples of how to replace a graph containing a triangle with another one with at least the same minimum turnout for any set of seven clubs:
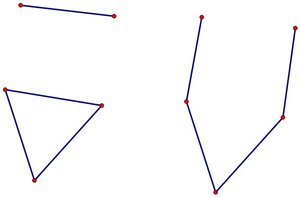
What I have not been able to prove that that it is always possible to find a set-up like the one above in a graph containing a triangle. I feel pretty sure that containing a triangle is an inefficient way of having the students join up - having three students with one belonging to precisely two of three clubs seems an arrangement that can be improved on. It is up to someone to justify this, perhaps...
If this is true, then we are looking for a triangle-free graph, and Turan's Theorem tells us that the graph must be the ( 8 , 7 ) -bipartite graph. It is easy to calculate that the minimum seven-club turnout for that graph is 4 0 , which makes n = 4 1 .
First, I will explain why the answer is at least 41, by providing a counter example when n = 4 0 .
Consider a 7 × 8 grid (7 rows, 8 columns). Let each cell represent a distinct person.
Let each row and column represent 1 club, giving us a total of 7 + 8 = 1 5 clubs.
Notice that everyone is in exactly 2 clubs, and that no one is in 3 or more clubs.
Given any 7 clubs, if they correspond to c columns and 7 − c rows, then there will be 7 × c + ( 8 − c ) × ( 7 − c ) = c 2 − 8 c + 5 6 = ( c − 4 ) 2 + 4 0 people in these 7 clubs.
Hence we have a construction where every 7 clubs have at least 40 people, but no one is in 3 or more clubs.
Now, let's explain why if every 7 clubs have at least 41 people, then there is one person in 3 or more clubs.
Proof by contradiction. Suppose that everyone is in at most 2 clubs.
First, the langugage of the problem doesn't allow us to easily manipulate it, so I'm going to translate it into the language of graph theory. (This isn't necessary, but I prefer to do so in general.)
Before we construct the graph, let's first ensure that everyone is in exactly 2 clubs, by forcibly subscribing them into any additional clubs as required. Now, consider the multi-graph G of 15 vertices that correspond to the club, and 56 edges that are connected for every person that belongs to both clubs. (Note: The reason for a multi graph, is that there could be 2 people who belong to the same 2 clubs. The reason for forcing everyone into 2 clubs, is to allow us to deal with proper edges instead of self loops).
In this language, the condition of "any 7 vertices are connected to at least 41 edges" is hard to define / describe, because they connect both inside and outside of the set (IE we can't bound the sum of the degrees of these vertices). Instead, the complement is easier to deal with, and has a simple idea: Any subgraph of 8 vertices has at most 5 6 − 4 1 = 1 5 edges .
Now, take any vertex. Consider the subgraph on the remaining 14 vertices. There are ( 8 1 4 ) possible subgraphs of 8 vertices, each of which have at most 15 edges. However, each edge will be double-counted ( 6 1 2 ) times. Thus, the number of edges in these 14 vertices is at most ( 6 1 2 ) ( 8 1 4 ) × 1 5 = 4 8 . 7 5 . Hence, the degree of the vertex, is at least 5 6 − 4 8 = 8 .
This is true of any vertex, thus the number of edges, which is equal to the sum of all degrees divided by 2 (due to double counting), which is at least 2 8 × 1 5 = 6 0 . This contradicts the fact that there are 56 edges.
Thoughts: This problem was hard to approach because