Simulating Dynamics - 2
Difficulty: Very hard indeed. To spoil it for you, only 18% of the attempts were right.
This problem is going to be pretty hard due to the many forces involved. The problem is similar to my previous problem, "Dynamic system with friction". Don't try to solve analytically.
However, the system this time is a pulley setup .
Consider the pulley system below as I have drawn, with a mass hung over a pulley hinge, providing a force to drag a block over to x = 0 (shown by the dotted line) solely using gravitational force. The string is completely massless, and only the floor has friction; all other surfaces are completely frictionless.
The pulley hinge is a vertical distance of 8 meters from the ground, and the length of the string is 1 4 meters.
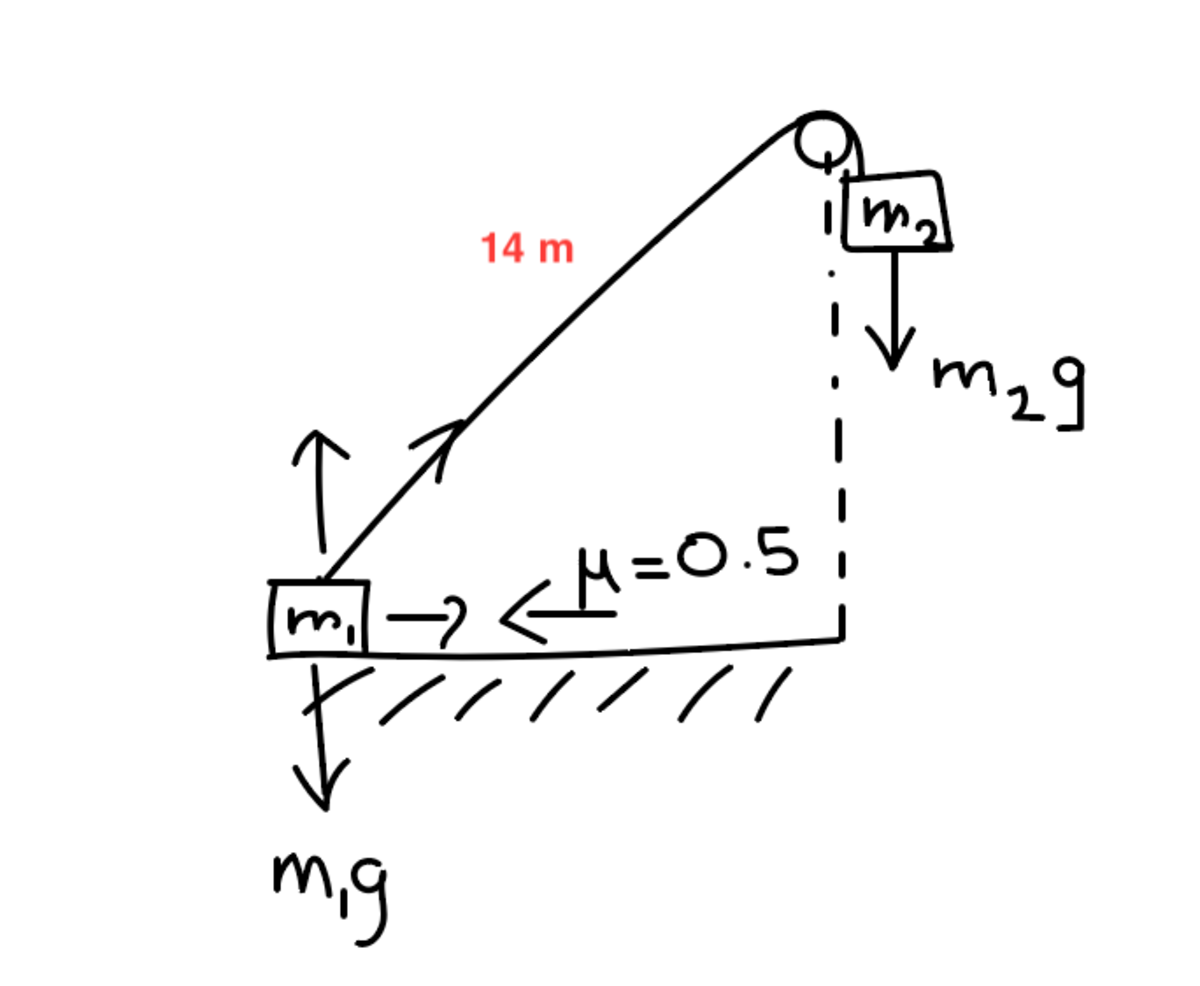
Block 2 starts at the hinge at time t = 0 seconds, and is also released at the same time. Block 1 is a distance of 1 4 meters away from block 2 diagonally and the displacement from x = 0 can be found using Pythagoras' Theorem.
Here m 1 = 3 k g and m 2 = 2 k g
There is a friction force acting opposite to the direction of the velocity, μ N , where N is the contact force between block 1 and normal to the floor. Here μ is the frictional coefficient, and is equal to 0 . 5 .
Find the time it takes for block 1 to reach x = 0 .
Take gravitational acceleration g to be 1 0 m / s 2 .
The answer is 3.865.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice one, I upvoted your solution. Your solution's getting a lot of upvotes. You're on a roll!
The equations of motion have been re-arranged in a matrix form in the solution. I have not necessarily used the same sign convention as you might have.
m 2 g − T = m 2 y ¨ T cos θ − μ N = m 1 x ¨ T sin θ + N = m 1 g
Finally, the constraint equation is:
x 2 + 6 4 = ( 1 4 − y ) 2
Double differentiation gives the fourth equation using which T , N , x ¨ and y ¨ can be solved for. I did that by re-arranging the equations in a matrix form.
θ = arccos ( 1 4 − y − x )
⎣ ⎢ ⎢ ⎡ m 1 0 0 2 x 0 m 2 0 2 8 − 2 y μ 0 1 0 − cos θ 1 sin θ 0 ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ x ¨ y ¨ N T ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ 0 m 2 g m 1 g 2 x ˙ 2 − 2 y ˙ 2 ⎦ ⎥ ⎥ ⎤
⟹ A ⎣ ⎢ ⎢ ⎡ x ¨ y ¨ N T ⎦ ⎥ ⎥ ⎤ = b ⟹ ⎣ ⎢ ⎢ ⎡ x ¨ y ¨ N T ⎦ ⎥ ⎥ ⎤ = A − 1 b
Uncommented simulation code attached below. Used the modified Euler step for numerical integration:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
|
Yup, looking back on it I think I had written out one of the forces wrong. I later got the same answer as you. Thanks for taking the effort to solve the problem😁
I cannot see your comments to my report without conceding the porblem. You may convey your thoughts here.
Log in to reply
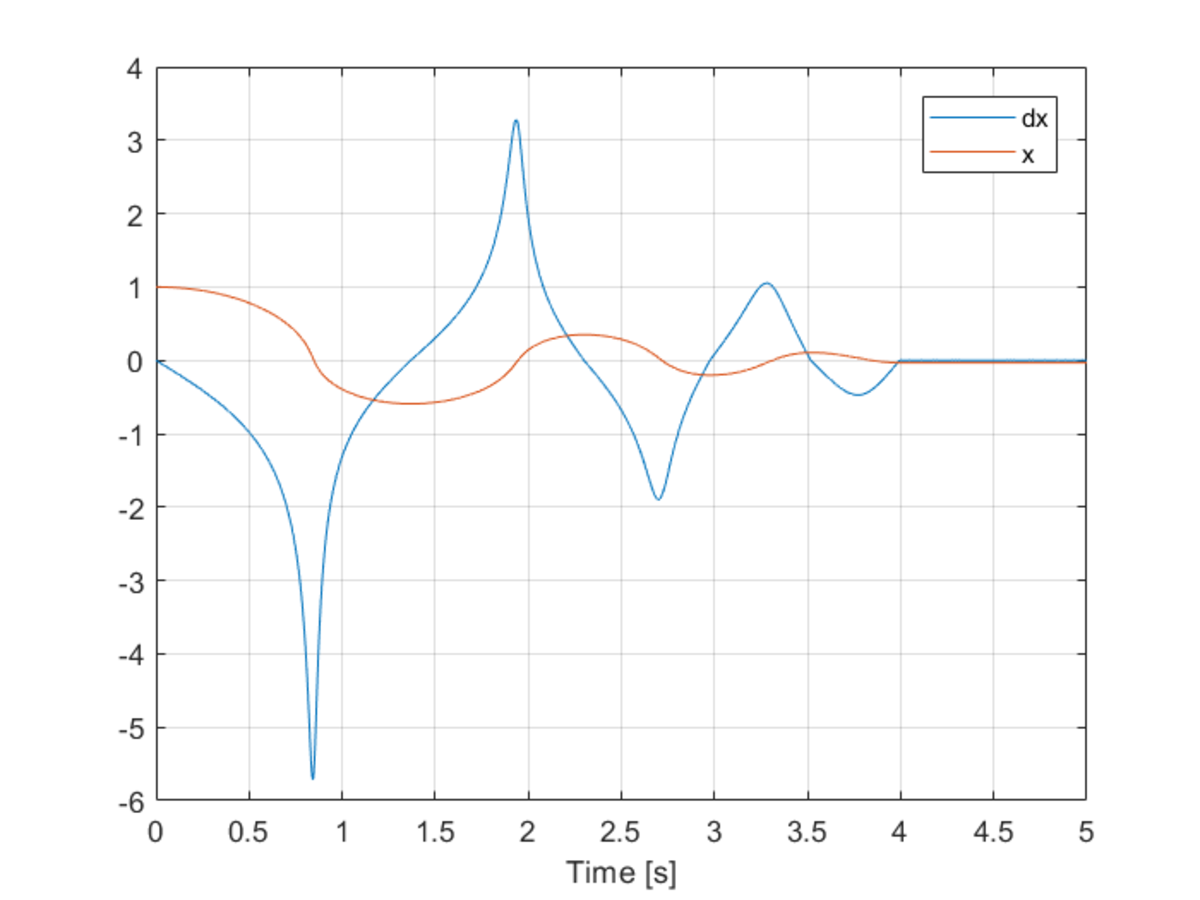
The variation of X coordinate and X component of velocity with time. This to me seems like a reasonable result.
Log in to reply
I noticed you have commented in the report for the problem. I cannot see them until I concede it. So please respond here, if you wish.
Log in to reply
@Karan Chatrath – @Krishna Karthik I noticed another comment on the problem report. Recall that I cannot see the comments.
Log in to reply
@Karan Chatrath – Oh hi, can you see this comment? :)
@Karan Chatrath – Ok; I have fixed up one of the errors in the code. I had first inputed the derivative of 3 x 2 incorrectly as 2 x in my code. It was incorrect originally. However, I still manage to get a different result from the one you have.
Log in to reply
@Krishna Karthik – Very well. In that case, delete that problem and re-upload it. The Brilliant staff will take time to update it.
@Krishna Karthik – I have verified my result with @Steven Chase . He gets the same result as I do. So please re-check your work. Perhaps later, I will share my approach too.
Log in to reply
@Karan Chatrath – I agree. I have re-uploaded the problem; I would like to see solutions so I can figure out what I did wrong, if that's ok and whenever you like.
Cheers!
Log in to reply
@Krishna Karthik – Yes, noticed that it is uploaded. I will post a solution after some time.
@Krishna Karthik – Have you tried using the atan2 function instead of atan? The atan function has ambiguities that can cause problems
Log in to reply
@Steven Chase – Ah, yes. I'll try that. I will reupload my problem right now.
@Steven Chase – The problem is re-uploaded now. Sorry for the delay. Cheers!
Is this Matlab code? Lol I'm only now learning how to use matlab. I'm actually finding it much better than python.
Log in to reply
Yes, this is MATLAB.
Log in to reply
Hey there; I've posted a discussion because I need help with a new problem. Is it ok if you can check it out? Thanks.
Just a different flavor of the solution posted by @Karan Chatrath . I have a 2 × 2 linear system to solve for T and x ¨ , so my expressions are correspondingly more complex than in the 4 × 4 linear system. Let the pulley height be h
The string length constraint gives (after a great deal of chain-ruling):
m 2 m 2 g − T = x 2 x ˙ 2 ( x 2 + h 2 ) − 3 / 2 − ( x x ¨ + x ˙ 2 ) ( x 2 + h 2 ) − 1 / 2
And the dynamics of the block with friction give the other equation ( θ is the angle between the string and the horizontal):
T cos θ − μ ( m 1 g − T sin θ ) = − m 1 x ¨
Solve the system for T and x ¨ on each time step, and use numerical integration. The block reaches x = 0 at approximately t = 3 . 8 7