Answer = 255

$x = \frac{243}{11}$ and $y = \frac{1}{11}$ ,

The polygon is divided into 5 triangles, each triangle's area can be calculated by using its 3 vertices by using Shoelace formula

• Area of (0,0) , (2,5) , (12,7) = |2x7 -12x5|/2 = $\color{#D61F06} 23$

• Area of (0,0) , (12,7) , (18,6) = |12x6 -18x7|/2 = $\color{#D61F06} 27$

• Area of (0,0) , (18,6) , (24,2) = |18x2 -24x6|/2 = $\color{#D61F06} 54$

• Area of (0,0) , (24,2) , (16,-6) = |-24x6 - 16x2|/2 = $\color{#D61F06} 88$

• Area of (0,0) , (16,-6) , (2,-8) = |-16x8 + 2x6|/2 = $\color{#D61F06} 58$

• Total Area = 23 + 27 +54 +88 + 58 = 250

Half of the area = 125

The traingle of area 88 must be divided into two triangles with areas $\color{#20A900} 21$ and $\color{#20A900} 67$

The first half = 23 + 27 + 54 + 21 = 125

The second half = 58 + 67 = 125

Area of (0,0) , (24,2) , (x,y) = | 24 y – 2 x |/2 = 21 -> gives $12 y - x = -21 \ (1)$

Equation of the line that connects (16,-6) and (24,2) -> $-y + x = 22 \ (2)$

Solve (1) and (2)

11 y = 1 then $y = \frac{1}{11}$ and

X = 22 + 1/11 then $x = \frac{243}{11}$

Disclaimer: This solution is wrong because I've hastily made the assumption that the image is accurate.

---

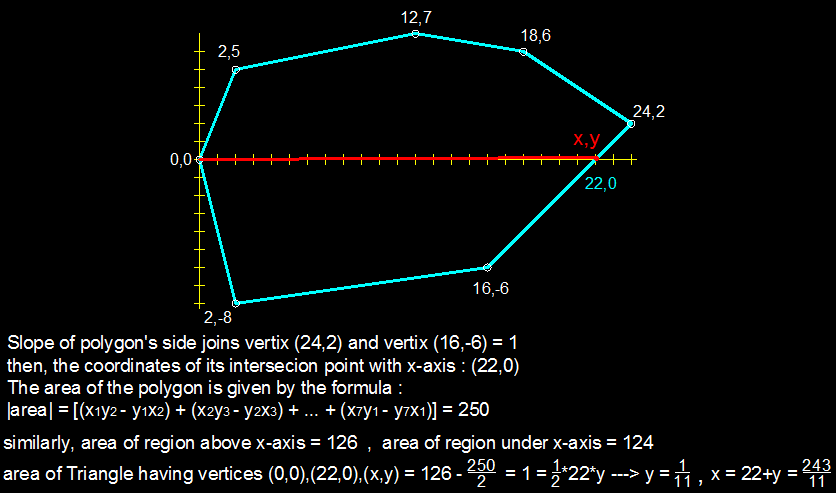
We that the area of a simple polygon with coordinates $(x_1, y_1), (x_2, y_2) , \ldots (x_n, y_ n)$ arranged counterclockwise, then the area of this polygon can be computed using the generalized version of the Shoelace formula :

$A = \dfrac 12 \begin{bmatrix}{x_1} && {x_2} && {\dots} && {x_n} && {x_1} \\ {y_1} && {y_2} && {\dots} && {y_n} && {y_1}\end{bmatrix} .$

In this case, we have the two equal areas,

$\dfrac12 \begin{bmatrix}{0} && {x} && {24} && {18} && {12} && {2} && {0} \\ {0} && {y} && {2} && {6} && {7} && {5} && {0}\end{bmatrix} = \dfrac12 \begin{bmatrix}{0} && {2} && {16} && {x} && {0} \\ {0} && {-8} && {-6} && {y} && {0}\end{bmatrix} .$

Or equivalently,

$[ 0(y) + x(2) + 24(6) + 18(7) + 12(5) + 2(0) ] - [0(x) + y(24) + 2(18) + 6(12) + 7(2) + 5(0)] \\ = \\ [ 0(-8) + 2(-6) + 16(y) + x(0) ] - [ 0 (2) + (-8)(16) + (-6)(x) + y(0) ].$

Simplifying this equation gives ${\color{#3D99F6}{ 10y =23 - x}}$ .

Now we just need to find the equation of the straight line that passes through the points $(16,-6)$ and $(24,2)$ , which is

$\dfrac{y - (-6)}{x - 16} = \dfrac{-6-2}{16-24} \quad \Leftrightarrow \quad \dfrac{y+6}{x-16} = 1 \quad \Leftrightarrow \quad {\color{#3D99F6}{y = x-22}} .$

Solving these two equations (highlighted in blue) simultaneously gives $x =\dfrac{243}{11}, y = \dfrac1{11}$ .

For completeness, we need to show that this intersection point indeed cuts through the straight line that passes through the two points $(24,2)$ and $(16,-6)$ .

Let us denote the points $O = (0,0), A = (2,5) , B= (12,7) , C = (18,6) , D = (24,2) , E = (x,y) = \left( \dfrac{243}{11} ,\dfrac1{11} \right) , F = (16,-6), G = (2,-8)$ .

By denoting the symbol $m_{PQ}$ as the gradient of straight line that passes through points $P$ and $Q$ , it's trivial to show that

$m_{OA} > m_{OB} > m_{OC} > m_{OD} > m_{OE} > m_{OF} > m_{OG} ,$

hence the intersection point $E$ only cuts through the side $DF$ of this simple polygon.

And our answer is $243 + 1 + 11 =\boxed{255}$ .