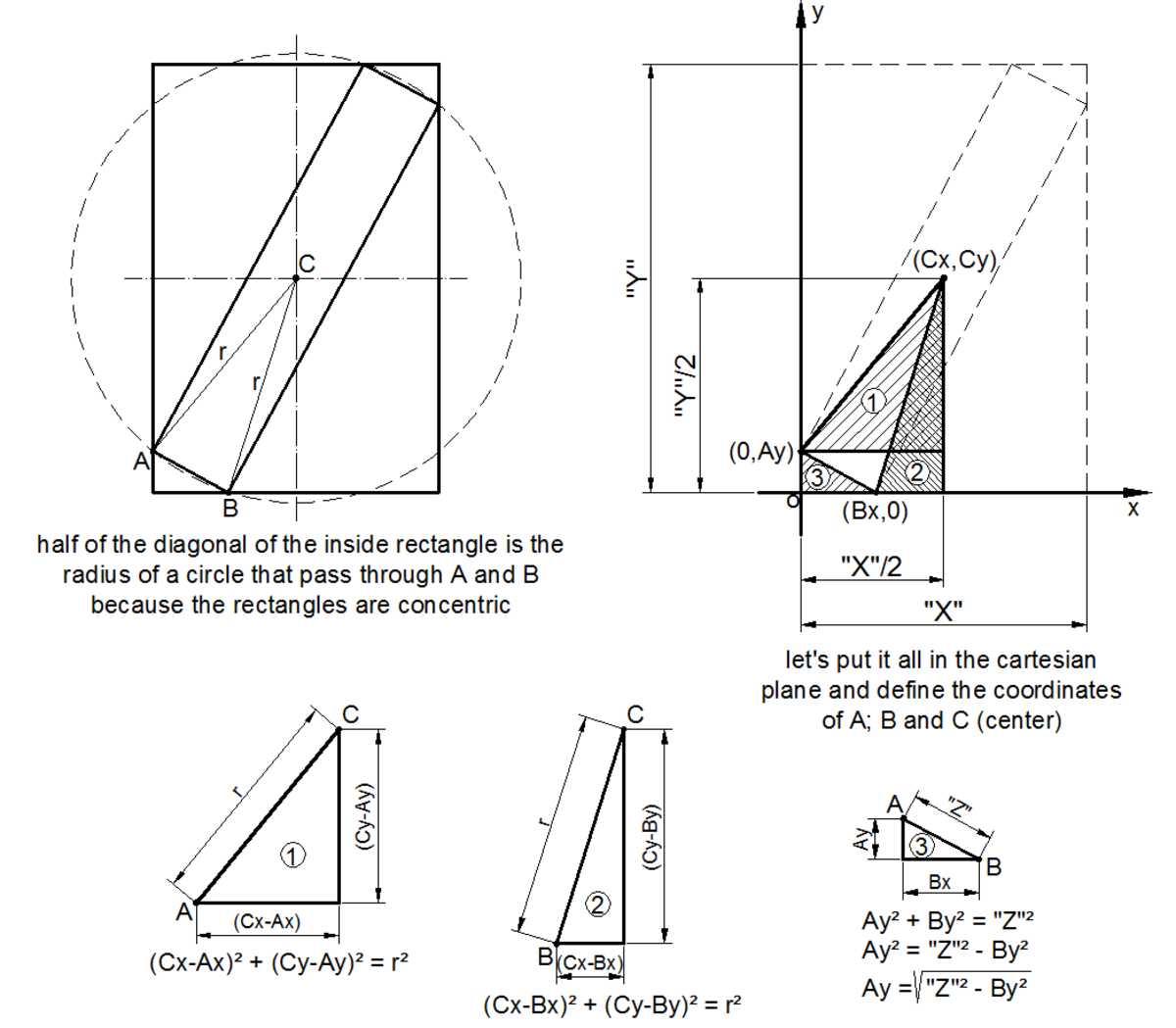
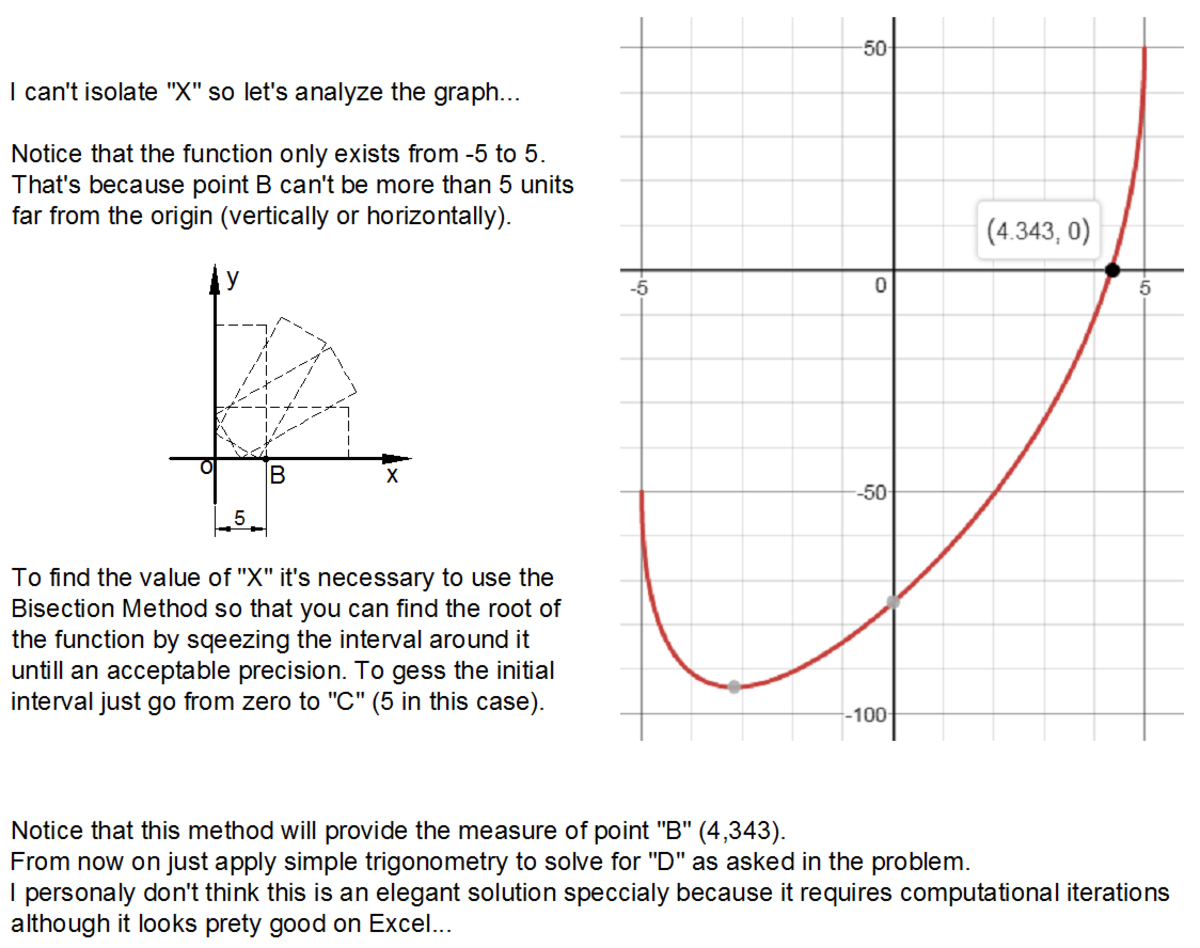
concentric rectangles
Given that
A
=
1
0
,
B
=
2
0
and
C
=
5
, what is the length of
D
?
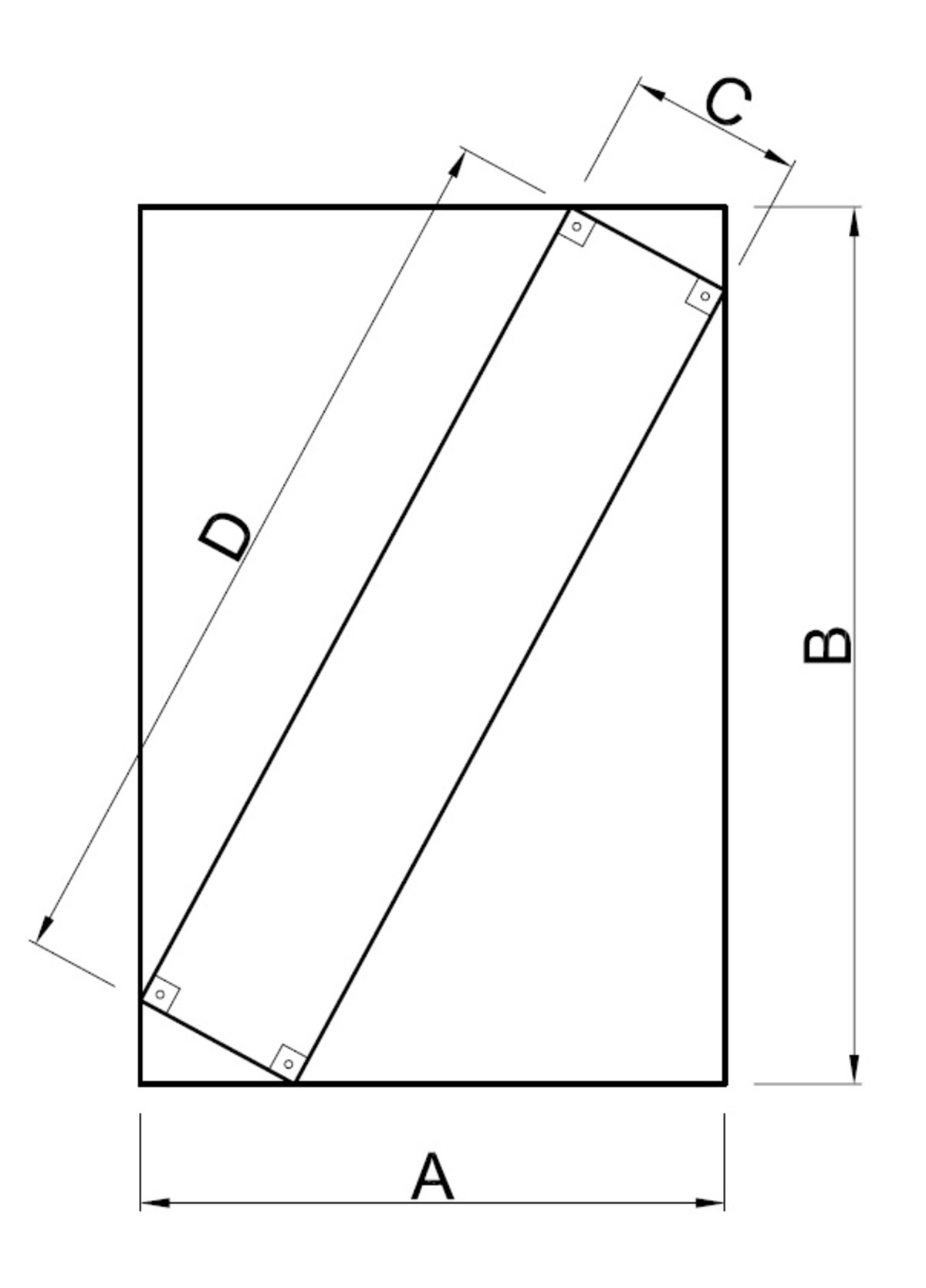
The answer is 19.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
[Nevermind this solution.I misread the problem(But still got it right?So lucky)]
The diagonal of the smaller rectangle = 2 0 2 + ( 1 0 − 5 − 5 ) 2 = 2 0 ,so D = 2 0 2 − 5 2 = 3 7 5 ≈ 1 9 . 4
sorry but it seems to me that you just got lucky... in fact i didn't understand your solution and i dont think it works for other values... can you try for the following examples...? (A=1234; B=5678; C=910; D=5634,86 (not 5573,9)) or (A=4321; B=8765; C=19; D=9757,17 (not 7647,3))...if you try it with some CAD software that allows parametrization you can check it...any way, I'll soon post what i consider to be a reasonable algebric solution and hope for you to share your comments...thank you.
Log in to reply
D = B 2 + ( A − 2 C ) 2 − C 2
Log in to reply
So..., it seems to me that there is a miss understanding about the picture because the measure “C” is not parallel to the measure “A”. In this case, your formula works as a good approximation. But if you plug in some big numbers the error will become noticeable. Let’s try some other values: A=98765 ; B=123456 ; C=45678 ... ((123456^2)+((98765-2*45678)^2)-( 45678^2))^(1/2)=114933,88 instead of 116465,17 that would be the exact value...
Log in to reply
@Nordau Luiz Palko Roberto Santos – Yeah,you're right.I misunderstood it as A//C.