Conceptual Physics: IV
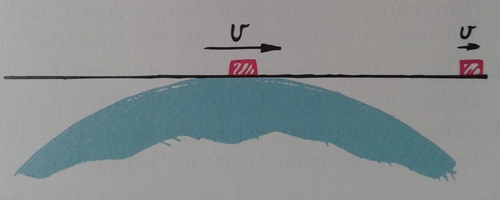Suppose an object is set sliding, with a speed less than escape velocity, on an infinite frictionless plane in contact with the surface of the Earth, as shown. Describe its motion. (Will it slide forever at a constant velocity? Will it slide to a stop? In what way will its energy changes be similar to that of a pendulum?)
A . The object will oscillate about the point of contact between the plane and the Earth's surface, sliding right, stopping, sliding to the left, stopping, and back again in a closed loop - just like a pendulum would if given an initial push.
B . Since the plane is frictionless, the object does not have to undergo any resistance to its horizontal motion unlike its terrestrial counterparts that have to move against the air resistance of the Earth's atmosphere. Hence, the escape velocity rules do not apply to the object, and the object will slide indefinitely - to infinity and beyond - just like a pendulum would swing in a circle inside a vacuum chamber.
C . The object will slide along the direction of its initial velocity, eventually to be pulled backwards until it passes its starting position. Then, the object will oscillate at the point somewhere between its starting position and its turning position - just like a pendulum would do starting with the highest velocity at the initial swing and then oscillating at the point between its starting position and its turning position.
D . The object will slide along the direction of its initial velocity, eventually to be pulled backward until it passes the point of contact between the plane and the Earth's surface. Then the object will again change directions, after sliding a lesser distance. This will keep happening until the object finally stops at that point in contact with Earth - just like a pendulum would eventually stop swinging and end up at its lowest point.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The reason why the girl moved forward is because when she was holding the ball, she had to lean back. When she let go, she moved forward to normal standing position. The physicist teacher should have realized this before the experiment was done, which makes me think he hasn't done this much, or has only done it with very heavy men. The girl acted embarrassed, but I was more embarrassed for the teacher, who should have known better.
Log in to reply
Log in to reply
O---kay, that was Miley Cyrus, wasn't it? Very funny.
This is gold, hahaha!
I'm just wondering if the "space roller-coaster" might lose energy gradually due to gravitational radiation, (i.e., gravity waves). We might also need to consider the conductivity of the object and its subsequent interaction with the Earth's magnetic field, as there is the potential for eddy currents dissipating the energy of the object. I took the same energy approach as you did and as a result chose (A), but there may be more to this (fun) question than first meets the eye. :)
P.S.. The girl did move her head forward a few inches. That must have hurt, (besides being a bit embarrassing) :(
Log in to reply
Nice!
You nailed the girl question. Well yeah of course this idea is obviously not feasible and this question is overly simplistic. The costs of sustaining such a "plane" would be enormous. If we are to use sling-shot method for roller-coasters, we need to come up with something else. But eventually, the number one thriller in the universe shall be singularity-coaster => where you ride around the event horizon of a black hole!!!
Log in to reply
Yeah, I guess that would be called the "Point of No Return" ride. :)
Just curious - what's with the #ApplePieAndCoffee hashtag?
Log in to reply
Log in to reply
@John M. – ...#theresahashtagforeverythingintheuniverse
Why the heck did someone give your reply a down-vote? Anyway, I don't know which is scarier - that equation you've linked to or the possibility that I could eat a spider while I'm sleeping tonight. :O
Edit: That's interesting; the down-votes on all your responses disappeared. Wonder what happened there; perhaps it was just a glitch that corrected itself.
Log in to reply
@Brian Charlesworth – Lol I just love how you pay attention to those details just like I do - not many people do the same.
Well, to be honest, I think you'll be the first to find out that the only problem there is to solve is the bottom end of the fraction -> the sum.
But if you figure out how to do the rest, I shall post the answer and the full solution - which I know Michael has been waiting for for so long (0r mayb3 n0t)
Cheers
I agree with you, Brian. There are other effects not mentioned here that should slow the oscillation down.
Log in to reply
This would be a good question to have a seminar on at an astrophysics convention; the discussion would be a lively one. :)
However, I would like to point out a very important difference between this example and usual pendulum. In the normal pendulum, the magnitude of force acting on the oscillating object is proportional to its distance from the origin. Here opposite happens! The force on the object actually decreases when it goes farther from the point of contact. Can you explain why still the pendulum argument holds?
Log in to reply
Hm?
Not sure what pendulum you're referring to, but an ordinary pendulum is only acted upon by a few major forces, including friction, air resistance, and gravity - and none of them involve proportional relationships in the distance from the origin of the bob.
Log in to reply
Please see my response to Math Philic.
Log in to reply
@Snehal Shekatkar – @John Muradeli What Snehal is pointing out is that a simple pendulum exhibits SHM , which by definition means, a force proportional and opposite to the displacement to the object. But that assumption requires a small angle approximation. We cannot do that for this problem obviously because it's on a planetary scale. So if we try to actually describe the motion we end up with an ugly second order differential equation . I think what Snehal is saying is that the pendulum analogy doesn't hold for this particular scenario. I still think energy is a good way of thinking about this.
Log in to reply
@Thaddeus Abiy – I completely agree with you that energy is a good way of thinking about it.
The differential equation can be solved but with approximation. If you have time to go through my and Snehal Shekatkar's conversation, you will find we have found the SHM argument to be valid. We have reached that without differential equation.
@Thaddeus Abiy – Thanks for the comment. You may want to correct my name by the way. ;-)
I couldn't get you. Could you explain a bit more?
By normal pendulum I guess you are talking about simple pendulum. If it is so, then the force acting on the oscillating object or the bob is proportional to its distance from the origin or equilibrium position only for small oscillations . To put it in other words: under the assumption that the amplitude of oscillations are small, the force acting on the oscillating object or the bob is proportional to its distance from the origin or equilibrium position . If you also take the similar assumption here, i.e. let the object in the question make small oscillation, then force on the object doesn't decrease when it goes further. Because for small oscillation distance between the object and earth center can be approximated to Earth's radius. Was this helpful? @Snehal Shekatkar
Log in to reply
No. Replace the word pendulum by linear harmonic oscillator so that no approximation is required. For harmonic oscillator, the force is proportional to displacement from the mean position. In this case however force decreases with increase in the displacement. Hence to me it is not very obvious that the motion must be like oscillator.
Log in to reply
@Snehal Shekatkar – What "force" are you referring to here? The total net force?
Log in to reply
@John M. – Only the component of gravitational force along the plane matters. I am referring to that component. Please see my response to Math Philic. I have written a differential equation there.
@John M. – Yes, the net force.
@Snehal Shekatkar – Now, that's the implicit insight the above solution has which we are failing to see.
We are sticking to Simple Harmonics...because it is easy to spot.
Wouldn't it be good if you just had a quick reference from a book about pendulums as oscillator?
Log in to reply
@Soumo Mukherjee – Perhaps I didn't get you here. So I know that there are things like non-linear oscillators and simple pendulum is one of them unless you keep its amplitude small. That is okay. My point is that "even though the restoring force in this case is smaller (not larger) when the object is displaced far from the mean position, the oscillatory motion happens" is not so obvious and though the energy principle that you wrote is fine, it is not clear how could particle be brought back if we don't have enough force for it to do so.
Let R be the radius of the earth and r be the distance of the particle from the center of the earth. Then we have x 2 = r 2 − R 2 , where x is the distance between touching point and particle at a given time. Hence the equation of motion in this case would be:
d t 2 d 2 x + ( x 2 + R 2 ) 2 3 α x = 0
Is it obvious for you that this equation gives oscillatory motion?
Log in to reply
@Snehal Shekatkar – Oh thanks for pointing that out.
But that was exactly what I was trying to clarify in my previous comments. Never mind. I was saying that if θ be the angle between r and x then if F be the Gravitational force at x , then its component along the plane(i.e tangential to its motion. Lets denote it be F x ) will be F x = R 2 G M m cos θ , where cos θ = r x . Now for small oscillations (i.e when θ is small) r ≅ R & cos θ ≅ R x . Hence we get this F x = R 2 G M m cos θ = R 2 G M m . R x .
Taking into consideration that displacement is opposite to acceleration F x = − R 3 G M m x = − k x . Am I wrong? @Snehal Shekatkar
Log in to reply
@Soumo Mukherjee – But where in the problem has it been mentioned that oscillations are small? In fact why do you think that if at all there is any oscillatory motion then it would be with small amplitude?
Log in to reply
@Snehal Shekatkar – My friend didn't I also tell you that above solution is insightful. By looking into the energy change, even without calculating the change, you can very reasonably predict that the motion is similar to the pendulum. Because changes in energy of the simple pendulum are similar to ours. Hope I am clear in this.
I think that the amplitude will be small because if it isn't small @Snehal Shekatkar , the pendulum itself wouldn't obey Simple Harmonic Motion. In every question that I have solved about Simple Harmonics Motion contained the phrase 'for small oscillations.' Did you get me?
Log in to reply
@Soumo Mukherjee – That's not a physics argument. Isn't it? In the first place, the motion may not be oscillatory at all if the amplitude is not small. One must solve that differential equation to see what the actual motion looks like. I will try to solve it numerically and will post the phase space trajectory here.
Log in to reply
@Snehal Shekatkar – No, it isn't a Physics argument. I know that.
Yes I agree with that for determining the motions you need to do that. And I also agree that if the question had mentioned that v is small or somehow indicated that the displacement made is small, it would have been more agreeable to the answer. But I said you can 'predict' it by observing the changes in energy. We both know that at initial stages of SHM we use arguments from Work-Energy. Its at a later stage that the form F=-kx comes into play. The above solutions is such that you even don't have to assume that the oscillations are small. Only use a more fundamental law of Nature.This is the implicit insight I am talking about.
Well you can very much solve the equation and find the trajectory and motion. I can do that too. But, come one pal, why are you sticking so much to one problem? There are lots more to solve out there. Moreover in the very beginning of the question we have a phrase, "...In what ways will its energy changes be similar to that of a pendulum?" It will consume more of your time Snehal Shekatkar . But if you want to post a full rigorous solution, you are always welcome. We will be waiting for you to upload it. :)
~Cheers!~
Log in to reply
@Soumo Mukherjee – How you even solve the differential equation? Wolfram alpha failed. @Michael Mendrin , @Math Philic , @Snehal Shekatkar
Log in to reply
@Thaddeus Abiy – Could you say which differential equation are you talking about?
Log in to reply
@Soumo Mukherjee – The ugly one.(from Snehal's comment)..I think it's a second order non linear ODE
Log in to reply
@Thaddeus Abiy – For small oscillation x is small compared to R so that you can neglect it and proceed, so that x+R approx to R. Just below that comment I have used the approximation.
@Thaddeus Abiy – I will look into this issue when I finish the appropriate chapter.
Thanks
@Thaddeus Abiy – Today I will find some time to solve that equation numerically. I will post the phase space trajectory then.
I didn't know that your are pursuing Phd in Physics. Hats off to Snehal. I am interested in research too. What's the real scenario in our country? From what I have read around internet, its not as good as other countries.
I have more questions for you. If you get any time plz reply to them. Did you also do your UG as well as graduation from IISER ? What about Maths? I have heard ISI and CMI are the best, what about IISER?? Is there any cutoff marks for IIT-JEE papers to get into IISER? 'm getting a bit excited now... I want to pursue higher education in Maths and also get into research. Any advice?
Log in to reply
Discussion would be long here. Can you create a new note about this topic and give link to me? Others would also contribute then.
Alright now that I've mastered pendulums and gravity - has the issue been resolved? I can answer the question if not.
Cheers
This problem tests the understanding of Conservation of Mechanical Energy
Since there is no friction and the object does not release internal energy, the two types of energies we are dealing with are Kinetic and Potential energies (K and U, respectively).
For simplicity, suppose the object starts right at the point of contact between the Earth and the plane. At this point, the object has a certain amount of Mechanical energy, M , which is the sum of its Kinetic and Potential energies:
M = K + U .
This Mechanical energy is conserved inside the Earth-object system since no external force acts on the system.
At the start, the object has maximum Kinetic energy. Then, as it slides, it begins to lose this Kinetic energy due to the pull of Earth's gravity. In turn, the object gains Potential energy with respect to the Earth 1 . Its Mechanical energy in time, from its initial position to the turning point, can be represented with sizes of letters, with larger indicating greater magnitude:
M = K + 0
M = K + U
M = K + U
M = K + U
M = 0+ U
The amount of kinetic energy lost equals the amount of potential energy gained. No external force is applied to the Earth-object system, and thus no net external work is done to change the total mechanical energy of the system.
When the object reaches its turning point, its kinetic energy is zero. Then, it reverses its direction of travel and begins to slowly regain its kinetic energy. The object's kinetic energy will be at its highest at the instant it crosses the point of contact between the plane and the Earth - where its potential energy is zero.
The same rules will apply when the object will slide toward the other direction, and thus the process will form a closed loop of the object sliding back and forth along the plane until the heat death of the universe (or until I eat the plane).
Note the similarities with the mechanics of the pendulum.
As the pendulum rises, it loses kinetic energy and gains potential energy. When its at the bottom, its kinetic energy is the greatest and its potential energy is zero.
[1 - Note that the initial position of the object does not make a difference in the object's overall behavior. Starting farther away from the point of contact between the plane and the Earth would simply mean greater total Mechanical energy. Since the object starts farther away, it has the same kinetic energy it would have had when starting in the middle; but now it also has the potential energy in addition to it. Another way to think about it is that if the object were to start off closer to Earth, by the time it would reach that different initial position, it would already have lost some kinetic energy.
So the overall effect is that it would swing at a grater radius from the middle, just like a pendulum would if given the same kinetic energy but starting above its lowest point.]
Can you tell why the girl was hit in the face?
But most importantly, can you tell why B , C , and D are wrong? To truly understand this problem, you must be able to explain why those choices are strictly wrong.
This contraption is the future of space roller-coasters!