Cone you sphere the time to solve this?

Calculus Level 3

If the largest possible volume of a cone inscribed in a sphere of unit volume can be represented as $\frac{a}{b}$ , where $a$ and $b$ are coprime natural numbers, what is the value of $a+b$ ?

The answer is 35.

2 solutions

Chew-Seong Cheong
Jul 25, 2015

Volume of a cone is given by: $V = \frac{1}{3}\pi r^2 h$ , where $r$ is the radius of the circular base and $h$ the height. For a cone inscribed in a sphere, for a fixed $r$ , the largest $h$ and hence the largest $V$ is when the cone is right circular.

Now consider a circle $x^2+y^2 = 1$ . Let the vertex of the cone be $(-1,0)$ and its base be parallel to the $y$ -axis, hence $r=y$ and $h= 1+x$ . Therefore, we have:

$\begin{aligned} V & = \frac{1}{3}\pi r^2 h = \frac{1}{3}\pi y^2 (1+x) = \frac{1}{3}\pi (1-x^2)(1+x) \\ & = \frac{1}{3}\pi (1 + x -x^2 - x^3) \\ \Rightarrow \frac{dV}{dx} & = \frac{1}{3}\pi (1-2x-3x^2) \end{aligned}$

$\begin{aligned} \frac{dV}{dx} & = 0 \\ \Rightarrow 1-2x-3x^2 & = 0 \\ 3x^2 + 2x -1 & = 0 \\ (3x-1)(x+1) & = 0 \end{aligned}$

Since $\dfrac{d^2V}{dx^2} \begin{cases} < 0, \text{when } x = \frac{1}{3} \\ > 0, \text{when }x = -1 \end{cases}$ , $V$ is maximum when $x = \frac{1}{3}$ .

$\begin{aligned} V_{max} & = \frac{\pi}{3} \left(1-\left(\frac{1}{3} \right)^2\right) \left(1+\frac{1}{3}\right) = \frac{\pi}{3} \left(\frac{8}{9} \right) \left(\frac{4}{3}\right) = \frac{32\pi}{81} \end{aligned}$

$V_{max}$ is from a cone inscribed by a $\color{#3D99F6} {\text{unit-radius}}$ sphere, therefore, the maximum volume of a cone inscribed by a $\color{#3D99F6} {\text{unit}}$ sphere is:

$V'_{max} = \dfrac{V_{max}}{\frac{4\pi}{3}} = \dfrac {\frac{32\pi}{81}}{\frac{4\pi}{3}} = \dfrac{8}{27} \\ \Rightarrow a + b = 8 + 27 = \boxed{35}$

Moderator note:

You have only shown that the extremal point of the volume occurs at $x=\frac13$ , but you did not show that it is a maximum point.

@Raj Magesh : NCERT type problem, eh?

Vishwak Srinivasan - 5 years, 10 months ago

Yeah, I like optimization. XD

Raj Magesh - 5 years, 10 months ago

Your title for this problem is very good! @Raj Magesh

Noel Lo - 5 years, 10 months ago

@Noel Lo – Haha, thanks. I try to be as punny as possible, though many want to strangle me for it. :P

Raj Magesh - 5 years, 10 months ago

External point? You mean the vertex or apex? $x$ is parallel to the base. The circle $x^2+\color{#D61F06}{z^2} = r^2$ is the base. $y=r$ the radius of the base. The vertex is at $(-1,0)$ , therefore the height $h = x - (-1) = 1+ x$ and volume $V=\dfrac{\pi r^2h}{3}$ $= \dfrac{\pi y^2(1+x)}{3}$ $= \dfrac{\pi (1-x^2)(1+x)}{3}$ . Therefore $V = V(x)$ a function of $x$ and maximum $V(x)$ occurs when $\dfrac{dV}{dx} = 0$ .

Chew-Seong Cheong - 5 years, 10 months ago

To show that it's maximum, use the second derivative test and show that $V_{\text{max}}''\left(\frac13\right) < 0$ .

Pi Han Goh - 5 years, 10 months ago

Thanks. Didn't notice it is "extremal". I thought it was "external".

Chew-Seong Cheong - 5 years, 10 months ago

Yeah, $\dfrac{dV}{dx}=0$ only implies that the point is either a point of maximum, a point of minimum or a point of inflection.

Raj Magesh - 5 years, 10 months ago

Yes, I missed that step of showing $\dfrac{dV}{dx} < 0$ . But actually, if you solve for $\dfrac{dV}{dx} = 0 \quad \Rightarrow x = \frac{1}{3}$ and $x= -1$ . When $x=-1$ , $V = 0$ minimum, $x = \frac{1}{3}$ $V$ is maximum.

Chew-Seong Cheong - 5 years, 10 months ago

@Chew-Seong Cheong – That's not enough proof, you have only shown that $V(0)$ and $V\left(\frac13\right)$ are EXTREMAL points, and not min/max points.

Take $y = x^3$ as an example. At $\frac{dy}{dx} = 0$ , does it mean that at $x = 0$ , it is min or max point? no! It's just an inflection point

Pi Han Goh - 5 years, 10 months ago

$p = \frac{\sin^2 \theta~(1 + \cos \theta)}{4}$

Maximum $p$ occurs at $\cos \theta = \frac13$ while $\sin \theta = \frac{\sqrt{8}}{3}:$

Maximum $p = \Large \frac{\frac{8}{9} (1 + \frac13)}{4} = \frac29 \frac43 = \frac{8}{27} = (\frac23)^3.$

8 + 27 = 35

Answer: $\boxed{35}$

Lu Chee Ket - 5 years, 4 months ago

May you elaborate your solution.

What is p here? How did you reach to it? Thanks.

Pulkit Gupta - 5 years, 3 months ago

@Chew-Seong Cheong hey..so I'm assuming the x^2 + y^2 =1 circle is one of the Great-Circles of the Unit-Sphere which is why the cone (more specifically, that big isosceles triangle inside a cone) is inscribed within that circle. But since our sphere has a volume of 1, radius of that circle should be the cube root of (3/4π). But the equation of the circle says It's radius is 1. Can you please tell me if my assumption is correct. Thanks in anticipation.

Todd Diez - 1 month, 2 weeks ago

unit sphere means a sphere with radius 1.

Unit sphere does not mean that its volume is 1.

Pi Han Goh - 1 month, 2 weeks ago

Oh okay thank you. A 'sphere of unit volume' and a 'Unit Sphere' is the same thing right?

Todd Diez - 1 month, 2 weeks ago

@Todd Diez – no.

Unit volume = volume of numerical value of 1

Unit sphere = a Sphere where a radius of 1.

Pi Han Goh - 1 month, 2 weeks ago

Argh... Unit volume... noooooooooooooooooooooooo....

Julian Poon - 5 years, 10 months ago

Yesssssssssssssss, the problem writer should have been more specific.

Chew-Seong Cheong - 5 years, 10 months ago

Rocco Dalto
Sep 21, 2016

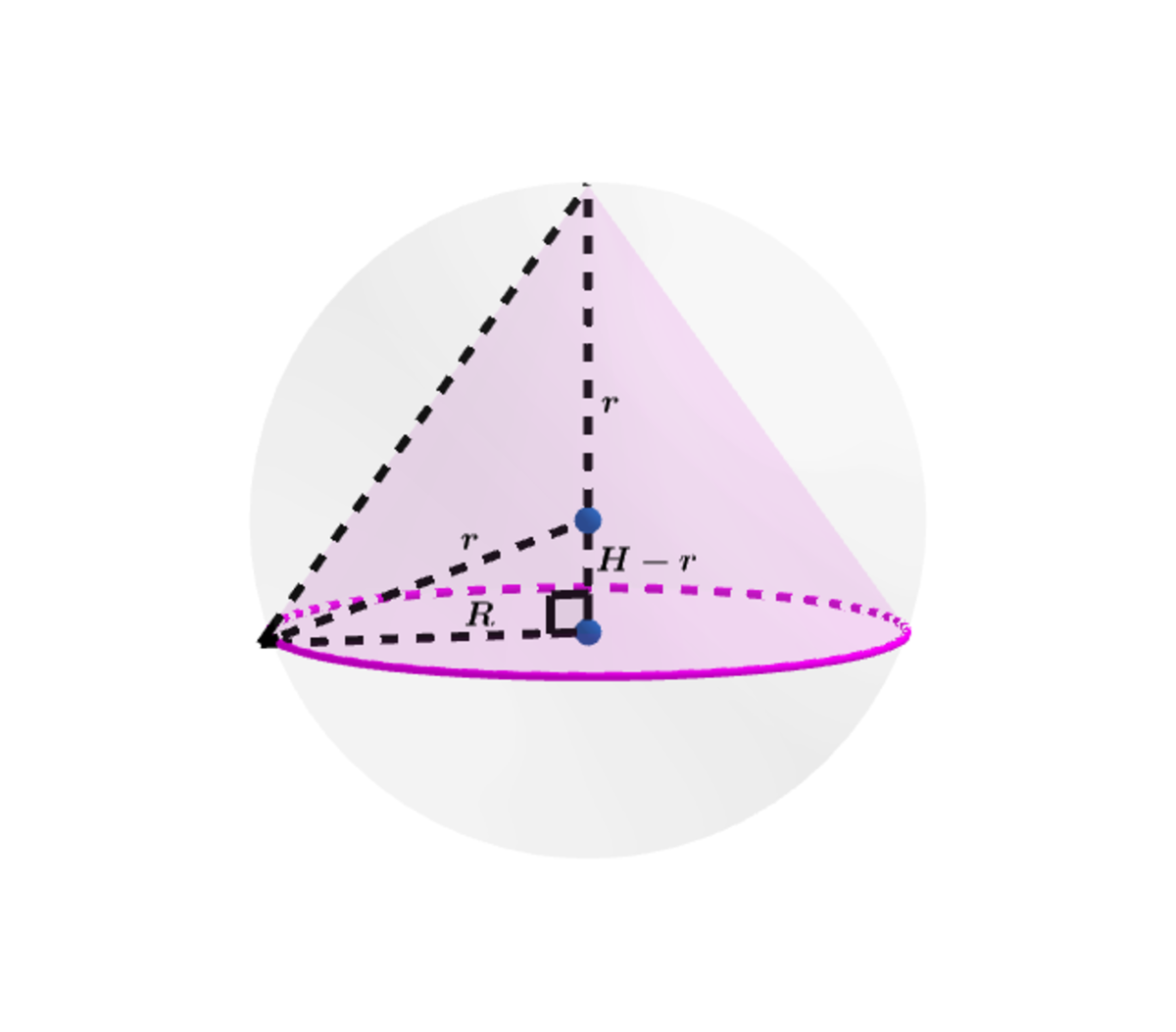
Let the volume of the sphere ${\bf V_{s} = \frac{4}{3} \pi r^3 }$ and the volume of the cone ${\bf V_{c} = \frac{1}{3} \pi R^2 H. }$

From the geometry of the problem we have a right triangle with hypotenuse $r$ and legs $R$ and $H - r$

$\implies R^2 = r^2 - (H - r)^2 \implies V_{c} = \dfrac{1}{3} \pi * (2H^2r - H^3) \implies$

$\dfrac{dV_{c}}{dH} = \frac{1}{3} H \pi * (4r - 3H) = 0$ and $H \neq 0 \implies H = \dfrac{4r}{3}$

$\implies R^2 = \dfrac{8r^2}{9} \implies R = \dfrac{2\sqrt{2}r}{3}$

$\dfrac{d^2V_{c}}{dH^2}|_{H = \dfrac{4r}{3}} < 0 \implies$ max at $H = \dfrac{4r}{3}$

$\therefore V_{c} = (\dfrac{4}{3} \pi r^3) * \dfrac{8}{27} = V_{s} * \dfrac{8}{27}$

Since we have a unit sphere $\implies V_{s} = 1 \implies V_{c} = \dfrac{8}{27} = \dfrac{a}{b} \implies \boxed{a + b = 35}.$

Cone you sphere the time to solve this?

The answer is 35.

2 solutions

Moderator note:

1 pending report

Vote up reports you agree with