Cones and Sphere Geometry Problem
Three identical cones each have a radius of 50 and a height of 120. The cones are placed such that their circular bases touch one another. Then a sphere is placed such that it rests in the space created by the three cones, as shown.
If the top of the sphere is the same height as the top of the cones, what is the radius of the sphere to three decimal places?
The answer is 38.49001795.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution! +1
I don't get it
I tried to simplify the problem by going in only two dimensions, and my assumption was wrong because the radius ended up being r = 33.(3) I am curious now why does my model with two isoscele triangles holding up a circle is not the same as 3 cones holding up a sphere. Hmm... interesting.
Will look at your solution later.
EDIT: I see now, I presumed BD to be 0. That's what happens in two dimensions, the triangles touch bases. In 3 dimensions the bases don't touch in one point. Are you sure this problem is intermediate? I saw advanced problems on this site that were easier than his one.
Log in to reply
I did not set this. The administrators did. I personally think that this would end up on the advanced section. Maybe you should contact the staff.
Log in to reply
Probably too late now in production, but I hope the brilliant staff sees this and takes notes. BTW, brilliant staff: Why don't we have discussions like these under course problems/topics? It seems absurd to me that only weekly problems have comments.
I have just posted what amounts to a two-dimensional solution.
Can it be more simplified??
Log in to reply
Not that I know of
The three solid cones define an interior space in the shape of an inverted (virtual) cone, the same shape at the solid cones - just larger - in which the sphere is contained. The horizontal distance from the tip of a solid cone to the top of the sphere is 100√3/3, or 2√3/3 times the size of the solid cones.
The 2-dimensional representation of this cone and sphere is an (inverted) isosceles triangle with inscribed circle. The dimensions of the triangle are larger than the solid cones by the scaling factor shown above: 200√3/3 base and 260√3/3 equal legs.
Use the formula for the radius of a circle inscribed in an isosceles triangle to obtain the answer of 200√3/9 ≈ 38.049.
I do not understand why the problem cannot be simplified into a 2D situation. The bases in the 3D problem still touch each other, same as it you simplify it into 2 dimensions.
Then, if the bases of the two isosceles triangles are touching, the problem can be even more simplified: the circle would fit the lower part of one of the triangles, leading into a 1circle+1triangle situation instead of 3 cones and 1 sphere.
Please point out my mistake because obviously there must be one, since I didn’t come to the same results.
Log in to reply
When viewing the cones and the sphere from the side, such that the bases of the two cones (seen as isosceles triangles) are just touching each other in the middle, some people are mistakenly assuming that the sphere is tangent to both isosceles triangles, like in Picture #1. However, since the sphere sits in the middle of three cones, the side view looks more like Picture #2, where the sphere is not tangent to both isosceles triangles but overlaps behind the isosceles triangles. The correct side view that shows the sphere tangent to one of the isoscles triangles is in Picture #3, where you are viewing it in such a way that two of the cones are overlapping each other (in the picture, the two overlapping cones are on the left, and the tangent cone is on the right).
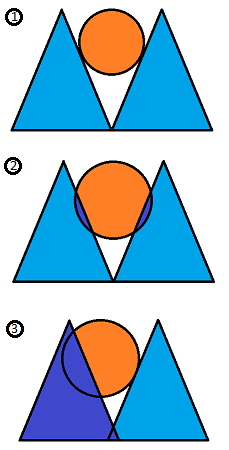
Log in to reply
Oh so true, now I get it, thanks a lot!! I suspected something similar after posting my quiestion, but I didn't know exactly my mistake.
Thank you!
there is a simpler way to reach the result.
can i post a pic here??
Log in to reply
If you got the problem right, then you can add your own solution by clicking the "Discuss Solution" button and filling in the "Add your own solution" form found between the problem and other people's solutions. You can add your own picture by clicking on the picture button just above the form, third from the left.
If you got the problem wrong, then you can't add your own solution, you can only comment on other people's solutions. If you want to add a picture to a comment, there is a work-around - you can go to a completely different problem in the past that you got right and haven't written a solution to yet, and write out your comment (and picture) in the "add your own solution" box there, and even preview it there, but instead of posting it, copy and paste the text (including the code for the picture) into the comment area in the problem you want to comment on.
Log in to reply
I've never heard of that work-around before. Clever!
Thank You. Here it is: This felt simpler to me. God knows what i had been thinking at time of solving this problem.. submitted all the 3 trials.. wrongly.. bad of me... silly mistake during the last trial.
Log in to reply
@Ananya Aaniya – Elegant solution! Too bad you got can't submit this as your own solution so people can upvote it. Thanks for sharing!
Log in to reply
@David Vreken – If anyone can post it as a separate solution , so that people may reach it.. for easy understanding... it will be great. [It will be nice if the person can mention me somewhere.. :D :P ]
Log in to reply
@Ananya Aaniya – I worked it very similar to this (my pictures were almost identical) but just used descriptive geometry without any trig (which made some of my numbers similar to David Vreken's but without using similarity). (I did have to work it a second time because the first time I thought the cone had a diameter of 50 rather than a radius of 50.)
i was like 30? 60? 20? but then it was like NOPE ITS 38.49001795.
notready4math
Great problem. I really had to think about this one. Great solution. I resorted to trig.
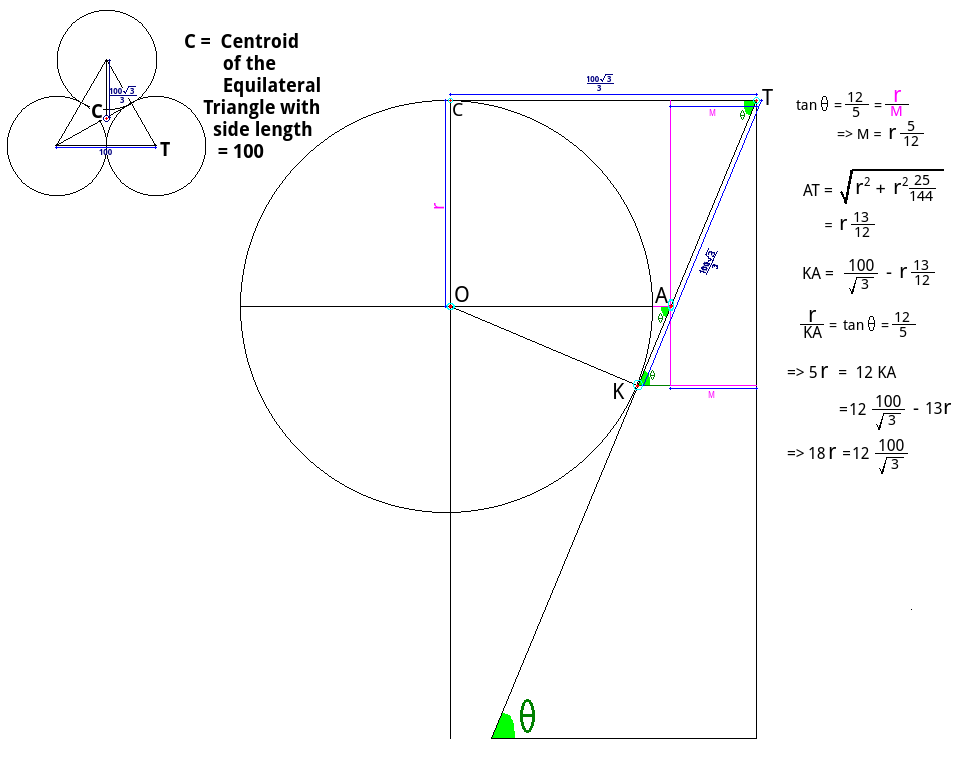
DG is equal to the radius of the circle in which an equilateral triangle with the side length of 100 is inscribed, so DG = 100√3 / 3. Since DG and AB are parallel, <GDF ≡ <DAB ≡ <DBA. Let [BH be the angle bisector of <DBA, where H is on DC, so <CBH ≡ <DBH. Since DG and DF are tangents drawn form D to the circle with center E, <GDE ≡ <FDE. From these we deduce that <GDE ≡ <CBH. Let this angle be α. Using Pythagoras’ theorem in ∆BCD, we obtain BD = √(502 + 1202) = 130. Using the angle bisector theorem, we deduce that CH / DH = BC / BD = 5 / 13. Hence CH / CD = 5 / 18, so CH = 100 / 3. Thus tg α = CH / CB = 2 / 3 = GE / GD = R / (100 / √3), so R = 200√3 / 9 ≈ 38.49
Log in to reply
I want to add a picture, but I couldn't insert it. D is the apex of one cone, DA is the generatrix of that cone which is tangent to the sphere, B is the diametral opposite of A on the base of that cone, C is the center of that base, E is the center of the sphere, F is the point of tangency between that cone and the sphere, G is the uppermost point on the sphere, so DG is parallel to AB and H is the point of intersection between DC and the angle bisector of DBC.
This is a great solution!
Log in to reply
David - You are so adept at creating figures, would you mind posting one for this solution, to save some of the rest of us the trouble of drawing our own? Many thanks!
Log in to reply
Thank you!!
This is simpler... !! :)
This looks to be a Level 3 problem instead.
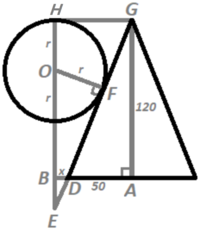 We could find the length of
E
H
by
G
H
=
3
1
0
0
and
△
A
D
G
∼
△
H
G
E
.
Then we could solve
r
by
△
A
D
G
∼
△
O
F
E
,
so there's no need for the length of
B
D
.
We could find the length of
E
H
by
G
H
=
3
1
0
0
and
△
A
D
G
∼
△
H
G
E
.
Then we could solve
r
by
△
A
D
G
∼
△
O
F
E
,
so there's no need for the length of
B
D
.
The three solid cones define an interior space in the shape of an inverted (virtual) cone, the same shape at the solid cones - just larger - in which the sphere is contained. The horizontal distance from the tip of a solid cone to the top of the sphere is 100√3/3, or 2√3/3 times the size of the solid cones.
The 2-dimensional representation of this cone and sphere is an (inverted) isosceles triangle with inscribed circle. The dimensions of the triangle are larger than the solid cones by the scaling factor shown above: 200√3/3 base and 260√3/3 equal legs.
Use the formula for the radius of a circle inscribed in an isosceles triangle to obtain the answer of 200√3/9 ≈ 38.049.
38.049 or 38.49???
It should be 38.49.
Below is a top view of the bases of the three cones, where A is the center of one of the circular bases with radius 5 0 , B is the center between all three cones, D and C are intersection points of the segments and circle A , and x is the length between B and D .
Since the triangle formed by the three circular bases is an equilateral triangle, △ A B C is a 3 0 - 6 0 - 9 0 triangle, and since A C is 5 0 , A B is 3 1 0 0 3 , and since A D is 5 0 , B D = x = 3 1 0 0 3 − 5 0 .
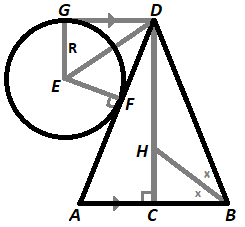
Now this is a side view of one of the cone and sphere, where A , B , D , and x are the same as above, E is the intersection point of the extension of the side of the cone and the line through the sphere perpendicular to the floor, F is the point of tangency between the sphere and the side of the cone, G is the top of the cone, and r is the radius of the sphere:
Then G D = 5 0 2 + 1 2 0 2 = 1 3 0 by Pythagorean's Theorem, and △ A D G ∼ △ B D E ∼ △ F O E by angle-angle similarity.
Since △ A D G ∼ △ B D E , 1 2 0 B E = 5 0 x , so B E = 5 1 2 x .
Since △ A D G ∼ △ F O E , 1 3 0 O E = 5 0 r , and since O E = O B + B E , 1 3 0 5 1 2 x + 1 2 0 − r = 5 0 r , so r = 3 2 x + 1 0 0 = 3 2 ( 3 1 0 0 3 − 5 0 ) + 1 0 0 = 9 2 0 0 3 ≈ 3 8 . 5
Addition: When viewing the cones and the sphere from the side, such that the bases of the two cones (seen as isosceles triangles) are just touching each other in the middle, some people are mistakenly assuming that the sphere is tangent to both isosceles triangles, like in Picture #1. However, since the sphere sits in the middle of three cones, the side view looks more like Picture #2, where the sphere is not tangent to both isosceles triangles but overlaps behind the isosceles triangles. The correct side view that shows the sphere tangent to one of the isoscles triangles is in Picture #3, where you are viewing it in such a way that two of the cones are overlapping each other (in the picture, the two overlapping cones are on the left, and the tangent cone is on the right).