Confusing Triangles
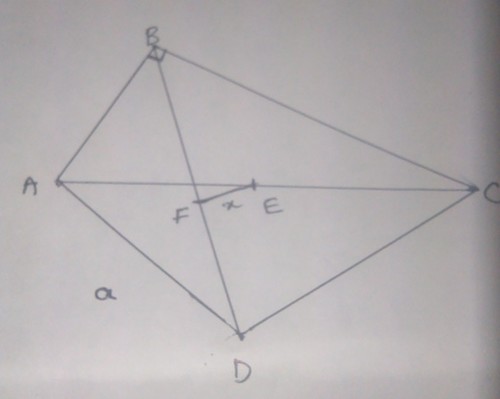In the following figure, ABC is a right angled triangle at B. BDC is an equilateral triangle, E and F are the midpoints of AC and BD respectively, then x=
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
R
i
g
h
t
∠
△
‘
A
B
C
i
s
i
n
c
i
r
c
l
e
A
C
B
w
i
t
h
c
e
n
t
r
e
E
.
R
a
d
i
i
E
B
=
E
C
.
.
.
.
.
.
.
(
1
)
∴
∠
s
E
B
C
=
E
C
B
.
∠
2
=
∠
1
B
u
t
e
q
u
i
v
q
l
e
n
t
△
∠
s
F
B
C
=
G
C
B
.
∠
(
2
+
4
)
=
∠
(
1
+
3
)
∴
a
n
g
l
e
s
F
B
E
=
E
C
G
.
∠
3
=
∠
4
.
.
.
.
.
(
2
)
D
r
a
w
E
G
∥
t
o
A
D
.
∴
E
G
=
a
/
2
.
.
.
.
(
3
)
F
a
n
d
G
a
r
e
m
i
d
p
o
i
n
t
s
o
f
e
q
u
i
v
q
l
e
n
t
△
s
i
d
e
s
∴
F
B
=
G
C
.
.
.
.
.
(
4
)
F
r
o
m
(
1
)
,
(
2
)
a
n
d
(
4
)
△
s
E
F
B
,
E
G
C
a
r
e
c
o
n
g
r
u
e
n
t
.
∴
‘
f
r
o
m
(
3
)
E
F
=
E
G
=
a
/
2
.
D has been shown in the sketch as NOT on circle ABC, nor the proof assumes this.
I guessed right, very easy to see
nice solution
But Question does not mention the problem that all points A,B,C & D are lying on the circumference of a circle.With your expalanations,value of X is surely a/2.Thanks. K.K.GARG,India
Log in to reply
It can be inferred that ABCD is a cyclic quadrilateral.
Since ABC is a right angled triangle, AC must be the diameter of the circle, with midpoint E being the centre. As BCD is also an equilateral triangle, point D must lie on the circle as well.
Log in to reply
How did you infer that A B C D is a cyclic quad? E is not the "center of B C D ", but is the midpoint of the line A C .
In fact, if it is a cyclic quad, then we must have ∠ B A C = ∠ B D C = 6 0 ∘ , which is clearly not necessary.
@Niranjan Khanderia @rugved dhore Thoughts on how to proceed? Is this a necessary assumption?
Log in to reply
@Calvin Lin
–
ABCD is a cyclic quad, only if angle ABC = 60 degrees.
But the proof above does not use the properties of a cyclic quad. It is true without any extra conditions.
So," Challenge Master note:
This solution makes the assumption that is a cyclic quadrilateral, which is not necessarily true."
Does not seem to apply to this proof. Probably it was ment for some othere problem misPostaed here !
Log in to reply
@Niranjan Khanderia – Thanks for clarifying. I read through too quickly, and was misled by the image. I have removed the objection.
Another (now deleted) solution to this problem did make the assumption that ABCD was cyclic.
ya my answer is correct
How did you that you need to draw a circle passing through the points A, B and C? I think, using the strategy you used to solve the question, the problem can be solved without drawing the circle. :)
Since ABC is a right angled triangle, AC must be the diameter of the circle, with midpoint E being the centre. As BCD is also an equilateral triangle, point D must lie on the circle as well.
Log in to reply
D will lie on a circle with A and C, true. But circles ABC and ADC are not the same except when angle ABC = 60 degrees.