Congruent Parts Perimeter
A unit circle is divided into 12 congruent regions, as shown. What is the perimeter of one of these regions?
The answer is 2.838745519.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
As a bonus note, this diagram is based of a problem of the week from two weeks ago.
Doubt in first sentence.
Answer- Let the side which is cut is 'a', i,e which creates a gap in each of those radie be 'a'. Let b=2πr Now perimeter will be 2a+a+(b÷6)+(b÷12). This. 2a+a is due to symmetry, can be checked by visual inspection also.
What about this?
This is wrong, as is "Brilliant" and everyone else - the correct answer is: "Unknown and cannot be solved unless given D [or r] and the units that D is expressed in, OR unless allowed to express the answer in terms of both Pi and D; And, since the puzzle specifically prohibits you from giving an answer in terms of either Pi or D, let alone both (it requires a decimal number and nothing else, without specifying units), that makes the answer by default 'Unknown and cannot be solved'. First you said: "The longer arc must be 1/6 of the circumference of the unit circle, that is Pi/3". Wrong. It is Pi D/6. Why would you assume D=2 (that r=1)? Then you said "From symmetry, the shorter arc must be 1/2 of that, or Pi/6" - again, wrong; the answer is Pi D/12 or Pi*r/6 - why are you leaving out the critical r? I don't get it. With that failed premise, nothing which you build on beyond that matters.
Log in to reply
Doesn't the question specify that it is a unit circle, so we know r? Or was this a later edit?
Log in to reply
It was not a later edit. I am guessing people just missed it.
Exactly my thoughts. We don't know the radius and the question does not specify it is a unit circle. It is unsolvable unless expressed with respects to a parameter r
Log in to reply
I'm guessing you just missed it - The first three words of the problem state "A unit circle".
The problem specifies that we have a unit circle, which by definition has radius 1.
I don't get it why r u being so harsh and saying "This is wrong, as is "Brilliant" and everyone else" when it's your own mistake!!!!Duh!!
Log in to reply
@ Erica Phillips - This is not texting. Spell out your words.
Log in to reply
@Dennis Rodman – It doesn't hurt until u understand
Please clarify that it's the unit circle, thanks ^^
Aren't you assuming GF is bisected? I don't see how you can provide that
I suggest that this problem should be better located in "Advanced."
Relevant wiki: Length and Area - Composite Figures - Intermediate
Due to symmetry, the length of the longer arc is 6 1 the circle's circumference, and the shorter arc is 2 1 of that.
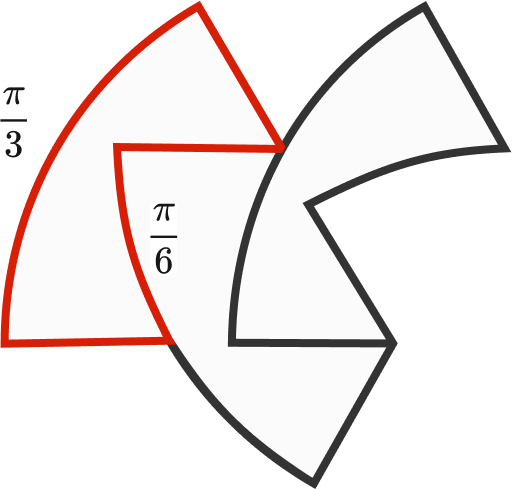
Also due to symmetry, each of the segments in the figure has the same length. Call this length x . We can extend some segments and connect some points to form a rhombus.
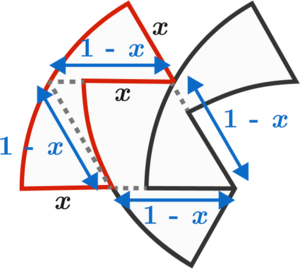
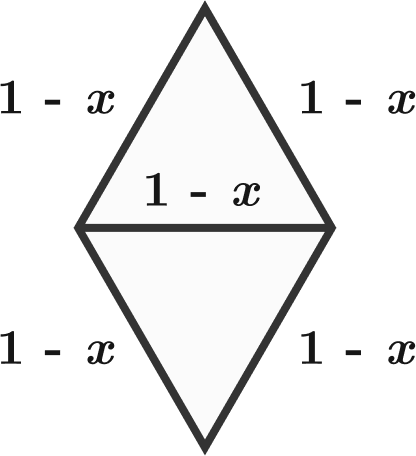
Note that the longer diameter of the rhombus is the circle's radius. Making use of special triangle relationships, we have
3 ( 1 − x ) x = 1 = 1 − 3 3
Summing the arc lengths and 3 x gives 3 − 3 + 2 π ≈ 2 . 8 3 9 .
Hey, quick question, how can we be sure that the smaller arc is 1/2 of the bigger one?
Log in to reply
Look here:
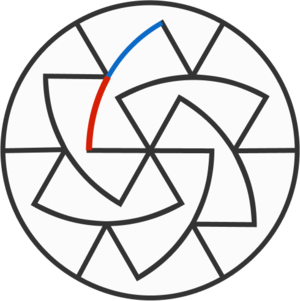
The blue and red arcs are both smaller arcs in different parts, and they are both part of a larger arc in another part.
Can please explain the special trinagle relationship or please provide the source to it thank you
Log in to reply
Special triangles are right triangles that have angle measurements 45-45-90 or 30-60-90 (in degrees). See here for more information.
Thanks Andrew
First, draw line from A to B . If the radius of the circle is 1 , then P Q = A B = 1 also, so that A C = 2 1 .
From this, we can find A P = 3 1 , so that Q A = 1 − 3 1
Then the perimeter of each piece is
( 1 + 2 1 ) ( 6 1 ) 2 π + 3 ( 1 − 3 1 ) = 2 . 8 3 8 7 5
Look for (or imagine)
6
1
of radius
1
circle pizza slices to see how
P
Q
=
A
B
=
1
and
A
C
=
2
1
A
B
Consider those pieces that include points
P
and
A
as the center of their arcs.
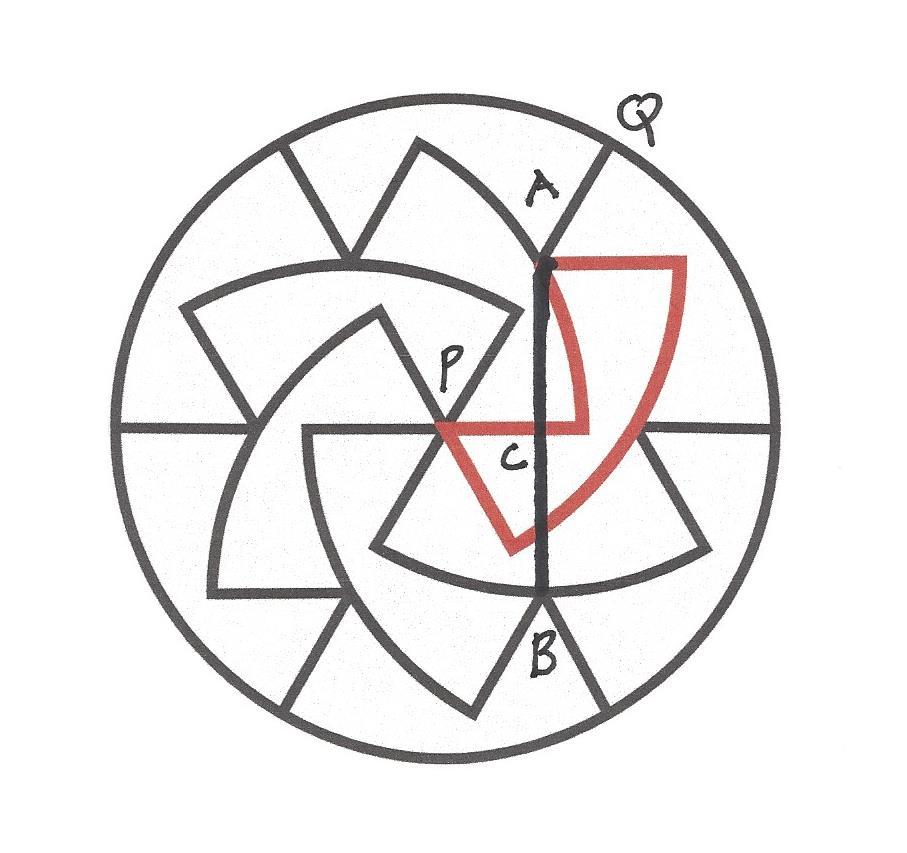
How do you know AB is 1 and AC 1/2?
Log in to reply
See my added comments. A B = P Q = 1
Log in to reply
Ok, I can see AB = PQ, but I still don't see how to know that AC = 1/2AB (plus I dont even see a point labled D on the drawing.)
Log in to reply
@Gustaf Carstam – Fixed! AD changed to AB. Consider the symmetry of the figure, above and below the horizontal diameter of the circle. I could draw in more lines, but I was afraid that would only confuse things more.
Try to look past the flower in the center, which could be confusing things for you. Just look at the 6 basic pizza slices like how everybody slices pizza.
Relevant wiki: Length and Area - Composite Figures - Intermediate
The longer arc must be 6 1 of the circumference of the unit circle, that is 3 π .
From symmetry, the shorter arc must be 2 1 of that or 6 π , since G B must be equal to B F .
To get lengths of the three identical straight segments, note that the yellow lines must be the same length, as they play the same role in shapes C B E D and C A G F respectively.
The triangle A B C has to be equilateral, so A H = H I = 2 1 .
This gives us A B = 3 1 and B E = 1 − 3 1 .
The final result is then the sum 3 π + 6 π + 3 ⋅ ( 1 − 3 1 ) ≈ 2 . 8 3 8 7 .