Conjugates
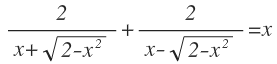Find the INTEGRAL value of x that satisfies this equation.
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
*Integer, * 2 .
Log in to reply
What do you mean? @Dieuler Oliveira
Log in to reply
The irrational root is 2 instead of 3 .
Log in to reply
@Dieuler Oliveira – The equation has three roots: 0, +sqrt(3) and -sqrt(3). The integral is 0.
Log in to reply
@Boryana Atanasova – Ok, I'm wrong. I've calculated it mentally and didn't notice 2 wasn't root. But 0 is the ONLY solution of the equation, since 2 − x 2 ≥ 0 ⇒ − 2 ≤ x ≤ 2
Since the denominator is conjugates, neither the sum nor the product will contain radicals. By clearing out the fractions (with common denominators) we get 4x=2x(x^2-1) which leaves us with x=0 or x=square root of 3. The only integral value is 0.