Connect the curve 2
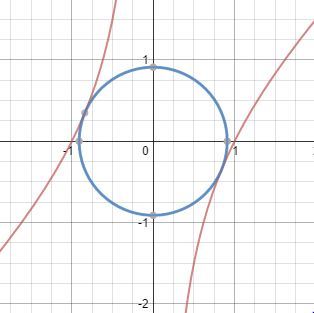 The figure shows the graph of
f
(
x
)
=
x
−
x
1
.
The figure shows the graph of
f
(
x
)
=
x
−
x
1
.
The circle is tangent to the graph in domain x < 0 and x > 0 , and is the smallest of its kind.
The area of the circle is in the form A π ( − B + C ) where A , B , C are positive integers with C square free.
Find A + B + C .
More problems like this .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
another way to solve this problem is to find the smallest value of radius so we get
r 2 = ( x − x 1 ) 2 + x 2
and condition is d x d r = 0
0 = d x d ( 2 x 2 + x 2 1 − 2 ) = 4 x − x 3 2
then x = ± 2 4 1
substitute this value into radius square expression
r 2 = 2 2 − 2
then area is equal to
2 π ( − 1 + 2 ) = A π ( − B + C )
thus A + B + C = 2 + 1 + 2 = 5
f ( x ) has rotational symmetry about the origin and so the circle is centred at the origin.
To find where the circle and the function intersect we have to solve the simultaneous equations
y = x + x 1
x 2 + y 2 = r 2
Squaring the first of these and substituting into the second gives
x 2 + ( x − x 1 ) 2 = r 2
⟹ x 2 + ( x 2 − 2 + x 2 1 ) = r 2
⟹ 2 x 4 − ( 2 + r 2 ) x 2 + 1 = 0
We can interpret this as a quadratic equation in x 2 . Because we are looking for points of tangency we want it to have exactly one solution for x 2 (which will yield two solutions for x , one positive and one negative). So the discriminant of the equation must be zero, in other words
( 2 + r 2 ) 2 − 8 = 0
⟹ r 2 = 2 2 − 2 = 2 ( − 1 + 2 )
The required area is thus 2 π ( − 1 + 2 )
and so A + B + C = 2 + 1 + 2 = 5
I guessed that you want A + B + C.
Similar to the last connect the curve posted where the curve was y=x+1/x.The same fundamental applies here as the function being odd is symmetric in opposite quadrant(i.e about origin)
I got answer by using simple Tangent normal ........
But can anyone explain me why Symmetry Don't works here ...?
Since due to symmetry isn't it is obevious that y = − x is common normal to them Beacuse y = x is assymptot of Curve-1 , Hence simply substitute it in curve-1 , i.e − x = x − 1 / x which gives x = 1 / s q r t ( 2 ) Hence radius is 1 , which contradicts ....
Log in to reply
Yes y=-x is common normal but you need to check that does the curve, circle and line meet at a single point (it doesn't in this case).
Log in to reply
sorry .. i didn't understand ..
u r agree it is common normal , then isn't it obvious that they meet at same point (2 times )... Please explain more ............
Log in to reply
@Karan Shekhawat – Have you checked that the curve and circle are tangent for r = 1 ? If you'll sketch the graph they intersect at 4 points.
@Archit Boobna It isn't Level 5.
Log in to reply
What isn't level 5?
Let the equation of the circle be x 2 + y 2 = r 2 . Where, r is the radius of the circle. Then, we have:
2 x + 2 y d x d y = 0 ⇒ d x d y = − y x
f ( x ) = y = x − x 1 ⇒ d x d y = 1 + x 2 1
At the tangent points,
− y x = 1 + x 2 1 ⇒ − x = ( 1 + x 2 1 ) y ⇒ − x = ( 1 + x 2 1 ) ( x − x 1 )
⇒ − x = x − x 1 + x 1 − x 3 1 ⇒ x 3 1 = 2 x ⇒ x 4 = 2 1 ⇒ x 2 = 2 1
y = x − x 1 ⇒ y 2 = ( x − x 1 ) 2 = x 2 − 2 + x 2 1 = 2 1 − 2 + 2
r 2 = x 2 + y 2 = 2 1 + 2 1 − 2 + 2 = 2 2 − 2
The area of the circle is given by: π r 2 = π ( 2 2 − 2 ) = 2 π ( − 1 + 2 ) .
⇒ A + B + C = 2 + 1 + 2 = 5
The graph to confirm the answer is as follows: