Connect the curve 4
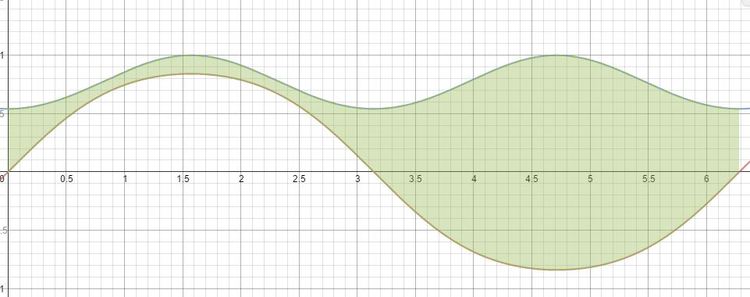 The figure shows the curves of
y
=
cos
(
cos
(
x
)
)
in blue and
y
=
sin
(
sin
(
x
)
)
in red.
The figure shows the curves of
y
=
cos
(
cos
(
x
)
)
in blue and
y
=
sin
(
sin
(
x
)
)
in red.
It also shows a green region enclosed between these graphs in domain [ 0 , 2 π ] .
If the area of the green region is A π B J α ( n )
Find A + B + α + n
Details and Assumptions
- J α ( n ) is a Bessel function of the first kind.
Or J α ( n ) = m = 0 ∑ ∞ m ! Γ ( m + α + 1 ) ( − 1 ) m ( 2 n ) 2 m + α
-
A , B , α and n are integers.
-
α < n
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is the first time I'm seeing a solution of yours . Nicely done!
@Calvin Lin
@Archit Boobna
How to evaluate
∫
0
π
c
o
s
(
c
o
s
x
)
d
x
without using W|A.
Log in to reply
Since it is already mentioned in the question that the answer has to mentioned in terms of bessel function, it can be done easily.
Actually this integral can't be expressed normally.
2 basic ways are that J0(1) is one of the most well know bessel function, one may know that π 1 ∫ 0 π cos cos x d x = J 0 ( 1 )
or it may be known that π 1 ∫ 0 π cos ( n cos x ) d x = J 0 ( n ) which can directly lead to the answer, if one doesnt know these, then I am not sure how he'll do it..
Maybe it can be done by immense calculus , and by using the summation.
I think there is a typo in your solution.
Why have you multiplied Area(1) and Area(2)
@Calvin Lin , Sir I want to take a screenshot of a moving desmos graph on my windows 8 laptop so that I can post it in my next question. Can you tell me how to save a screenshot as GIF? Thanks.
Log in to reply
If you send me the link of the graph I can help you.
Log in to reply
I will send you when I will make it.
Log in to reply
@Archit Boobna – Are you sending me the link ?
Log in to reply
@Rajdeep Dhingra – Yes wait I am sending
@Rajdeep Dhingra – https://www.desmos.com/calculator/n7ifsogxqw
I used the Residue theorem.
The area is A = ∫ 0 2 π ( cos ( cos ( x ) ) − sin ( sin ( x ) ) ) d x . . . (i)
Using the property ∫ a b f ( x ) d x = ∫ a b f ( a + b − x ) d x ,we get
A = ∫ 0 2 π ( cos ( cos ( x ) ) + sin ( sin ( x ) ) ) d x . . . (ii).
Adding (i) and (ii), we get A = ∫ 0 2 π cos ( cos ( x ) ) d x
Now take z = e i x and i z d z = d x
A = ∮ cos ( 2 z + ( 1 / z ) ) i z d z = i 1 ∮ z 1 cos ( 2 z z 2 + 1 ) d z
The contour is the unit circle centred at the origin and is traversed in the counterclockwise (anticlockwise) direction.
There is only one pole of the integrand inside this contour, namely 0.
Hence we find the residue of the integrand z 1 cos ( 2 z z 2 + 1 ) at z = 0 .
We know that the residue at a point c is the ( z − c ) − 1 coefficient in the laurent series about that point
Writing down the laurent series of the integrand about 0, we find the z − 1 coefficient (i.e. the residue) to be
m = 0 ∑ ∞ 2 2 m ( 2 m ) ! ( − 1 ) m ( m 2 m )
= m = 0 ∑ ∞ 2 2 m ( m ! ) ( m ! ) ( − 1 ) m
= m = 0 ∑ ∞ m ! Γ ( m + 0 + 1 ) ( − 1 ) m ( 2 1 ) 2 m + 0
= J 0 ( 1 )
Hence by the residue theorem,
A = i 1 2 π i ( z 0 ∈ P ∑ R e s z = z 0 ( z 1 cos ( 2 z z 2 + 1 ) ) ) where P is the set of all poles inside the contour
A = 2 π R e s z = 0 ( z 1 cos ( 2 z z 2 + 1 ) ) = 2 π J 0 ( 1 )
So finally we have A = 2 , B = 1 , α = 0 , n = 1
A + B + α + n = 4
You sir, are a genius.

Let the Green shaded Region's Area be A
A = Area(1) - Area(2) + Area(3) - Area(4) (There is a -ve sign before Area(4) as it is negative but we need to add it.)
We can rewrite this as
A = ∫ 0 π c o s ( c o s x ) d x − ∫ 0 π s i n ( s i n ( x ) ) + ∫ π 2 π c o s ( c o s ( x ) ) d x − ∫ π 2 π s i n ( s i n x ) d x
Changing limits of the integrals we get
A = ∫ 0 π c o s ( c o s x ) d x − ∫ 0 π s i n ( s i n ( x ) ) + ∫ 0 π c o s ( c o s ( x ) ) d x + ∫ 0 π s i n ( s i n x ) d x
Simplifying we get
A = 2 ∫ 0 π c o s ( c o s x ) d x
Hence
A = 2 π J α ( n )